List of Figures

1. Fundamental questions in multiserver systems.
2. An example of Markov chain modeling: an M/M/1/FCFS queue.
3. A 1D Markov chain.
4. A multidimensional Markov chain that appears in a multiserver analysis.
5. Organization of Part I: Analytical tools for multiserver systems.
6. The key idea in DR: dimensionality reduction (2D $\rightarrow$ 1D).
7. Organization of Part II: Performance analysis of multiserver systems.
8. The SBCS-ID policy.
9. The SBCS-CQ policy.
10. A threshold-based policy for reducing switching costs in cycle stealing.
11. The Beneficiary-Donor model.
12. A PH distribution as the distribution of the time until absorption in a continuous time Markov chain.
13. The Markov chain whose absorption time defines an $n$-phase EC distribution.
14. The Markov chain whose absorption time defines an extended EC distribution.
15. Set ${\cal T}^{(n)}$ as a function of the normalized moments.
16. Characterizing 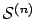${\cal S}^{(n)}$ via ${\cal T}^{(n)}$.
17. Examples of PH distributions.
18. A three-phase PH distribution.
19. Subclasses of the PH distribution.
20. Set ${\cal S}^{(2)}$ and set ${\cal S}^{(2)^*}$.
21. A classification of distributions.
22. An implementation of the Simple closed form solution.
23. Ideas in the Simple solution.
24. An implementation of the Complete closed form solution.
25. Ideas in the Complete solution.
26. An implementation of the Positive closed form solution.
27. Ideas in the Positive solution.
28. Examples of multidimensional Markov chains that model multiserver systems.
29. Markov chains for an M/M/2 queue with two preemptive priority classes.
30. Dimensionality reduction of 2D Markov chain.
31. Markov chains for an M/PH/2 queue with two preemptive priority classes.
32. Markov chain on a finite state space for the high priority jobs in an M/PH/2 queue with two preemptive priority classes.
33. 1D Markov chain for an M/PH/2 queue with two preemptive priority classes.
34. FB, RFB, and GFB processes.
35. Examples of QBD processes.
36. Examples of Markovian arrival processes.
37. QBD processes for MAP/M/1 queues.
38. A MAP(2)
39. Algorithms for calculating $\mathbf{R}$, $\mathbf{R}^{(\ell)}$'s, and other relevant matrices.
40. FB process consisting of a foreground birth-and-death process and a background birth-and-death process.
41. An example of an RFB process: Size-based task assignment with cycle stealing under immediate dispatching.
42. Ideas in the RFB process.
43. An example of an RFB process: Preemptive priority queue.
44. The structure of the GFB process.
45. An example of an GFB process: Threshold-based policy for reducing switching costs in cycle stealing.
46. An example of a GFB process: Size-based task assignment with cycle stealing under central queue.
47. An example of a GFB process: Nonpreemptive priority queue.
48. Threshold-based policies for the Beneficiary-Donor model.
49. Examples of GFB processes: Threshold-based policies for the Beneficiary-Donor model.
50. An analysis of the FB process in Figure 3.13 via DR.
51. An analysis of the GFB process via DR.
52. A GFB process: Threshold-based policy for reducing switching costs in cycle stealing.
53. An analysis of the GFB process in Figure 3.25 via DR.
54. Background processes on a finite state space, obtained via DR-PI and DR-CI.
55. Markov chains whose stationary probabilities are computed via DR in the analysis of an M/M/2 queue with two preemptive priority classes.
56. Markov chains used to compute the response time in an M/M/2 queue with two preemptive priority classes.
57. Accuracy of DR in the analysis of preemptive priority queues.
58. Accuracy of DR, DR-PI, and DR-CI in predicting the first two moments of the queue length distributions.
59. Accuracy of DR, DR-PI, and DR-CI at different loads.
60. Accuracy of DR, DR-PI, and DR-CI at different job size configurations.
61. Error in DR, DR-PI, and DR-CI when the busy period is approximated by an exponential distribution matching only the first moment.
62. Running time of DR, when applied to an analysis of the preemptive priority queue.
63. Running time of DR, DR-PI, and DR-CI, when applied to an analysis of SBCS-ID.
64. How many servers are best in a single server (FCFS) system?
65. How many servers are best when the two priority classes have the same mean job size?
66. How many servers are best when the high priority jobs have a smaller mean job size?
67. How many servers are best when the high priority class has a larger mean job size?
68. Mean response time as a function of the number of servers.
69. Comparison of DR with BB with respect to the question of ``how many servers are best?''
70. Comparison of DR-A, MK-N, and BB approximations for M/PH/2 with 4 priority classes.
71. Size-based task assignment with cycle stealing.
72. Stability region for Dedicated, SBCS-ID, and SBCS-CQ.
73. Mean response time of short jobs and long jobs under Dedicated, SBCS-ID, and SBCS-ID.
74. Percentage change in the overall mean response time of SBCS-ID and SBCS-CQ against Dedicated.
75. Effect of variability in long job size on the mean response time.
76. A threshold-based policy for reducing switching costs in cycle stealing.
77. A renewal cycle of the donor queue under the threshold-based policy for reducing switching costs in cycle stealing.
78. Stability region for the threshold-based policy for reducing switching costs in cycle stealing.
79. The mean response time for beneficiary jobs and donor jobs as a function of 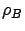$\rho _B$ under cycle stealing and dedicated servers.
80. The gain of beneficiary jobs and pain of donor jobs, and the effect of cycle stealing on the overall mean response time relative to dedicated servers: exponential distributions
81. The gain of beneficiary jobs and pain of donor jobs, and the effect of cycle stealing on the overall mean response time relative to dedicated servers: PH distribution.
82. The impact of the variability of donor job sizes on the mean response time of the beneficiary jobs.
83. The mean response time for beneficiary jobs and donor jobs as a function of $\rho _B$.
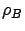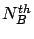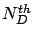84. Optimal values of $N_B^{th}$ and $N_D^{th}$ with respect to overall mean response time.
85. The Beneficiary-Donor model.
86. The T1 policy and the T2 policy.
87. Stability conditions for the T1 policies and for the T2 policy.
88. The mean response time under the T1 policy as a function of $T_1$ and the mean response time under the T2 policy as a function of $T_2$, when $c_1\mu _{12}=c_2\mu _2$.
89. The mean response time under the T1 policy as a function of $T_1$, and the mean response time under the T2 policy as a function of $T_2$, when $c_1\mu _{12}> c_2\mu _2$.
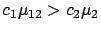90. Static robustness of single-threshold allocation policies.
91. The T1T2 policy.
92. Static robustness of the T1T2 policy.
93. The ADT policy.
94. Static robustness of the ADT policy.
95. Comparison of the ADT policy with the T1 policy with respect to the mean response time.
96. Dynamic robustness of the ADT policy and the T1 policy.
97. Contact center architecture.
98. A flow of routing policy design and capacity management/planning at a contact center.
99. Virtual waiting time analysis.
100. The Markov chain whose absorption time defines an Erlang-Exp distribution.
101. The Markov chain whose absorption time defines an Exp-Erlang distribution.