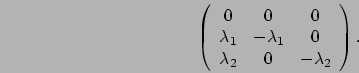We start by providing canonical examples of PH distributions. Here, we provide both pictorial explanation and more formal explanation. Pictorial explanation gives intuitive understanding of the PH distribution, and more formal explanation allows us to get used to the notation that we use later.
First, an exponential distribution is a PH distribution.
Figure 2.6(a) illustrates an exponential distribution
as the absorption time in a (continuous time) Markov chain2.2. At time
0, we start at state 1. We stay in this state for a random time
having an exponential distribution with rate ![]() , and then
transition to state 0, the absorbing state. The time until we enter
the absorbing state is, of course, an exponential distribution. More
formally, an exponential distribution with rate
, and then
transition to state 0, the absorbing state. The time until we enter
the absorbing state is, of course, an exponential distribution. More
formally, an exponential distribution with rate ![]() is the
distribution of the time until absorption into state 0 in a Markov
chain on the states
is the
distribution of the time until absorption into state 0 in a Markov
chain on the states ![]() with initial probability vector
with initial probability vector ![]() and infinitesimal generator:
and infinitesimal generator:

|
Second, a convolution of two independent identical exponential
distributions is a PH distribution (i.e., the sum of two i.i.d. exponential random variables has a PH distribution);
this distribution is called an Erlang-2 distribution.
Figure 2.6(b) illustrates an Erlang-2
distribution as the absorption time in a Markov chain. At time 0, we
start at state 1.
After a random time having an exponential distribution with rate ![]() ,
we transition to state 2.
We stay in state 2 for a
random time having an exponential distribution with rate
,
we transition to state 2.
We stay in state 2 for a
random time having an exponential distribution with rate ![]() ,
and then transition to state 0, the absorbing state. The time until we
enter the absorbing state has an Erlang-2 distribution.
More formally, an Erlang-2 distribution with parameter
,
and then transition to state 0, the absorbing state. The time until we
enter the absorbing state has an Erlang-2 distribution.
More formally, an Erlang-2 distribution with parameter ![]() is the
distribution of the time until absorption into state 0 in a Markov
chain on the states
is the
distribution of the time until absorption into state 0 in a Markov
chain on the states ![]() with initial probability vector
with initial probability vector ![]() and infinitesimal generator:
and infinitesimal generator:

Third, a mixture of two exponential distributions is a PH
distribution; this distribution is called a two-phase hyperexponential
distribution, H![]() . Figure 2.6(c) illustrates an
H
. Figure 2.6(c) illustrates an
H![]() distribution as the absorption time in a Markov chain.
At time 0, we start at state 1
with probability
distribution as the absorption time in a Markov chain.
At time 0, we start at state 1
with probability ![]() and at state 2
with probability
and at state 2
with probability ![]() .
If we start at state 1 (respectively, state 2), we stay there for a random
time having an exponential distribution with rate
.
If we start at state 1 (respectively, state 2), we stay there for a random
time having an exponential distribution with rate ![]() (respectively,
(respectively, ![]() ), and
then transition to state 0, the absorbing state.
The time until we enter
the absorbing state has an H
), and
then transition to state 0, the absorbing state.
The time until we enter
the absorbing state has an H![]() distribution. More formally, an
H
distribution. More formally, an
H![]() distribution with parameter (
distribution with parameter (![]() ,
,![]() ,
,![]() ,
,![]() ) is the distribution of
the time until absorption into state 0 in a Markov chain on the states
) is the distribution of
the time until absorption into state 0 in a Markov chain on the states
![]() with initial probability vector
with initial probability vector
![]() and
infinitesimal generator:
and
infinitesimal generator: