



Next: The MK-N and DR-A
Up: New approximations for many
Previous: New approximation: DR-A
Contents
Comparing DR-A with BB and MK-N
Figure 4.7:
Comparison of DR-A, MK-N, and BB approximations for M/PH/2 with 4
priority classes
with
![$\mbox{{\bf\sf E}}\left[ X_4 \right]=1$](img1284.png) ,
,
![$\mbox{{\bf\sf E}}\left[ X_3 \right]=\alpha$](img1285.png) ,
,
![$\mbox{{\bf\sf E}}\left[ X_2 \right]=\alpha^2$](img1286.png) , and
, and
![$\mbox{{\bf\sf E}}\left[ X_1 \right]=\alpha^3$](img1287.png) , as a function of
, as a function of 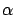 .
Here, the squared coefficient of variability of the job size distributions
are
.
Here, the squared coefficient of variability of the job size distributions
are 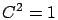 (top two rows) or
(top two rows) or  (bottom two rows) for all classes. Load is balanced among the classes.
Note that MK-N does not appear for
(bottom two rows) for all classes. Load is balanced among the classes.
Note that MK-N does not appear for  ,
because the error is beyond the scale of the graphs for most values of
,
because the error is beyond the scale of the graphs for most values of 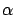 .
.
Comparison of approximations for M/M/2 with 4 priority classes (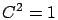 ) )
Comparison of approximations for M/PH/2 with 4 priority classes ( ) )
|
We now evaluate the accuracy of DR-A,
BB, and MK-N. In all figures,
we assume 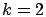 servers and
servers and 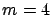 priority classes. We consider
both the case where each priority class has an exponential job
size distribution (
priority classes. We consider
both the case where each priority class has an exponential job
size distribution (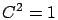 ; top half of Figure 4.7)
and the case of two-phase PH job size distributions with
; top half of Figure 4.7)
and the case of two-phase PH job size distributions with  (bottom
half of Figure 4.7)4.3. Each class may have a
different mean job size, and these are chosen to vary over a large
range, determined by parameter
(bottom
half of Figure 4.7)4.3. Each class may have a
different mean job size, and these are chosen to vary over a large
range, determined by parameter 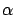 . Specifically, the mean job size of
class
. Specifically, the mean job size of
class  is set
is set
![$\mbox{{\bf\sf E}}\left[ X_i \right]=\alpha^{4-i}$](img1288.png) , where
, where
 . Thus,
. Thus,  implies small high priority jobs. We equalize the load between
the classes, i.e.
implies small high priority jobs. We equalize the load between
the classes, i.e.
 , where
, where  is
the load of class
is
the load of class  . With these settings, the error in mean delay is evaluated for each class of
jobs, where the error of an approximation is defined as follows:
. With these settings, the error in mean delay is evaluated for each class of
jobs, where the error of an approximation is defined as follows:
Thus, positive error means overestimation
and negative error means underestimation of the approximation.
Simulation is kept running until the simulation error becomes less
than 1% with probability 0.95 (see Section 3.9 for
more technical details of our simulation).
In evaluating the BB and MK-N approximations, we use accurate methods
known to compute their components. For example, BB relies on knowing
the mean delay for the M/PH/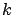 /FCFS queue. We compute this delay
precisely for the PH job size distribution using matrix analytic
methods. MK-N relies on being able to analyze the case of two
priority classes (since
/FCFS queue. We compute this delay
precisely for the PH job size distribution using matrix analytic
methods. MK-N relies on being able to analyze the case of two
priority classes (since 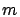 classes are reduced to two). We analyze
the two priority class case in MK-N using DR. We first discuss the accuracy of
MK-N and DR-A, and then discuss the accuracy of BB.
classes are reduced to two). We analyze
the two priority class case in MK-N using DR. We first discuss the accuracy of
MK-N and DR-A, and then discuss the accuracy of BB.
Subsections




Next: The MK-N and DR-A
Up: New approximations for many
Previous: New approximation: DR-A
Contents
Takayuki Osogami
2005-07-19
![]() servers and
servers and ![]() priority classes. We consider
both the case where each priority class has an exponential job
size distribution (
priority classes. We consider
both the case where each priority class has an exponential job
size distribution (![]() ; top half of Figure 4.7)
and the case of two-phase PH job size distributions with
; top half of Figure 4.7)
and the case of two-phase PH job size distributions with ![]() (bottom
half of Figure 4.7)4.3. Each class may have a
different mean job size, and these are chosen to vary over a large
range, determined by parameter
(bottom
half of Figure 4.7)4.3. Each class may have a
different mean job size, and these are chosen to vary over a large
range, determined by parameter ![]() . Specifically, the mean job size of
class
. Specifically, the mean job size of
class ![]() is set
is set
![]() , where
, where
![]() . Thus,
. Thus, ![]() implies small high priority jobs. We equalize the load between
the classes, i.e.
implies small high priority jobs. We equalize the load between
the classes, i.e.
![]() , where
, where ![]() is
the load of class
is
the load of class ![]() . With these settings, the error in mean delay is evaluated for each class of
jobs, where the error of an approximation is defined as follows:
. With these settings, the error in mean delay is evaluated for each class of
jobs, where the error of an approximation is defined as follows:
![]() /FCFS queue. We compute this delay
precisely for the PH job size distribution using matrix analytic
methods. MK-N relies on being able to analyze the case of two
priority classes (since
/FCFS queue. We compute this delay
precisely for the PH job size distribution using matrix analytic
methods. MK-N relies on being able to analyze the case of two
priority classes (since ![]() classes are reduced to two). We analyze
the two priority class case in MK-N using DR. We first discuss the accuracy of
MK-N and DR-A, and then discuss the accuracy of BB.
classes are reduced to two). We analyze
the two priority class case in MK-N using DR. We first discuss the accuracy of
MK-N and DR-A, and then discuss the accuracy of BB.