



Next: Dimensionality reduction with complete
Up: Approximations of dimensionality reduction
Previous: Approximations of dimensionality reduction
Contents
Dimensionality reduction with partial independence assumption
DR-PI (DR with partial independence assumption) ignores the dependency
that the sojourn time in levels 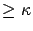 has on how
the Markov chain enters levels
has on how
the Markov chain enters levels 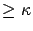 (from level
(from level 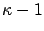 ).
Specifically, we assume that
).
Specifically, we assume that  is independent of
is independent of
 . Let
. Let
 for all
for all  for each
for each 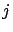 , and let
, and let
 denote the process that is the same as
denote the process that is the same as 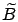 except that
except that  is replaced by
is replaced by  for all
for all  for each
for each 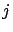 .
Figure 3.27(a) shows the Markov chain for
the high priority jobs (background process) that we obtain via DR-PI in the analysis of an
M/PH/2 queue with two priority classes.
(Recall the Markov chain that we obtain via DR, Figure 3.5 in
Section 3.1, where
the four types of busy periods are
approximated by four PH distributions, respectively.)
In DR-PI, the four types of busy
periods are represented by two PH distributions, ignoring the
dependency that the duration of the busy period has on the phase of
the job in service at the beginning of the busy period.
.
Figure 3.27(a) shows the Markov chain for
the high priority jobs (background process) that we obtain via DR-PI in the analysis of an
M/PH/2 queue with two priority classes.
(Recall the Markov chain that we obtain via DR, Figure 3.5 in
Section 3.1, where
the four types of busy periods are
approximated by four PH distributions, respectively.)
In DR-PI, the four types of busy
periods are represented by two PH distributions, ignoring the
dependency that the duration of the busy period has on the phase of
the job in service at the beginning of the busy period.
Figure 3.27:
Background processes on a finite state space, obtained via (a) DR-PI and (b) DR-CI.
Labels on the transitions in the busy periods are omitted for clarity.
|
|
In general, we require that process  has the following
two key properties:
has the following
two key properties:
- The probability of event
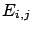 in
in  is the same as that in
is the same as that in  (and that in
(and that in 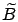 as well).
as well).
- We choose
 such that the marginal distribution of
the sojourn time in levels
such that the marginal distribution of
the sojourn time in levels 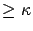 in
in  well-represents that in
well-represents that in  (and hence in
(and hence in 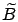 as well).
as well).
Hence,  and
and  would have
stochastically the same total sojourn time in levels
would have
stochastically the same total sojourn time in levels 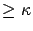 in the long run
if the second property did not involve the approximation (i.e., if the marginal distribution is fitted exactly).
However,
in the long run
if the second property did not involve the approximation (i.e., if the marginal distribution is fitted exactly).
However,
 and
and  have different
autocorrelation in the sequence of the sojourn times in levels
have different
autocorrelation in the sequence of the sojourn times in levels 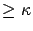 .
.
More formally, the generator matrix
of  ,
,
 , is determined as follows.
Let
, is determined as follows.
Let
 be the
be the  -th moment of
-th moment of  for
for
 for each
for each 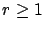 .
We determine
.
We determine
 so that
so that 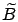 and
and  have
the same marginal
have
the same marginal  -th moment of the sojourn time in levels
-th moment of the sojourn time in levels 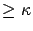 :
:
where
 denotes the stationary probability vector that
denotes the stationary probability vector that 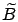 is in level
is in level 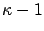 ,
which can be calculated via matrix analytic methods as in Section 3.2.
We approximate
,
which can be calculated via matrix analytic methods as in Section 3.2.
We approximate  by a PH distribution,
by a PH distribution,
 ,
matching the first three moments of
,
matching the first three moments of  ,
,
 .
Let
.
Let
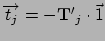 as before.
Generator matrix
as before.
Generator matrix
 is then defined by
is then defined by
where
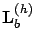 ,
,
 , and
, and
 are submatrices of
are submatrices of  as defined in Section 3.5.2,
as defined in Section 3.5.2,
Observe that the number of PH distributions used to approximate the
sojourn time distributions in levels 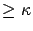 is reduced from
is reduced from  ,
in
,
in 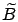 , to
, to 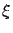 , in
, in  . The next approximation, DR-CI, uses only one PH
distribution.
. The next approximation, DR-CI, uses only one PH
distribution.




Next: Dimensionality reduction with complete
Up: Approximations of dimensionality reduction
Previous: Approximations of dimensionality reduction
Contents
Takayuki Osogami
2005-07-19
![]() has on how
the Markov chain enters levels
has on how
the Markov chain enters levels ![]() (from level
(from level ![]() ).
Specifically, we assume that
).
Specifically, we assume that ![]() is independent of
is independent of
![]() . Let
. Let
![]() for all
for all ![]() for each
for each ![]() , and let
, and let
![]() denote the process that is the same as
denote the process that is the same as ![]() except that
except that ![]() is replaced by
is replaced by ![]() for all
for all ![]() for each
for each ![]() .
Figure 3.27(a) shows the Markov chain for
the high priority jobs (background process) that we obtain via DR-PI in the analysis of an
M/PH/2 queue with two priority classes.
(Recall the Markov chain that we obtain via DR, Figure 3.5 in
Section 3.1, where
the four types of busy periods are
approximated by four PH distributions, respectively.)
In DR-PI, the four types of busy
periods are represented by two PH distributions, ignoring the
dependency that the duration of the busy period has on the phase of
the job in service at the beginning of the busy period.
.
Figure 3.27(a) shows the Markov chain for
the high priority jobs (background process) that we obtain via DR-PI in the analysis of an
M/PH/2 queue with two priority classes.
(Recall the Markov chain that we obtain via DR, Figure 3.5 in
Section 3.1, where
the four types of busy periods are
approximated by four PH distributions, respectively.)
In DR-PI, the four types of busy
periods are represented by two PH distributions, ignoring the
dependency that the duration of the busy period has on the phase of
the job in service at the beginning of the busy period.
![]() has the following
two key properties:
has the following
two key properties:
![]() ,
,
![]() , is determined as follows.
Let
, is determined as follows.
Let
![]() be the
be the ![]() -th moment of
-th moment of ![]() for
for
![]() for each
for each ![]() .
We determine
.
We determine
![]() so that
so that ![]() and
and ![]() have
the same marginal
have
the same marginal ![]() -th moment of the sojourn time in levels
-th moment of the sojourn time in levels ![]() :
:


