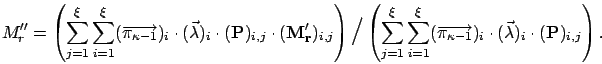DR-CI (DR with complete independence assumption) ignores not only the
dependency that the length of the sojourn time in levels ![]() has on how the Markov chain enters levels
has on how the Markov chain enters levels ![]() but also the dependency on
how it exits from levels
but also the dependency on
how it exits from levels ![]() (to level
(to level ![]() ).
Specifically, we assume that
).
Specifically, we assume that ![]() is independent of
is independent of ![]() and
and ![]() .
Let
.
Let ![]() for all
for all ![]() and
and ![]() , and let
, and let
![]() denote the process that is the same as
denote the process that is the same as ![]() except that
except that
![]() is replaced by
is replaced by ![]() for all
for all ![]() and
and ![]() .
Figure 3.27(b) shows the Markov chain for the high priority
jobs (background process) that is obtained via DR-CI in the analysis
of an M/PH/2 queue with two priority classes. In DR-CI, the four
types of busy periods are represented by a single PH
distribution, ignoring the dependency that the duration of the busy
period has on the phase of the job in service at the beginning and end
of the busy period.
.
Figure 3.27(b) shows the Markov chain for the high priority
jobs (background process) that is obtained via DR-CI in the analysis
of an M/PH/2 queue with two priority classes. In DR-CI, the four
types of busy periods are represented by a single PH
distribution, ignoring the dependency that the duration of the busy
period has on the phase of the job in service at the beginning and end
of the busy period.
We choose ![]() such that
such that
![]() has the above two key properties
that
has the above two key properties
that ![]() has. The difference between
has. The difference between ![]() and
and
![]() lies in the dependencies in the sequence of the
sojourn times in levels
lies in the dependencies in the sequence of the
sojourn times in levels ![]() . Observe that the sequence of the
sojourn times in levels
. Observe that the sequence of the
sojourn times in levels ![]() is i.i.d. in
is i.i.d. in
![]() ,
while it has some dependencies in
,
while it has some dependencies in ![]() .
.
More formally, the generator matrix
of
![]() ,
,
![]() , is determined as follows.
Let
, is determined as follows.
Let ![]() be the
be the ![]() -th moment of
-th moment of ![]() for
for ![]() .
We determine
.
We determine ![]() so that
so that
![]() and
and ![]() have
the same marginal
have
the same marginal ![]() -th moment of the sojourn time in levels
-th moment of the sojourn time in levels ![]() :
: