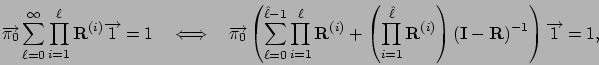We first discuss some key properties of the stationary probabilities
in a QBD process. Consider a simpler case of the birth-and-death
process having the generator matrix shown in (3.1).
Let ![]() be the stationary probability that the birth-and-death
process is in level
be the stationary probability that the birth-and-death
process is in level ![]() for
for ![]() . Then, it is easy to see
that
. Then, it is easy to see
that
![]() , where
, where
![]() , for
, for ![]() . It turns out that
the stationary probabilities in a QBD process have a similar property.
Let
. It turns out that
the stationary probabilities in a QBD process have a similar property.
Let
![]() be the stationary probability vector in a QBD
process having generator matrix shown in (3.2).
Here, the
be the stationary probability vector in a QBD
process having generator matrix shown in (3.2).
Here, the ![]() -th element of vector
-th element of vector
![]() denotes the
stationary probability that the QBD process is in phase
denotes the
stationary probability that the QBD process is in phase ![]() of level
of level
![]() , i.e. state (
, i.e. state (![]() ). It turns out that there exists a matrix
). It turns out that there exists a matrix
![]() such that
such that
![]() for each
for each ![]() .
.
Specifically, the stationary probability vector in the QBD process is
given recursively by
When the QBD process repeats after a certain level, ![]() , (i.e.,
, (i.e.,
![]() ,
,
![]() , and
, and
![]() for all
for all
![]() ),
),
![]() is the same for all
is the same for all ![]() , and
, and
![]() (for
(for ![]() ) is given by the
minimal nonnegative solution to the following matrix quadratic
equation3.3:
) is given by the
minimal nonnegative solution to the following matrix quadratic
equation3.3:
|
Once ![]() and
and
![]() 's are obtained,
the stationary probability vector
's are obtained,
the stationary probability vector
![]() can be calculated recursively from
can be calculated recursively from ![]() via (3.3) for
via (3.3) for ![]() . Thus, all that remains is to calculate
. Thus, all that remains is to calculate ![]() .
Vector
.
Vector ![]() is given by a positive solution of
is given by a positive solution of