



Next: Definition of MAP
Up: Markovian arrival process
Previous: Markovian arrival process
Contents
We start by providing canonical examples of MAPs. Again,
we provide both pictorial explanation and more formal explanation.
We will view a MAP as a
point process, which is a random sequence of ``events'' such as the
epochs of job arrivals.
Figure 3.9:
Examples of Markovian arrival processes.
|
(b) PH (Erlang-2) renewal
|
|
First, a Poisson process is a MAP. In a Poisson process, the intervals
between consecutive events are independent and identically distributed
exponential random variables.
Figure 3.9(a) illustrates
a Poisson process as the epochs of transitions in a Markov chain.
When there is a transition (from a state to itself) in the Markov
chain, there is an event in the Poisson process.
Recall the birth-and-death process modeling an M/M/1 queue
(Figure 3.8(a)),
where jobs arrive according to a Poisson process with rate 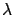 .
At the moment of an ``event'' in the Poisson process,
the number of jobs (or the level of the birth-and-death process) is
incremented by one.
.
At the moment of an ``event'' in the Poisson process,
the number of jobs (or the level of the birth-and-death process) is
incremented by one.
Second, a PH renewal process is a MAP. In a PH renewal process, the
intervals between consecutive events are independent and identically distributed
with a PH distribution.
Figure 3.9(b) illustrates a PH
renewal process, when the PH distribution is an Erlang-2 distribution,
as the epochs of some transitions in a Markov chain. There is a
transition (thick arrow) associated with an event. This transition corresponds the transition
into the absorbing state in the Markov chain whose absorption time defines the
Erlang-2 distribution (see Figure 2.6(b)). Thus, a PH renewal
process has an event when the Markov chain (for the PH distribution) transitions into the
absorbing state, and at this moment the Markov chain immediately transitions
back to a initial state according to the initial probability vector.
Figure 3.10(a) shows a QBD process modeling an Er/M/1 queue,
where jobs arrive according to a PH renewal process shown in Figure 3.9(b),
and their service demand has an exponential distribution with rate  .
.
Figure 3.10:
QBD processes for MAP/M/1 queues.
|
|
More formally, consider the PH(
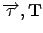 ) distribution (as defined in Section 2.2).
Let
) distribution (as defined in Section 2.2).
Let
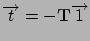 .
Matrix
.
Matrix
 ,
defines the generator matrix of a Markov chain.
For example, the above Erlang-2 distribution has parameters
,
defines the generator matrix of a Markov chain.
For example, the above Erlang-2 distribution has parameters

and hence

The nonzero  element of
element of
 is a transition associated with an event.
This transition can be seen as a transition into the absorbing state followed by
an instantaneous transition into a initial state following the initial probability vector
is a transition associated with an event.
This transition can be seen as a transition into the absorbing state followed by
an instantaneous transition into a initial state following the initial probability vector  .
The
.
The  element of
element of  is a transition that is not associated with an event
for
is a transition that is not associated with an event
for  .
.
Our third example, a Markov modulated Poisson process (MMPP), allows
correlation between inter-event times.
Figure 3.9(c) illustrates an MMPP of order
2, MMPP(2), as the epochs of some transitions in a Markov chain. There are
transitions (thick arrows) associated with events. The transitions
between the two states are not associated with events.
While the Markov chain is in state 1, events occur with rate  ,
and while the Markov chain is in state 2, events occur with rate
,
and while the Markov chain is in state 2, events occur with rate 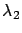 .
For example, an MMPP(2) can be seen as a job arrival process which alternates
between high arrival period (state 1) and low arrival period (state 2).
During the high arrival period, the arrival rate is
.
For example, an MMPP(2) can be seen as a job arrival process which alternates
between high arrival period (state 1) and low arrival period (state 2).
During the high arrival period, the arrival rate is  ,
and during the low arrival period, the arrival rate is
,
and during the low arrival period, the arrival rate is 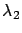 , where
, where
 .
Figure 3.10(b) shows a QBD process modeling an MMPP(2)/M/1 queue,
where jobs arrive according to a MMPP(2) process shown in Figure 3.9(c),
and their service demand has an exponential distribution with rate
.
Figure 3.10(b) shows a QBD process modeling an MMPP(2)/M/1 queue,
where jobs arrive according to a MMPP(2) process shown in Figure 3.9(c),
and their service demand has an exponential distribution with rate  .
.
More formally, the Markov chain in Figure 3.9(c) has
infinitesimal generator
where
The nonzero  element of
element of  is a transition associated with an event in the MMPP(2), and
the
is a transition associated with an event in the MMPP(2), and
the  element of
element of  (here,
(here,  ) is a transition that is not associated with an event.
) is a transition that is not associated with an event.




Next: Definition of MAP
Up: Markovian arrival process
Previous: Markovian arrival process
Contents
Takayuki Osogami
2005-07-19
![]() .
At the moment of an ``event'' in the Poisson process,
the number of jobs (or the level of the birth-and-death process) is
incremented by one.
.
At the moment of an ``event'' in the Poisson process,
the number of jobs (or the level of the birth-and-death process) is
incremented by one.
![]() .
.
![]() ) distribution (as defined in Section 2.2).
Let
) distribution (as defined in Section 2.2).
Let
![]() .
Matrix
.
Matrix
![]() ,
defines the generator matrix of a Markov chain.
For example, the above Erlang-2 distribution has parameters
,
defines the generator matrix of a Markov chain.
For example, the above Erlang-2 distribution has parameters


![]() ,
and while the Markov chain is in state 2, events occur with rate
,
and while the Markov chain is in state 2, events occur with rate ![]() .
For example, an MMPP(2) can be seen as a job arrival process which alternates
between high arrival period (state 1) and low arrival period (state 2).
During the high arrival period, the arrival rate is
.
For example, an MMPP(2) can be seen as a job arrival process which alternates
between high arrival period (state 1) and low arrival period (state 2).
During the high arrival period, the arrival rate is ![]() ,
and during the low arrival period, the arrival rate is
,
and during the low arrival period, the arrival rate is ![]() , where
, where
![]() .
Figure 3.10(b) shows a QBD process modeling an MMPP(2)/M/1 queue,
where jobs arrive according to a MMPP(2) process shown in Figure 3.9(c),
and their service demand has an exponential distribution with rate
.
Figure 3.10(b) shows a QBD process modeling an MMPP(2)/M/1 queue,
where jobs arrive according to a MMPP(2) process shown in Figure 3.9(c),
and their service demand has an exponential distribution with rate ![]() .
.
