



Next: QBD process modeling MAP/PH/1/FCFS
Up: Markovian arrival process
Previous: Examples of Markovian arrival
Contents
In general, a MAP is a point process defined by the epochs of
some transitions in a Markov chain.
Definition 15
Consider a Markov chain with infinitesimal generator
 , where all the off-diagonal
elements of
, where all the off-diagonal
elements of  and all the elements of
and all the elements of  are
nonnegative. The transitions associated with
are
nonnegative. The transitions associated with  are
called type 1 transitions. A MAP with parameters
(
are
called type 1 transitions. A MAP with parameters
(
 ), MAP(
), MAP(
 ), is a
point process where an event occurs when a type 1 transition occurs in
the Markov chain.
), is a
point process where an event occurs when a type 1 transition occurs in
the Markov chain.
Figure 3.11 illustrates a MAP of order 2
having parameters
where
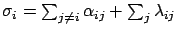 for
for  ..
..
Figure 3.11:
A MAP(2). Transitions shown in thick arrows (transitions with  )
are associated with events in the MAP(2). Transitions with
)
are associated with events in the MAP(2). Transitions with  only change the state.
only change the state.
|
|
To completely specify a MAP, the initial probability vector in the
Markov chain needs to be specified. Throughout, we assume that the
initial probability vector is the same as the stationary probability
vector. That is, our MAPs are stationary MAPs.
A MAP(
 ) is called a Markov modulated
Poisson process, MMPP, if
) is called a Markov modulated
Poisson process, MMPP, if  is diagonal. That is,
in the Markov chain that defines an MMPP, all the transitions that are
associated with events do not change the state.
is diagonal. That is,
in the Markov chain that defines an MMPP, all the transitions that are
associated with events do not change the state.




Next: QBD process modeling MAP/PH/1/FCFS
Up: Markovian arrival process
Previous: Examples of Markovian arrival
Contents
Takayuki Osogami
2005-07-19

![\includegraphics[width=.23\linewidth]{fig/MAP2.eps}](img571.png)
![]() ) is called a Markov modulated
Poisson process, MMPP, if
) is called a Markov modulated
Poisson process, MMPP, if ![]() is diagonal. That is,
in the Markov chain that defines an MMPP, all the transitions that are
associated with events do not change the state.
is diagonal. That is,
in the Markov chain that defines an MMPP, all the transitions that are
associated with events do not change the state.