QBD process modeling MAP/PH/1/FCFS queue

The QBD process that models a MAP/PH/1 queue length has a compact and convenient representation when we use the notation introduced above and in Section 2.2,

Consider a simpler case of an M/PH/1 queue, where jobs arrive according to a Poisson process with rate $\lambda$, and the service demand has a PH( $\Vec\tau,\mathbf{T}$) distribution. The generator matrix for the queue length can be represented as

$$\mathbf{\widehat Q} = \left(\begin{array}{lllll} \mathbf{\wi... ...hat F} & \\ & & \ddots & \ddots & \ddots \end{array}\right),$$

where $\mathbf{\widehat F} = \lambda \mathbf{\widehat I}$, $\mathbf{\widehat B} = \Vec{t}\Vec\tau$, $\mathbf{\widehat L} = \mathbf{T} - \lambda \mathbf{\widehat I}$, and $\mathbf{\widehat L}^{(0)}=-\lambda\mathbf{\widehat I}$. Here, $\mathbf{\widehat I}$ is an identity matrix of order equal to $\mathbf{T}$, and $\Vec{t}=-\mathbf{T}\Vec{1}$.

Next, consider a MAP/M/1 queue, where jobs arrive according to a MAP($\mathbf{D}_0$,$\mathbf{D}_1$), and the service demand has an exponential distribution with rate $\mu$. The generator matrix for the queue length can be represented as

$$\mathbf{\check Q} = \left(\begin{array}{lllll} \mathbf{\chec... ...eck F} & \\ & & \ddots & \ddots & \ddots \end{array}\right),$$

where $\mathbf{\check F} = \mathbf{D}_1$, $\mathbf{\check B} = \mu \mathbf{\check I}$, $\mathbf{\check L} = \mathbf{D}_0 - \mu \mathbf{\check I}$, and $\mathbf{\check L}^{(0)}=\mathbf{D}_0$. Here, $\mathbf{\check I}$ is an identity matrix of order equal to $\mathbf{D}_0$.

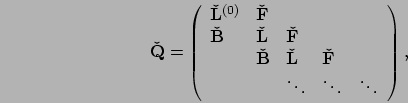
Finally, consider a MAP/PH/1 queue, where jobs arrive according to a MAP($\mathbf{D}_0$,$\mathbf{D}_1$), and the service demand has a PH( $\tau,\mathbf{T}$) distribution. The generator matrix for the queue length can be represented as

$$\mathbf{Q} = \left(\begin{array}{lllll} \mathbf{L}^{(0)}& \m... ...thbf{F} & \\ & & \ddots & \ddots & \ddots \end{array}\right)$$

where $\mathbf{F} = \mathbf{D}_1 \otimes \mathbf{\widehat I}$, $\mathbf{B} = \mathbf{\check I} \otimes \Vec{t}\Vec\tau$, $\mathbf{L} = \mathbf{\check I} \otimes \mathbf{T} + \mathbf{D}_0 \otimes \mathbf{\widehat I}$, and $\mathbf{L}^{(0)} = \mathbf{D}_0 \otimes \mathbf{\widehat I}$, where $\otimes$ denotes the Kronecker product. Observe that the QBD process for a MAP/PH/1 queue can be expressed as a ``superposition'' of the QBD processes for an M/PH/1 queue and a MAP/M/1 queue: specifically, $\mathbf{F} = \mathbf{\check F} \otimes \mathbf{\widehat I}$, $\mathbf{B} = \mathbf{\check I} \otimes \mathbf{\widehat B}$, $\mathbf{L} = \mathbf{\check I} \otimes (\mathbf{\widehat L}-\mathbf{\widehat L}^{(0)}) + \mathbf{\check L}^{(0)} \otimes \mathbf{\widehat I}$, and $\mathbf{L}^{(0)} = \mathbf{\check L}^{(0)} \otimes \mathbf{\widehat I}$.