



Next: Equal mean sizes
Up: Configuring multiserver systems with
Previous: How many servers are
Contents
How many servers are best in priority system?
In this section, we study the question of ``how many servers are
best?'' in an M/PH/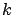 queue with two priority classes with respect to
minimizing mean response time. The M/PH/
queue with two priority classes with respect to
minimizing mean response time. The M/PH/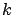 queue with two priority
classes can be modeled as a foreground-background (FB) process, as discussed in
Section 3.4, and the analysis of the FB process via DR
(see Chapter 3) provides mean response time of high
priority jobs and low priority jobs, respectively.
queue with two priority
classes can be modeled as a foreground-background (FB) process, as discussed in
Section 3.4, and the analysis of the FB process via DR
(see Chapter 3) provides mean response time of high
priority jobs and low priority jobs, respectively.
Throughout our evaluations, we will consider a range of load typically
shown on the horizontal axis, and a range of variability in the high
priority job sizes, typically shown on the vertical axis. When we
vary the load, we vary only the arrival rates and keep the job size
distributions. In all the results shown, the size of the high
priority jobs has a two phase Coxian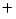 PH distribution (as defined
in Section 2.2). The mean job size for the high
priority jobs is held fixed at
PH distribution (as defined
in Section 2.2). The mean job size for the high
priority jobs is held fixed at
![$\mbox{{\bf\sf E}}\left[ X_H \right]=1$](img1206.png) , and its squared
coefficient of variation is varied (
, and its squared
coefficient of variation is varied (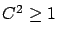 )4.2.
On the other hand, throughout, we assume that the size of the low
priority job has an exponential distribution (
)4.2.
On the other hand, throughout, we assume that the size of the low
priority job has an exponential distribution (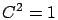 ), since the
effect of its variability is less interesting to study, as it affects
only the performance of low priority jobs. We consider three
different mean sizes,
), since the
effect of its variability is less interesting to study, as it affects
only the performance of low priority jobs. We consider three
different mean sizes,
![$\mbox{{\bf\sf E}}\left[ X_L \right]$](img1208.png) , for the low priority jobs: (i)
, for the low priority jobs: (i)
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1209.png) , (ii)
, (ii)
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 10$](img1210.png) , and (iii)
, and (iii)
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1/10$](img1211.png) . Note
that the mean service time changes depending on how many servers are
in the system (1 fast server or
. Note
that the mean service time changes depending on how many servers are
in the system (1 fast server or 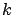 slow servers) so that the systems
are comparable. The values specified above for
slow servers) so that the systems
are comparable. The values specified above for
![$\mbox{{\bf\sf E}}\left[ X_H \right]$](img1212.png) and
and
![$\mbox{{\bf\sf E}}\left[ X_L \right]$](img1208.png) are the values for the maximum number of servers used in each plot and
the mean sizes for each of the other number of servers is scaled
appropriately. Finally, note that when we compare a dual priority
system with its single priority counterpart (high priority jobs and
low priority jobs are aggregated into a single class and served in
FCFS order), the job size of the single aggregate class has a PH
distribution that is a mixture of the two-phase PH distribution (for
the high priority job size) and the exponential distribution (for the
low priority job size).
are the values for the maximum number of servers used in each plot and
the mean sizes for each of the other number of servers is scaled
appropriately. Finally, note that when we compare a dual priority
system with its single priority counterpart (high priority jobs and
low priority jobs are aggregated into a single class and served in
FCFS order), the job size of the single aggregate class has a PH
distribution that is a mixture of the two-phase PH distribution (for
the high priority job size) and the exponential distribution (for the
low priority job size).
Figure 4.2:
How many servers are best when the two priority classes have the same mean job size?
(i)
![$\mbox{{\bf\sf E}}\left[ X_H \right]=1$](img1213.png) and and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1214.png)
(a)
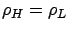 |
(b)
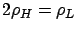 |
|
Figures 4.2-4.4 illustrate the results of our analysis
for the three cases: (i)
![$\mbox{{\bf\sf E}}\left[ X_H \right]=1$](img1206.png) and
and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1$](img1209.png) , (ii)
, (ii)
![$\mbox{{\bf\sf E}}\left[ X_H \right]=1$](img1206.png) and
and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 10$](img1210.png) , and (iii)
, and (iii)
![$\mbox{{\bf\sf E}}\left[ X_H \right]=1$](img1206.png) and
and
![$\mbox{{\bf\sf E}}\left[ X_L \right] = 1/10$](img1211.png) , respectively. For each figure, column (a) shows the case
where the load made up by high and low priority jobs is equal (
, respectively. For each figure, column (a) shows the case
where the load made up by high and low priority jobs is equal (
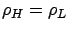 ), and
column (b) shows the case where
), and
column (b) shows the case where
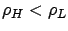 . We also
discuss, but omit showing, the case where
. We also
discuss, but omit showing, the case where
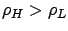 .
For each figure we consider both the case of dual priority classes
and the case of a single aggregate class.
.
For each figure we consider both the case of dual priority classes
and the case of a single aggregate class.
Subsections




Next: Equal mean sizes
Up: Configuring multiserver systems with
Previous: How many servers are
Contents
Takayuki Osogami
2005-07-19
![]() PH distribution (as defined
in Section 2.2). The mean job size for the high
priority jobs is held fixed at
PH distribution (as defined
in Section 2.2). The mean job size for the high
priority jobs is held fixed at
![]() , and its squared
coefficient of variation is varied (
, and its squared
coefficient of variation is varied (![]() )4.2.
On the other hand, throughout, we assume that the size of the low
priority job has an exponential distribution (
)4.2.
On the other hand, throughout, we assume that the size of the low
priority job has an exponential distribution (![]() ), since the
effect of its variability is less interesting to study, as it affects
only the performance of low priority jobs. We consider three
different mean sizes,
), since the
effect of its variability is less interesting to study, as it affects
only the performance of low priority jobs. We consider three
different mean sizes,
![]() , for the low priority jobs: (i)
, for the low priority jobs: (i)
![]() , (ii)
, (ii)
![]() , and (iii)
, and (iii)
![]() . Note
that the mean service time changes depending on how many servers are
in the system (1 fast server or
. Note
that the mean service time changes depending on how many servers are
in the system (1 fast server or ![]() slow servers) so that the systems
are comparable. The values specified above for
slow servers) so that the systems
are comparable. The values specified above for
![]() and
and
![]() are the values for the maximum number of servers used in each plot and
the mean sizes for each of the other number of servers is scaled
appropriately. Finally, note that when we compare a dual priority
system with its single priority counterpart (high priority jobs and
low priority jobs are aggregated into a single class and served in
FCFS order), the job size of the single aggregate class has a PH
distribution that is a mixture of the two-phase PH distribution (for
the high priority job size) and the exponential distribution (for the
low priority job size).
are the values for the maximum number of servers used in each plot and
the mean sizes for each of the other number of servers is scaled
appropriately. Finally, note that when we compare a dual priority
system with its single priority counterpart (high priority jobs and
low priority jobs are aggregated into a single class and served in
FCFS order), the job size of the single aggregate class has a PH
distribution that is a mixture of the two-phase PH distribution (for
the high priority job size) and the exponential distribution (for the
low priority job size).
![]() and
and
![]() , (ii)
, (ii)
![]() and
and
![]() , and (iii)
, and (iii)
![]() and
and
![]() , respectively. For each figure, column (a) shows the case
where the load made up by high and low priority jobs is equal (
, respectively. For each figure, column (a) shows the case
where the load made up by high and low priority jobs is equal (
![]() ), and
column (b) shows the case where
), and
column (b) shows the case where
![]() . We also
discuss, but omit showing, the case where
. We also
discuss, but omit showing, the case where
![]() .
For each figure we consider both the case of dual priority classes
and the case of a single aggregate class.
.
For each figure we consider both the case of dual priority classes
and the case of a single aggregate class.