



Next: Distribution and moments of
Up: Dimensionality reduction of Markov
Previous: Generalization
Contents
Computing various performance measures
So far, our focus has been on computing the stationary probabilities
in the RFB/GFB process. In this section, we discuss how the
stationary probabilities can be used to compute other performance
measures. In Section 3.8.1, we consider the distribution of
the number of jobs in the system and its moments. In
Section 3.8.2, we consider the distribution of response time
and its moments. Since the computation of these performance measures
depends on particular multiserver systems and details of modeling, we
will illustrate the approach via an example in the case of an M/M/2 queue
with two preemptive priority classes (recall Figure 3.3),
and briefly discuss how this can be applied to other multiserver systems.
Figure 3.28:
Markov chains whose stationary probabilities are computed via DR
in the analysis of an M/M/2 queue with two preemptive priority classes.
|
|
Figure 3.28 shows the Markov chains whose stationary
probabilities are computed via DR in the analysis of an M/M/2 queue
with two preemptive priority classes. Figure 3.28(a) shows
the background process, where state (level) 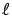 corresponds to the
state with
corresponds to the
state with 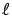 high priority jobs for
high priority jobs for 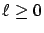 .
Let
.
Let
 be the stationary probability in
state (level)
be the stationary probability in
state (level) 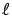 of the background process.
Observe that
of the background process.
Observe that
 is the probability that there are
is the probability that there are 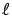 high priority jobs in the system for
high priority jobs in the system for 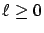 .
Figure 3.28(b) shows the 1D Markov chain reduced from the
2D Markov chain (FB process), where level
.
Figure 3.28(b) shows the 1D Markov chain reduced from the
2D Markov chain (FB process), where level 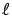 consists of the states
with
consists of the states
with 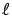 low priority jobs for
low priority jobs for 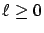 .
Let
.
Let
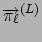 be the stationary probability vector in
level
be the stationary probability vector in
level 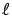 of the 1D Markov chain shown in Figure 3.28(b).
Observe that
of the 1D Markov chain shown in Figure 3.28(b).
Observe that
 is the probability that
there are
is the probability that
there are 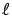 low priority jobs in the system for
low priority jobs in the system for 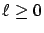 .
.
Subsections




Next: Distribution and moments of
Up: Dimensionality reduction of Markov
Previous: Generalization
Contents
Takayuki Osogami
2005-07-19
![]() corresponds to the
state with
corresponds to the
state with ![]() high priority jobs for
high priority jobs for ![]() .
Let
.
Let
![]() be the stationary probability in
state (level)
be the stationary probability in
state (level) ![]() of the background process.
Observe that
of the background process.
Observe that
![]() is the probability that there are
is the probability that there are ![]() high priority jobs in the system for
high priority jobs in the system for ![]() .
Figure 3.28(b) shows the 1D Markov chain reduced from the
2D Markov chain (FB process), where level
.
Figure 3.28(b) shows the 1D Markov chain reduced from the
2D Markov chain (FB process), where level ![]() consists of the states
with
consists of the states
with ![]() low priority jobs for
low priority jobs for ![]() .
Let
.
Let
![]() be the stationary probability vector in
level
be the stationary probability vector in
level ![]() of the 1D Markov chain shown in Figure 3.28(b).
Observe that
of the 1D Markov chain shown in Figure 3.28(b).
Observe that
![]() is the probability that
there are
is the probability that
there are ![]() low priority jobs in the system for
low priority jobs in the system for ![]() .
.