



Next: Effect of donor job
Up: Mean response time
Previous: Benefits of cycle stealing:
Contents
Benefit of cycle stealing:

For
 ,
cycle stealing has regions of high gain and low pain and also regions
where the reverse is true. These regions depend on job sizes,
switching times, and loads.
,
cycle stealing has regions of high gain and low pain and also regions
where the reverse is true. These regions depend on job sizes,
switching times, and loads.
In Figure 6.5, we categorize
performance into these gain/pain regions and also look at the overall mean response time (averaged over both beneficiary and donor
jobs) to determine whether cycle stealing is ``good'' or ``bad''
overall. In general under higher 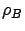 and lower
and lower 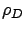 , cycle
stealing is ``good'' overall, because the gain of the beneficiary jobs is
so high in this region. We will find that when the switching times
are short, cycle stealing leads to high gain and low pain. However long
switching times can reverse this effect. More important than the
absolute switching times are the switching times relative to the mean
donor job size. We will find that the mean response time of the
donor jobs is sensitive to the switching times, while surprisingly the
mean response time of the beneficiary jobs is far less sensitive.
, cycle
stealing is ``good'' overall, because the gain of the beneficiary jobs is
so high in this region. We will find that when the switching times
are short, cycle stealing leads to high gain and low pain. However long
switching times can reverse this effect. More important than the
absolute switching times are the switching times relative to the mean
donor job size. We will find that the mean response time of the
donor jobs is sensitive to the switching times, while surprisingly the
mean response time of the beneficiary jobs is far less sensitive.
Figure 6.5:
The gain of beneficiary jobs and pain of donor jobs ((a) and (c))
and the effect of cycle stealing on the overall mean response time relative to
dedicated servers ((b) and (d)).
In (a) and (c), solid lines delineate high/mid/low gain regions, and
dashed lines delineate high/mid/low pain regions.
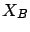 and
and  have exponential distributions, and their
means are as labeled.
Switching times are exponential with mean 0 or
1 as labeled, where
have exponential distributions, and their
means are as labeled.
Switching times are exponential with mean 0 or
1 as labeled, where
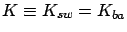 .
.
Gain of beneficiary jobs & pain of donor jobs (
![$\mbox{{\bf\sf E}}\left[ X_B \right]=1,\mbox{{\bf\sf E}}\left[ X_D \right]=1$](img1472.png) ) )
Gain of beneficiary jobs & pain of donor jobs (
![$\mbox{{\bf\sf E}}\left[ X_B \right]=1,\mbox{{\bf\sf E}}\left[ X_D \right]=10$](img1477.png) ) )
Gain of beneficiary jobs & pain of donor jobs (
![$\mbox{{\bf\sf E}}\left[ X_B \right]=10,\mbox{{\bf\sf E}}\left[ X_D \right]=1$](img1482.png) ) )
(a)
![$\mbox{{\bf\sf E}}\left[ K \right]=0$](img1459.png) |
(b)
![$\mbox{{\bf\sf E}}\left[ K \right]=0$](img1459.png) |
(c)
![$\mbox{{\bf\sf E}}\left[ K \right]=1$](img1461.png) |
(d)
![$\mbox{{\bf\sf E}}\left[ K \right]=1$](img1461.png) |
|
Figure 6.5 shows the gain of beneficiary jobs and the
pain of donor jobs, where  . The odd-numbered columns of
Figure 6.5 divide the (
. The odd-numbered columns of
Figure 6.5 divide the (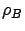 ,
,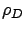 ) space into
regions of beneficiary gain and donor pain (low, mid, and high). We
define low gain as a gain of
) space into
regions of beneficiary gain and donor pain (low, mid, and high). We
define low gain as a gain of  or less; mid gain as a
gain of between
or less; mid gain as a
gain of between  and
and  ; and high gain as a gain of over
; and high gain as a gain of over
 . Pain regions are defined similarly. While odd-numbered
columns of Figure 6.5 consider the beneficiary and
donor mean response time individually, the even-numbered columns of
Figure 6.5 look at the overall mean response time and
ask whether cycle stealing is ``good'' or ``bad'' with respect to the
overall mean response time. The effect of mean job sizes is
considered in Figure 6.5, where
job sizes are exponential with mean 1 or 10.
. Pain regions are defined similarly. While odd-numbered
columns of Figure 6.5 consider the beneficiary and
donor mean response time individually, the even-numbered columns of
Figure 6.5 look at the overall mean response time and
ask whether cycle stealing is ``good'' or ``bad'' with respect to the
overall mean response time. The effect of mean job sizes is
considered in Figure 6.5, where
job sizes are exponential with mean 1 or 10.
Consider first row 1 in Figure 6.5. Under zero
switching time (a)-(b), all regions are low pain regions (in fact zero pain),
and higher 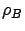 yields higher gain for the beneficiary jobs.
Non-zero switching times (c)-(d) create
only slightly reduced gain for the beneficiary jobs, but they
create pain for the donor jobs. When
yields higher gain for the beneficiary jobs.
Non-zero switching times (c)-(d) create
only slightly reduced gain for the beneficiary jobs, but they
create pain for the donor jobs. When 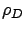 is very low, the pain
appears high, but this is primarily due to the fact that ``pain'' is
relative to the mean response time under dedicated servers, which is
clearly low for small
is very low, the pain
appears high, but this is primarily due to the fact that ``pain'' is
relative to the mean response time under dedicated servers, which is
clearly low for small 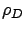 .
Although not shown, we have also
investigated longer switching times, and these lead to the same trend
of slightly less gain for beneficiary jobs and significantly more pain
for donor jobs.
.
Although not shown, we have also
investigated longer switching times, and these lead to the same trend
of slightly less gain for beneficiary jobs and significantly more pain
for donor jobs.
We now consider the effect of changes in job sizes. Row 2 of
Figure 6.5 differs from row 1 only in  , which now
has mean 10. The effect of this change is dramatic: now a switching
time of 1 has almost no effect on either beneficiary jobs or donor jobs.
This makes sense since the setup time experienced by donor jobs is now
relatively small compared to their size. Row 3 in
Figure 6.5 differs from row 1 only in
, which now
has mean 10. The effect of this change is dramatic: now a switching
time of 1 has almost no effect on either beneficiary jobs or donor jobs.
This makes sense since the setup time experienced by donor jobs is now
relatively small compared to their size. Row 3 in
Figure 6.5 differs from row 1 only in 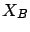 , which now
has mean 10. Comparing these rows, we see the increase in
, which now
has mean 10. Comparing these rows, we see the increase in
![$\mbox{{\bf\sf E}}\left[ X_B \right]$](img1489.png) has a surprisingly small effect on both beneficiary jobs and donor jobs, as
compared with increasing
has a surprisingly small effect on both beneficiary jobs and donor jobs, as
compared with increasing
![$\mbox{{\bf\sf E}}\left[ X_D \right]$](img1383.png) . This is because the donor still
experiences the setup time, which has the same mean size as the donor
job. We can conclude that cycle stealing is most effective when the switching time
is small relative to the size of the donor jobs.
. This is because the donor still
experiences the setup time, which has the same mean size as the donor
job. We can conclude that cycle stealing is most effective when the switching time
is small relative to the size of the donor jobs.
Focusing on columns 2 and 4 of Figure 6.5, which
depict the effect on overall mean response time, we see that, for all rows,
when the switching time is zero, cycle stealing always overwhelms
the dedicated policy. When switching time is non-zero, cycle stealing
is a good idea provided either 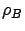 is high, or the switching time
is short compared to
is high, or the switching time
is short compared to  . These trends continue for
longer switching times.
. These trends continue for
longer switching times.




Next: Effect of donor job
Up: Mean response time
Previous: Benefits of cycle stealing:
Contents
Takayuki Osogami
2005-07-19
, cycle stealing has regions of high gain and low pain and also regions where the reverse is true. These regions depend on job sizes, switching times, and loads.
![]() and lower
and lower ![]() , cycle
stealing is ``good'' overall, because the gain of the beneficiary jobs is
so high in this region. We will find that when the switching times
are short, cycle stealing leads to high gain and low pain. However long
switching times can reverse this effect. More important than the
absolute switching times are the switching times relative to the mean
donor job size. We will find that the mean response time of the
donor jobs is sensitive to the switching times, while surprisingly the
mean response time of the beneficiary jobs is far less sensitive.
, cycle
stealing is ``good'' overall, because the gain of the beneficiary jobs is
so high in this region. We will find that when the switching times
are short, cycle stealing leads to high gain and low pain. However long
switching times can reverse this effect. More important than the
absolute switching times are the switching times relative to the mean
donor job size. We will find that the mean response time of the
donor jobs is sensitive to the switching times, while surprisingly the
mean response time of the beneficiary jobs is far less sensitive.
![]() . The odd-numbered columns of
Figure 6.5 divide the (
. The odd-numbered columns of
Figure 6.5 divide the (![]() ,
,![]() ) space into
regions of beneficiary gain and donor pain (low, mid, and high). We
define low gain as a gain of
) space into
regions of beneficiary gain and donor pain (low, mid, and high). We
define low gain as a gain of ![]() or less; mid gain as a
gain of between
or less; mid gain as a
gain of between ![]() and
and ![]() ; and high gain as a gain of over
; and high gain as a gain of over
![]() . Pain regions are defined similarly. While odd-numbered
columns of Figure 6.5 consider the beneficiary and
donor mean response time individually, the even-numbered columns of
Figure 6.5 look at the overall mean response time and
ask whether cycle stealing is ``good'' or ``bad'' with respect to the
overall mean response time. The effect of mean job sizes is
considered in Figure 6.5, where
job sizes are exponential with mean 1 or 10.
. Pain regions are defined similarly. While odd-numbered
columns of Figure 6.5 consider the beneficiary and
donor mean response time individually, the even-numbered columns of
Figure 6.5 look at the overall mean response time and
ask whether cycle stealing is ``good'' or ``bad'' with respect to the
overall mean response time. The effect of mean job sizes is
considered in Figure 6.5, where
job sizes are exponential with mean 1 or 10.
![]() yields higher gain for the beneficiary jobs.
Non-zero switching times (c)-(d) create
only slightly reduced gain for the beneficiary jobs, but they
create pain for the donor jobs. When
yields higher gain for the beneficiary jobs.
Non-zero switching times (c)-(d) create
only slightly reduced gain for the beneficiary jobs, but they
create pain for the donor jobs. When ![]() is very low, the pain
appears high, but this is primarily due to the fact that ``pain'' is
relative to the mean response time under dedicated servers, which is
clearly low for small
is very low, the pain
appears high, but this is primarily due to the fact that ``pain'' is
relative to the mean response time under dedicated servers, which is
clearly low for small ![]() .
Although not shown, we have also
investigated longer switching times, and these lead to the same trend
of slightly less gain for beneficiary jobs and significantly more pain
for donor jobs.
.
Although not shown, we have also
investigated longer switching times, and these lead to the same trend
of slightly less gain for beneficiary jobs and significantly more pain
for donor jobs.
![]() , which now
has mean 10. The effect of this change is dramatic: now a switching
time of 1 has almost no effect on either beneficiary jobs or donor jobs.
This makes sense since the setup time experienced by donor jobs is now
relatively small compared to their size. Row 3 in
Figure 6.5 differs from row 1 only in
, which now
has mean 10. The effect of this change is dramatic: now a switching
time of 1 has almost no effect on either beneficiary jobs or donor jobs.
This makes sense since the setup time experienced by donor jobs is now
relatively small compared to their size. Row 3 in
Figure 6.5 differs from row 1 only in ![]() , which now
has mean 10. Comparing these rows, we see the increase in
, which now
has mean 10. Comparing these rows, we see the increase in
![]() has a surprisingly small effect on both beneficiary jobs and donor jobs, as
compared with increasing
has a surprisingly small effect on both beneficiary jobs and donor jobs, as
compared with increasing
![]() . This is because the donor still
experiences the setup time, which has the same mean size as the donor
job. We can conclude that cycle stealing is most effective when the switching time
is small relative to the size of the donor jobs.
. This is because the donor still
experiences the setup time, which has the same mean size as the donor
job. We can conclude that cycle stealing is most effective when the switching time
is small relative to the size of the donor jobs.
![]() is high, or the switching time
is short compared to
is high, or the switching time
is short compared to ![]() . These trends continue for
longer switching times.
. These trends continue for
longer switching times.