Effect of donor job size variability

Figure 6.6: The gain of beneficiary jobs and pain of donor jobs ((a) and (c)), and the effect of cycle stealing on the overall mean response time relative to dedicated servers ((b) and (d)). In (a) and (c), solid lines delineate high/mid/low gain regions, and dashed lines delineate high/mid/low pain regions. $X_B$ has an exponential distribution; $X_D$ has a PH distribution with $C_D^2=8$. The means of $X_B$ and $X_D$ are as labeled. Switching times are exponential with mean 0 or 1 as labeled, where $K\equiv K_{sw}=K_{ba}$.

Gain of beneficiary jobs & pain of donor jobs ( $\mbox{{\bf\sf E}}\left[ X_B \right]=\mbox{{\bf\sf E}}\left[ X_D \right]=1,C_D^2=8$)

(a) $\mbox{{\bf\sf E}}\left[ K \right]=0$

(b) $\mbox{{\bf\sf E}}\left[ K \right]=0$

(c) $\mbox{{\bf\sf E}}\left[ K \right]=1$

(d) $\mbox{{\bf\sf E}}\left[ K \right]=1$

For $.5 < \rho_B < 1$, variability of donor job sizes has very little effect on beneficiary mean response time.

For $.5 < \rho_B < 1$, we find variability of donor job sizes has very little effect on beneficiary mean response time. This finding surprised us; we expected the beneficiary to gain far less from the bursty help of a donor with irregular (highly variable) job sizes.

It seems intuitive that when donor job sizes are made more variable, two things should happen. (i) The donor pain should drop. This is because the donor mean response times will be higher overall, and so the relative pain will appear diminished. (ii) The beneficiary gain should drop. This is because high variability in the donor job sizes implies high variability in the length of the donor busy periods, which implies that the donor's visits to the beneficiary queue will be more irregular. Sporadic help should be inferior to regular help for the beneficiary. Figure 6.6 shows that hypothesis (i) is in fact true, while hypothesis (ii) is surprisingly false, at least for $\rho_B < 1$. Comparing Figure 6.5 row 1 ($X_D$ has low variability: $C^2_D = 1$) with Figure 6.6 ($X_D$ has high variability: $C^2_D = 8$), we see that there is no discernible difference in beneficiary performance.

To study this effect more closely, we next increase the variability in donor job sizes further. Figure 6.7(a) shows the mean response time of the beneficiary jobs when $C_D^2$ is 1, 8, or 50. Figure 6.7(b) shows the ``impact'' of $C_D^2$ on the mean response time of the beneficiary jobs, where the ``impact'' is defined to be the mean response time of the beneficiary jobs when $C_D^2>1$ (specifically, two cases where $C_D^2=8,50$ are shown) relative to the mean response time of the beneficiary jobs when $C_D^2=1$. 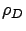In Figure 6.7, switching times are set zero, $\rho_D$ is fixed at 0.5, and 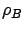$\rho _B$ is varied from 0 to $\rho_B^{\max}$. 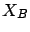As observed in Figure 6.6, the effect of the variability of $X_D$ on the mean response time of $X_B$ is small at $\rho_B < 1$, and negligible at $\rho_B<0.75$, when $C_D^2=8$, although this effect increases slightly when $C_D^2$. When $\rho_B>1$ the effect of variability in donor sizes can be significant. A critical factor seems to be whether the beneficiary queue is stable in isolation; when this is not the case, high variability in donor visits leads to prolonged intervals of instability, which inflates the mean response time.

This is the same phenomenon seen in other related models studied by Borst, Boxma and van Uitert [25] and by Borst, Boxma and Jelenkovic [26] as well as in Chapter 5. Borst, Boxma and van Uitert study the coupled processor model, where two processors each serve their own class of jobs, and if either is idle it may help the other, increasing the rate of the other processor. This help incurs no switching time and has a benefit even if only a single job is present (i.e. two processors can work on the single job). They find that if a processor has a load less than one, it is ``insulated'' from the heavy-tail of the other, as long periods without cooperation will not lead to large backlogs. This is not the case if the load is greater than one, as the queue now must rely on help to be stable. Borst, Boxma and Jelenkovic study the generalized processor sharing, where $n$ classes of jobs can share a processor with arbitrary weights. Using probabilistic bounds, they show that different service rates can either insulate the performance of different classes from the others or not, again depending on whether the non-cooperative load is larger than one.

Figure 6.7: (a) The mean response time of the beneficiary jobs under different donor job size variability; (b) the ``impact'' of donor job size variability on the mean response time of the beneficiary jobs (the vertical axis is shown in the log scale). We fix $\rho_D$ at 0.5, and $\rho _B$ varies from 0 to the stability condition of 1.5. Switching time is zero; $X_D$ and $X_B$ have mean 1.

Effect of donor job variability on beneficiary jobs

(a)

(b)