



Next: Static robustness and mean
Up: Static robustness and mean
Previous: Case 2:
Contents
Static robustness of single-threshold allocation policies
We next study static robustness of the T1 and T2 policies by
evaluating the mean response time of these policies under a range of
loads. In particular, we examine how a policy (T1 or T2) tuned for
a certain load behaves at other loads.
Figure 7.6 (top row) highlights static
robustness of the T1 policy, plotting the mean response time of two T1
policies as a function of  (only
(only  is changed) in
column (a) and as a function of
is changed) in
column (a) and as a function of 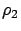 (only
(only 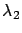 is changed)
in column (b). For example, in column (b),
is changed)
in column (b). For example, in column (b),  is the optimal
threshold when
is the optimal
threshold when  . However, if it turns out that
. However, if it turns out that
 is the actual load, then the T1(3) policy leads to
instability (infinite mean response time), while the T1(19) policy
minimizes mean response time. Thus, choosing a higher
is the actual load, then the T1(3) policy leads to
instability (infinite mean response time), while the T1(19) policy
minimizes mean response time. Thus, choosing a higher  (=19)
guarantees stability against misestimation of
(=19)
guarantees stability against misestimation of 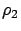 , but results in
worse performance at the estimated load. Similar observation holds
for stability against misestimation of
, but results in
worse performance at the estimated load. Similar observation holds
for stability against misestimation of  (see column (a)),
although the T1 policy appears to have more stability against misestimation
of
(see column (a)),
although the T1 policy appears to have more stability against misestimation
of  than against misestimation of
than against misestimation of 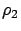 .
Overall, we conclude that the T1
policy optimized at a lower load is poor with respect to static robustness.
While it is possible to tune the T1 policy for higher loads
(by choosing a larger
.
Overall, we conclude that the T1
policy optimized at a lower load is poor with respect to static robustness.
While it is possible to tune the T1 policy for higher loads
(by choosing a larger  ), this would degrade mean response time
at lower loads.
), this would degrade mean response time
at lower loads.
Figure 7.6 (middle row) illustrates the static
robustness of the T2 policy, plotting the mean response time of three
T2 policies as functions of  and
and 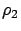 , as in the top row.
In both columns (a) and (b), the T2(2) policy minimizes the mean
response time in the class of T2 policies for a range of loads. That
is,
, as in the top row.
In both columns (a) and (b), the T2(2) policy minimizes the mean
response time in the class of T2 policies for a range of loads. That
is,  is the optimal choice for these parameter settings
(
is the optimal choice for these parameter settings
(
 ) regardless of the loads
(
) regardless of the loads
(
 ). Recall that the T2 policy is optimized at
small
). Recall that the T2 policy is optimized at
small  values (
values (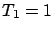 or 2) for a wide range of parameter
settings (see Figures 7.4-7.5). Since the
T2 policy has the widest possible stability region regardless of its
or 2) for a wide range of parameter
settings (see Figures 7.4-7.5). Since the
T2 policy has the widest possible stability region regardless of its  value, its mean response
time is not very sensitive to the changes (or misprediction) in loads
for a wider range of load, as compared to the T1 policy with parameter
value, its mean response
time is not very sensitive to the changes (or misprediction) in loads
for a wider range of load, as compared to the T1 policy with parameter  . In this
sense, the T2 policy has more static robustness than the T1 policy.
. In this
sense, the T2 policy has more static robustness than the T1 policy.
However, Figure 7.6 (bottom) shows that the mean
response time under the optimized T2 policy, T2(2), can be much higher
than that under the T1 policy optimized at each load, which is in
parallel to our previous findings (see Figure 7.5). For
example, in column (b), the mean response time under T2(2) is twice as
high as that under T1(3) when  , and the mean response time
under T2(2) is eight times as high as that under T1(19) when
, and the mean response time
under T2(2) is eight times as high as that under T1(19) when
 . Only at very high
. Only at very high 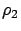 , the mean response time of
T2(2) becomes lower than that of T1(19).
Similar observation holds for column (a) as well.
We conclude that the T2 policy performs worse than the T1 policy
with respect to mean response time.
, the mean response time of
T2(2) becomes lower than that of T1(19).
Similar observation holds for column (a) as well.
We conclude that the T2 policy performs worse than the T1 policy
with respect to mean response time.




Next: Static robustness and mean
Up: Static robustness and mean
Previous: Case 2:
Contents
Takayuki Osogami
2005-07-19
![]() (only
(only ![]() is changed) in
column (a) and as a function of
is changed) in
column (a) and as a function of ![]() (only
(only ![]() is changed)
in column (b). For example, in column (b),
is changed)
in column (b). For example, in column (b), ![]() is the optimal
threshold when
is the optimal
threshold when ![]() . However, if it turns out that
. However, if it turns out that
![]() is the actual load, then the T1(3) policy leads to
instability (infinite mean response time), while the T1(19) policy
minimizes mean response time. Thus, choosing a higher
is the actual load, then the T1(3) policy leads to
instability (infinite mean response time), while the T1(19) policy
minimizes mean response time. Thus, choosing a higher ![]() (=19)
guarantees stability against misestimation of
(=19)
guarantees stability against misestimation of ![]() , but results in
worse performance at the estimated load. Similar observation holds
for stability against misestimation of
, but results in
worse performance at the estimated load. Similar observation holds
for stability against misestimation of ![]() (see column (a)),
although the T1 policy appears to have more stability against misestimation
of
(see column (a)),
although the T1 policy appears to have more stability against misestimation
of ![]() than against misestimation of
than against misestimation of ![]() .
Overall, we conclude that the T1
policy optimized at a lower load is poor with respect to static robustness.
While it is possible to tune the T1 policy for higher loads
(by choosing a larger
.
Overall, we conclude that the T1
policy optimized at a lower load is poor with respect to static robustness.
While it is possible to tune the T1 policy for higher loads
(by choosing a larger ![]() ), this would degrade mean response time
at lower loads.
), this would degrade mean response time
at lower loads.
![]() and
and ![]() , as in the top row.
In both columns (a) and (b), the T2(2) policy minimizes the mean
response time in the class of T2 policies for a range of loads. That
is,
, as in the top row.
In both columns (a) and (b), the T2(2) policy minimizes the mean
response time in the class of T2 policies for a range of loads. That
is, ![]() is the optimal choice for these parameter settings
(
is the optimal choice for these parameter settings
(
![]() ) regardless of the loads
(
) regardless of the loads
(
![]() ). Recall that the T2 policy is optimized at
small
). Recall that the T2 policy is optimized at
small ![]() values (
values (![]() or 2) for a wide range of parameter
settings (see Figures 7.4-7.5). Since the
T2 policy has the widest possible stability region regardless of its
or 2) for a wide range of parameter
settings (see Figures 7.4-7.5). Since the
T2 policy has the widest possible stability region regardless of its ![]() value, its mean response
time is not very sensitive to the changes (or misprediction) in loads
for a wider range of load, as compared to the T1 policy with parameter
value, its mean response
time is not very sensitive to the changes (or misprediction) in loads
for a wider range of load, as compared to the T1 policy with parameter ![]() . In this
sense, the T2 policy has more static robustness than the T1 policy.
. In this
sense, the T2 policy has more static robustness than the T1 policy.
![]() , and the mean response time
under T2(2) is eight times as high as that under T1(19) when
, and the mean response time
under T2(2) is eight times as high as that under T1(19) when
![]() . Only at very high
. Only at very high ![]() , the mean response time of
T2(2) becomes lower than that of T1(19).
Similar observation holds for column (a) as well.
We conclude that the T2 policy performs worse than the T1 policy
with respect to mean response time.
, the mean response time of
T2(2) becomes lower than that of T1(19).
Similar observation holds for column (a) as well.
We conclude that the T2 policy performs worse than the T1 policy
with respect to mean response time.