



Next: Case 2:
Up: Mean response time of
Previous: Mean response time of
Contents
We first consider the case where
 , where
server 2 ``prefers'' to run its own jobs
in a
, where
server 2 ``prefers'' to run its own jobs
in a 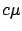 sense. In this
case, we will see that the T1(
sense. In this
case, we will see that the T1( ) policy typically minimizes
mean response time in the class of T1 policies, and the T2(1) policy
typically minimizes mean response time in the class of T2 policies. Note
that the T1(
) policy typically minimizes
mean response time in the class of T1 policies, and the T2(1) policy
typically minimizes mean response time in the class of T2 policies. Note
that the T1( ) policy and the T2(1) policy are identical, and
they also coincide with the policy of
following the
) policy and the T2(1) policy are identical, and
they also coincide with the policy of
following the 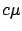 rule when
rule when
 .
Note also that if
.
Note also that if 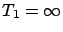 minimizes the mean
response time of the T1 policy,
minimizes the mean
response time of the T1 policy, 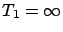 is the optimal choice
with respect to both mean response time and stability region, since
is the optimal choice
with respect to both mean response time and stability region, since
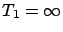 maximizes the stability region of the T1 policy
(see Corollary 4). Likewise, if
maximizes the stability region of the T1 policy
(see Corollary 4). Likewise, if 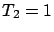 minimizes the
mean response time of the T2 policy,
minimizes the
mean response time of the T2 policy, 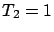 is the optimal choice
with respect to both mean response time and stability region, since
the stability region of the T2 policy is independent of its parameter
is the optimal choice
with respect to both mean response time and stability region, since
the stability region of the T2 policy is independent of its parameter
 (see Theorem 15).
(see Theorem 15).
In fact, when 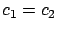 (and
(and
 ),
the following theorems hold (the theorem may extend to the case of
general
),
the following theorems hold (the theorem may extend to the case of
general 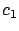 and
and  with
with
 , but the
general case is not proved).
, but the
general case is not proved).
Theorem 16
If 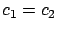 and
and
 , the mean response time
of the T1 policy is minimized at
, the mean response time
of the T1 policy is minimized at 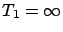 .
.
Proof:Due to Little's law, it is sufficient to prove
that the number of jobs completed under the T1( ) policy
is stochastically larger than those completed under the
T1 policy with
) policy
is stochastically larger than those completed under the
T1 policy with  at any moment.
Let
at any moment.
Let
 be
the joint process of the
number of jobs in queue 1 and queue 2, respectively, at time
be
the joint process of the
number of jobs in queue 1 and queue 2, respectively, at time  when
when 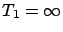 .
Let
.
Let
 be
defined analogously for
be
defined analogously for  .
With
.
With 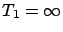 , server 2 processes type
2 jobs as long as there are type 2 jobs, and thus
, server 2 processes type
2 jobs as long as there are type 2 jobs, and thus
 is stochastically larger than
is stochastically larger than
 for all
for all  . Consequently,
the number of jobs completed by sever 1 is stochastically
smaller when
. Consequently,
the number of jobs completed by sever 1 is stochastically
smaller when  than when
than when 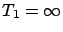 at any moment, since
server 1 is work-conserving.
at any moment, since
server 1 is work-conserving.
As long as server 2 is busy, the number of jobs completed by sever 2
is stochastically smaller when  than when
than when 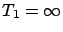 ,
since
,
since
 .
Also, using coupling argument, we can show that the system with
.
Also, using coupling argument, we can show that the system with 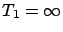 has
server 2 go idle (both queues empty) earlier (stochastically) than the
has
server 2 go idle (both queues empty) earlier (stochastically) than the  system. Thus, when server 2 is idle the number of jobs completed by the
system. Thus, when server 2 is idle the number of jobs completed by the 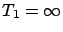 system is stochastically larger.
Thus, the number of jobs
completed (either by server 1 or by server 2) under the T1(
system is stochastically larger.
Thus, the number of jobs
completed (either by server 1 or by server 2) under the T1( ) policy
is stochastically larger than that completed under the
T1 policy with
) policy
is stochastically larger than that completed under the
T1 policy with  . width 1ex height 1ex depth 0pt
. width 1ex height 1ex depth 0pt
Theorem 17
If 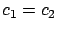 and
and
 , the mean response time
of the T2 policy is minimized at
, the mean response time
of the T2 policy is minimized at 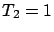 .
.
Theorem 17 can be proved in the same way as
Theorem 16: in the proof of Theorem 17,
the T1 policy with parameter 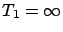 is replaced by the T2 policy
with parameter
is replaced by the T2 policy
with parameter 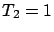 , and the T1 policy with parameter
, and the T1 policy with parameter  is replaced by the T2 policy with parameter
is replaced by the T2 policy with parameter 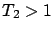 .
.
Further, even when 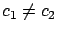 (and
(and
 ), our
analysis of the T1 and T2 policies via DR shows that the T1(
), our
analysis of the T1 and T2 policies via DR shows that the T1( )
policy minimizes mean response time in the class of T1 policies, and
the T2(1) policy minimizes mean response time in the class of T2
policies, for all the cases we have considered.
Figure 7.4 shows a subset of such numerical analyses,
where
)
policy minimizes mean response time in the class of T1 policies, and
the T2(1) policy minimizes mean response time in the class of T2
policies, for all the cases we have considered.
Figure 7.4 shows a subset of such numerical analyses,
where  and
and  are chosen to be the critical case:
are chosen to be the critical case:
 .
In the top half,
.
In the top half, 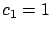 and
and  , and in the bottom half,
, and in the bottom half,  and
and  .
Different columns
correspond to different
.
Different columns
correspond to different 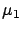 's. In each plot, mean response
time is evaluated at three loads,
's. In each plot, mean response
time is evaluated at three loads,
 , by
changing
, by
changing  .
Although figures are not shown, when
.
Although figures are not shown, when
 , the mean response time under non-optimized T1
and T2 policies becomes much higher than the optimized T1 and T2
policies (T1(
, the mean response time under non-optimized T1
and T2 policies becomes much higher than the optimized T1 and T2
policies (T1( ) and T2(1)), as compared to the case of
) and T2(1)), as compared to the case of
 . This
makes intuitive sense, since non-optimized policies have a bias toward
jobs with smaller
. This
makes intuitive sense, since non-optimized policies have a bias toward
jobs with smaller 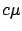 values (less important and/or larger jobs).
values (less important and/or larger jobs).




Next: Case 2:
Up: Mean response time of
Previous: Mean response time of
Contents
Takayuki Osogami
2005-07-19
![]() , where
server 2 ``prefers'' to run its own jobs
in a
, where
server 2 ``prefers'' to run its own jobs
in a ![]() sense. In this
case, we will see that the T1(
sense. In this
case, we will see that the T1(![]() ) policy typically minimizes
mean response time in the class of T1 policies, and the T2(1) policy
typically minimizes mean response time in the class of T2 policies. Note
that the T1(
) policy typically minimizes
mean response time in the class of T1 policies, and the T2(1) policy
typically minimizes mean response time in the class of T2 policies. Note
that the T1(![]() ) policy and the T2(1) policy are identical, and
they also coincide with the policy of
following the
) policy and the T2(1) policy are identical, and
they also coincide with the policy of
following the ![]() rule when
rule when
![]() .
Note also that if
.
Note also that if ![]() minimizes the mean
response time of the T1 policy,
minimizes the mean
response time of the T1 policy, ![]() is the optimal choice
with respect to both mean response time and stability region, since
is the optimal choice
with respect to both mean response time and stability region, since
![]() maximizes the stability region of the T1 policy
(see Corollary 4). Likewise, if
maximizes the stability region of the T1 policy
(see Corollary 4). Likewise, if ![]() minimizes the
mean response time of the T2 policy,
minimizes the
mean response time of the T2 policy, ![]() is the optimal choice
with respect to both mean response time and stability region, since
the stability region of the T2 policy is independent of its parameter
is the optimal choice
with respect to both mean response time and stability region, since
the stability region of the T2 policy is independent of its parameter
![]() (see Theorem 15).
(see Theorem 15).
![]() (and
(and
![]() ),
the following theorems hold (the theorem may extend to the case of
general
),
the following theorems hold (the theorem may extend to the case of
general ![]() and
and ![]() with
with
![]() , but the
general case is not proved).
, but the
general case is not proved).
![]() ) policy
is stochastically larger than those completed under the
T1 policy with
) policy
is stochastically larger than those completed under the
T1 policy with ![]() at any moment.
Let
at any moment.
Let
![]() be
the joint process of the
number of jobs in queue 1 and queue 2, respectively, at time
be
the joint process of the
number of jobs in queue 1 and queue 2, respectively, at time ![]() when
when ![]() .
Let
.
Let
![]() be
defined analogously for
be
defined analogously for ![]() .
With
.
With ![]() , server 2 processes type
2 jobs as long as there are type 2 jobs, and thus
, server 2 processes type
2 jobs as long as there are type 2 jobs, and thus
![]() is stochastically larger than
is stochastically larger than
![]() for all
for all ![]() . Consequently,
the number of jobs completed by sever 1 is stochastically
smaller when
. Consequently,
the number of jobs completed by sever 1 is stochastically
smaller when ![]() than when
than when ![]() at any moment, since
server 1 is work-conserving.
at any moment, since
server 1 is work-conserving.
![]() than when
than when ![]() ,
since
,
since
![]() .
Also, using coupling argument, we can show that the system with
.
Also, using coupling argument, we can show that the system with ![]() has
server 2 go idle (both queues empty) earlier (stochastically) than the
has
server 2 go idle (both queues empty) earlier (stochastically) than the ![]() system. Thus, when server 2 is idle the number of jobs completed by the
system. Thus, when server 2 is idle the number of jobs completed by the ![]() system is stochastically larger.
Thus, the number of jobs
completed (either by server 1 or by server 2) under the T1(
system is stochastically larger.
Thus, the number of jobs
completed (either by server 1 or by server 2) under the T1(![]() ) policy
is stochastically larger than that completed under the
T1 policy with
) policy
is stochastically larger than that completed under the
T1 policy with ![]() . width 1ex height 1ex depth 0pt
. width 1ex height 1ex depth 0pt ![]() (and
(and
![]() ), our
analysis of the T1 and T2 policies via DR shows that the T1(
), our
analysis of the T1 and T2 policies via DR shows that the T1(![]() )
policy minimizes mean response time in the class of T1 policies, and
the T2(1) policy minimizes mean response time in the class of T2
policies, for all the cases we have considered.
Figure 7.4 shows a subset of such numerical analyses,
where
)
policy minimizes mean response time in the class of T1 policies, and
the T2(1) policy minimizes mean response time in the class of T2
policies, for all the cases we have considered.
Figure 7.4 shows a subset of such numerical analyses,
where ![]() and
and ![]() are chosen to be the critical case:
are chosen to be the critical case:
![]() .
In the top half,
.
In the top half, ![]() and
and ![]() , and in the bottom half,
, and in the bottom half, ![]() and
and ![]() .
Different columns
correspond to different
.
Different columns
correspond to different ![]() 's. In each plot, mean response
time is evaluated at three loads,
's. In each plot, mean response
time is evaluated at three loads,
![]() , by
changing
, by
changing ![]() .
Although figures are not shown, when
.
Although figures are not shown, when
![]() , the mean response time under non-optimized T1
and T2 policies becomes much higher than the optimized T1 and T2
policies (T1(
, the mean response time under non-optimized T1
and T2 policies becomes much higher than the optimized T1 and T2
policies (T1(![]() ) and T2(1)), as compared to the case of
) and T2(1)), as compared to the case of
![]() . This
makes intuitive sense, since non-optimized policies have a bias toward
jobs with smaller
. This
makes intuitive sense, since non-optimized policies have a bias toward
jobs with smaller ![]() values (less important and/or larger jobs).
values (less important and/or larger jobs).