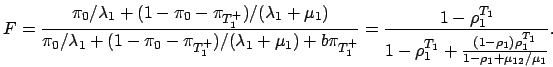|
|
We first consider the stability conditions for the T1 and T2 policies.
In the T1 policy, higher ![]() values yield the larger stability
regions, and in the limit as
values yield the larger stability
regions, and in the limit as
![]() , the queues under
the T1 policy are stable as long as
, the queues under
the T1 policy are stable as long as ![]() and
and ![]() . In
contrast, the T2 policy guarantees stability whenever
. In
contrast, the T2 policy guarantees stability whenever ![]() and
and ![]() for any finite
for any finite ![]() . The T2 policy clearly
dominates the T1 policy in this respect. The stability conditions under
the T1 and T2 policies are illustrated in Figure 7.3.
. The T2 policy clearly
dominates the T1 policy in this respect. The stability conditions under
the T1 and T2 policies are illustrated in Figure 7.3.
More formally, the necessary and sufficient conditions for the stability under the T1 and T2 policies are given by the following theorems.

Proof:We prove only the case when ![]() and
and ![]() . The case when
. The case when ![]() or
or ![]() can be proved in a similar way.
Let
can be proved in a similar way.
Let ![]() be the joint process of the number of jobs in queue
1 and queue 2, respectively. The expected length of a ``busy
period,'' during which
be the joint process of the number of jobs in queue
1 and queue 2, respectively. The expected length of a ``busy
period,'' during which ![]() , is finite if and only if
, is finite if and only if
![]() . This proves the stability condition
for queue 1.
. This proves the stability condition
for queue 1.
Based on the strong law of large numbers,
the necessary and sufficient condition for
stability of queue 2 is ![]() ,
where
,
where ![]() denotes the time average fraction of time that server 2
processes jobs from queue 2 given
denotes the time average fraction of time that server 2
processes jobs from queue 2 given ![]() .
Below, we derive
.
Below, we derive ![]() .
Let
.
Let
![]() be a process
in which
be a process
in which ![]() behaves the same as
behaves the same as ![]() except that
it has no transition from
except that
it has no transition from
![]() to
to
![]() .
Consider a semi-Markov process of
.
Consider a semi-Markov process of
![]() ,
where the state space is (0,1,2,...,
,
where the state space is (0,1,2,...,![]() ,
,![]() ).
The state
).
The state ![]() denotes there are
denotes there are ![]() jobs in queue 1 for
jobs in queue 1 for
![]() ,
and the state
,
and the state ![]() denotes there are at least
denotes there are at least ![]() jobs in queue 1.
The expected sojourn time is
jobs in queue 1.
The expected sojourn time is
![]() for state 0,
for state 0,
![]() for states
for states ![]() ,
and
,
and
![]() for state
for state ![]() ,
where
,
where
![]() is the mean duration of the busy period in an M/M/1 queue with arrival rate
is the mean duration of the busy period in an M/M/1 queue with arrival rate
![]() and service rate
and service rate
![]() .
The limiting probabilities for the corresponding embedded discrete time Markov chain
are
.
The limiting probabilities for the corresponding embedded discrete time Markov chain
are
![]() for
for ![]() and
and
![]() , where
, where