Subclasses of PH distribution

By restricting the structure of the Markov chain, we can define a subclass of the PH distribution. Below, we define subclasses of the PH distribution that come up in this thesis.

Figure 2.8: Subclasses of the PH distribution.

(a) acyclic PH

(b) Coxian PH

(c) generalized Erlang

(d) mixed Erlang

First, if the Markov chain whose absorption time defines a PH distribution is acyclic (i.e., any state is never visited more than once in the Markov chain), the PH distribution is called an acyclic PH distribution. A three-phase acyclic PH distribution is illustrated in Figure 2.8(a) as the absorption time in a Markov chain.

An acyclic PH distribution is called a Coxian PH distribution if the Markov chain whose absorption time defines the acyclic PH distribution has the following two properties: (i) the initial non-absorbing state is unique (i.e., the initial state is either the unique non-absorbing state or the absorbing state), and (ii) for each state, the next non-absorbing state is unique (i.e., the next state is the unique non-absorbing state or the absorbing state). A three-phase Coxian PH distribution is illustrated in Figure 2.8(b). When a Coxian PH distribution does not have mass probability at zero (i.e., the initial state is not the absorbing state), we refer to the Coxian PH distribution as a Coxian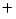$^+$ PH distribution.

An acyclic PH distribution is called a hyperexponential distribution if the Markov chain whose absorption time defines the acyclic PH distribution has the following property: for any state, the next state is the absorbing state. That is, a mixture of exponential distributions is a hyperexponential distribution.

An acyclic PH distribution is called an Erlang distribution if the Markov chain whose absorption time defines the acyclic PH distribution has the following three properties: (i) the initial state is a unique non-absorbing state, (ii) for each state, the next state is unique, and (iii) the sojourn time distribution at each state is identical. That is, the sum of $n$ i.i.d. exponential random variables has an $n$-phase Erlang distribution. An $n$-phase Erlang distribution is also called an Erlang-$n$ distribution. An Erlang distribution is generalized to a generalized Erlang distribution [122] by allowing a transition from the initial state to the absorbing state. A three-phase generalized Erlang distribution is illustrated in Figure 2.8(c).

A mixture of Erlang distributions is called a mixed Erlang distribution [87,88]. A mixed Erlang distribution is illustrated in Figure 2.8(d), where an Erlang-2 distribution and an Erlang-3 distribution are mixed. A mixture of Erlang distributions with the same number of phases, is called a mixed Erlang distribution with common order [87,88].