



Next: State of the art
Up: Brief tutorial on phase
Previous: Subclasses of PH distribution
Contents
Below, we summarize some of the basic properties of the PH distribution.
First, the set of PH distributions is quite broad and,
in theory, any nonnegative distribution can be approximated arbitrarily closely
by a PH distribution.
Proposition 2
[132]
The set of PH distributions is dense in the set of nonnegative distributions (distributions with support on  ).
).
Observe that Proposition 1 follows immediately from Proposition 2.
Second, the set of PH distributions is closed under some operations. In particular,
a mixture of independent PH distributions is a PH distribution,
and the convolution of independent PH distributions is a PH distribution.
Proposition 3
[111]
Consider two PH distributions:
PH(
 ) with distribution function
) with distribution function  and
PH(
and
PH(
 ) with distribution function
) with distribution function  .
A mixture of the two PH distribution, which has distribution function
.
A mixture of the two PH distribution, which has distribution function
 ,
is a PH distribution, PH(
,
is a PH distribution, PH(
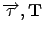 ), where
Here,
), where
Here,  denotes a zero matrix.
denotes a zero matrix.
The convolution of the two PH distributions, PH(
 ) and PH(
) and PH(
 ),
is a PH distribution, PH(
),
is a PH distribution, PH(
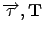 ), where
), where
Here,
 and
and
 , where
, where 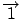 is a column vector of 1's.
is a column vector of 1's.
To shed light on the expression
 ,
consider a random variable
,
consider a random variable  whose distribution function is
whose distribution function is  and a random variable
and a random variable  whose distribution function is
whose distribution function is  .
Then, random variable
.
Then, random variable
has distribution function  .
Below, unless otherwise stated, we denote
the (cumulative) distribution function of a distribution,
.
Below, unless otherwise stated, we denote
the (cumulative) distribution function of a distribution, 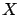 , by
, by  .
.
Definition 9
Let  be a random variable having a distribution
be a random variable having a distribution 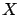 .
We denote the cumulative distribution function by
.
We denote the cumulative distribution function by  , namely
, namely
Finally, the distribution function, the density function, the moments, and the Laplace transform
of a PH distribution have simple mathematical expressions.
Proposition 4
[111]
The distribution function of PH(
 ) is given by
for
) is given by
for  , where the matrix exponential is defined by
, where the matrix exponential is defined by
 .
The density function of PH(
.
The density function of PH(
 ) is given by
for
) is given by
for  ,
where
,
where
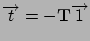 .
.
Let 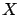 be a random variable with the PH(
be a random variable with the PH(
 ) distribution. Then,
) distribution. Then,
for  .
The Laplace transform of PH(
.
The Laplace transform of PH(
 ) is given by
where
) is given by
where
 and
and  is an identity matrix.
is an identity matrix.




Next: State of the art
Up: Brief tutorial on phase
Previous: Subclasses of PH distribution
Contents
Takayuki Osogami
2005-07-19

![]() ) and PH(
) and PH(
![]() ),
is a PH distribution, PH(
),
is a PH distribution, PH(
![]() ), where
), where


![]() be a random variable with the PH(
be a random variable with the PH(
![]() ) distribution. Then,
) distribution. Then,