



Next: Running time of dimensionality
Up: Validation
Previous: Validation
Contents
Accuracy of dimensionality reduction
In this section, we evaluate the accuracy of DR, DR-PI, and DR-CI.
In all our experiments below, the error in an analysis (DR, DR-PI, or DR-CI)
is defined as a relative difference against simulated value:
Simulation is kept running until the simulation error becomes less
than 1% with probability 0.95 [85,168,193].
More precisely, our simulation keeps generating ``sample values,''
where the  -th ``sample value,''
-th ``sample value,''  , is computed as a sample mean of the metric of interest in the
, is computed as a sample mean of the metric of interest in the  -th run with a
large number (say ten million; this number can be different for different parameter settings) of events,
until one of the following two conditions are satisfied3.8:
(i)
-th run with a
large number (say ten million; this number can be different for different parameter settings) of events,
until one of the following two conditions are satisfied3.8:
(i)  and
and
 , where
, where  and
and  are the sample mean and the sample variance
of the
are the sample mean and the sample variance
of the  ``sample values,'' respectively;
(ii)
``sample values,'' respectively;
(ii)  and
and
 .
Then, the sample mean of the
.
Then, the sample mean of the  ``sample values'' is output as the simulated value.
``sample values'' is output as the simulated value.
Unless otherwise stated, we approximate the ``busy period''
distribution by a two-phase PH distribution. In our parameter
settings, two phases are sufficient to match the first three moments
of the most of the busy periods. Even in a few cases where two phases
are not sufficient, we are able to choose a two phase PH distribution
whose first three moments are very close to those of the busy periods.
Hence, using more phases to match the exact three moments does not
appear to improve the accuracy appreciably.
We first evaluate the error in DR in predicting the mean delay
in the preemptive priority queue. Here, delay of a job denotes
the time the job spends waiting in the queue, i.e. delay does not
include the service time. We choose to evaluate the error in mean delay
rather than the error in mean response time (delay plus service time),
since the error is larger in mean delay.
Figure 3.30:
Accuracy of DR in the analysis of preemptive priority queues.
(a) shows the error in the analysis of an M/M/2 with four
priority classes as a function of load, 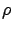 , where the load of class
, where the load of class  is
is  for
each
for
each  .
(b) shows the error in the analysis of
an M/PH/2 with two priority classes as a function of
.
(b) shows the error in the analysis of
an M/PH/2 with two priority classes as a function of
 of the service demands of both high and
low priority jobs, where the total load is fixed at
of the service demands of both high and
low priority jobs, where the total load is fixed at  and the load is
balanced between the classes.
and the load is
balanced between the classes.
|
Error in DR
|
High prio.: small
(
 ) |
|
All same mean
(  ) |
|
High prio.: large
(  ) |
|
(a) M/M/2 with 4 priority classes
|
|
(b) M/PH/2 with 2 priority classes
|
|
Figure 3.30 shows the error in DR in the analysis of
the mean delay in the preemptive priority queue. Column (a) shows
the error in the analysis of an M/M/2 queue with four priority
classes, as a function of load, 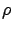 .
(Class 1 is not shown in the figure for clarity, but the analysis of class
1 does not involve DR, and its error is comparable to the error in
classes 2-4.)
The load of each class is
one-quarter of the total load,
.
(Class 1 is not shown in the figure for clarity, but the analysis of class
1 does not involve DR, and its error is comparable to the error in
classes 2-4.)
The load of each class is
one-quarter of the total load, 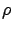 , i.e. each class has the same
load. The service rate of class
, i.e. each class has the same
load. The service rate of class  jobs is set
jobs is set
 for
for
 or 4.
Namely,
or 4.
Namely,  implies small high
priority jobs, and
implies small high
priority jobs, and  implies large high priority jobs. The
three rows in Figure 3.30 correspond to different
values of
implies large high priority jobs. The
three rows in Figure 3.30 correspond to different
values of 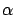 . Column (b) shows the error in
the analysis of an M/PH/2 queue with two priority classes. Here, we
assess the effect of
. Column (b) shows the error in
the analysis of an M/PH/2 queue with two priority classes. Here, we
assess the effect of  , the squared coefficient of variability of
the job size distribution (both the high and low priority jobs),
defined as the variance divided by the square of the mean. The load
of each class is fixed at 0.3, and hence the total load is
, the squared coefficient of variability of
the job size distribution (both the high and low priority jobs),
defined as the variance divided by the square of the mean. The load
of each class is fixed at 0.3, and hence the total load is  .
We use a two phase Coxian
.
We use a two phase Coxian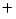 PH distribution (see
Section 2.2) as the job size distribution3.9, where the service rate of class
PH distribution (see
Section 2.2) as the job size distribution3.9, where the service rate of class  jobs is set
jobs is set
 for
for
 or 4 as before.
or 4 as before.
Figure 3.30 shows that the error in DR is within 2%
for all classes, for all 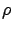 's, for all
's, for all 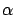 's, and for all
's, and for all  's. On
average, DR tends to underestimate the mean delay only by 0.2% of the
simulation. Overall, the error in DR is quite small in predicting the
first order metric (such as mean delay, mean response time, and mean
queue length). We evaluate the error in DR when it is applied to
other multiserver systems, and find that the error is within
3% in predicting the first order metric for a range of loads,
job size distributions, and other parameters (see
[67,68,70,151,152,155]).
's. On
average, DR tends to underestimate the mean delay only by 0.2% of the
simulation. Overall, the error in DR is quite small in predicting the
first order metric (such as mean delay, mean response time, and mean
queue length). We evaluate the error in DR when it is applied to
other multiserver systems, and find that the error is within
3% in predicting the first order metric for a range of loads,
job size distributions, and other parameters (see
[67,68,70,151,152,155]).
Figure 3.31:
Accuracy of DR, DR-PI, and DR-CI in predicting the first two moments of the queue length distributions,
where 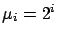 and
and  for each
for each  .
.
|
Error in DR, DR-PI, and DR-CI
|
(a) First moment of queue length
|
|
(b) Second moment of queue length
|
|
Next, we evaluate the accuracy of DR-PI and DR-CI as well as DR in
predicting the first two moments of queue length distributions, through
the analysis of SBCS-ID.
We choose to evaluate the moments of queue length distributions, rather than
delay or response time distributions, since the analysis of higher
moments of delay and response time distributions are complicated,
although possible as we show in Section 3.8.
Throughout, we assume that class  jobs arrive according to a
Poisson process with rate
jobs arrive according to a
Poisson process with rate  , and their service demand has an
exponential distribution with rate
, and their service demand has an
exponential distribution with rate  for
for  .
.
Figure 3.31 shows the error in DR, DR-PI, and DR-CI in
predicting the first two moments of queue length distributions.
Here, we assume that the load made up of each class is fixed
at 0.8 (i.e.
 ), and
), and  is
chosen such that class 1 jobs are the shortest and class
is
chosen such that class 1 jobs are the shortest and class 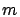 jobs
are the longest, specifically
jobs
are the longest, specifically 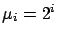 .
Column (a) shows the error in the first moment,
and column (b) shows the error in the second moment.
In the top row, the number of classes (and servers) is
.
Column (a) shows the error in the first moment,
and column (b) shows the error in the second moment.
In the top row, the number of classes (and servers) is
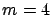 , and all of DR, DR-PI, and DR-CI are evaluated.
In the middle row, the number of servers is
, and all of DR, DR-PI, and DR-CI are evaluated.
In the middle row, the number of servers is  , and
here only DR-PI and DR-CI are evaluated, since evaluation via DR
is computationally too expensive with
, and
here only DR-PI and DR-CI are evaluated, since evaluation via DR
is computationally too expensive with  (see Section 3.9.2).
In the bottom row, the number of servers is
(see Section 3.9.2).
In the bottom row, the number of servers is 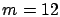 , and here only
DR-CI is evaluated3.10. The horizontal axis
shows the ``server name,'' where server name
, and here only
DR-CI is evaluated3.10. The horizontal axis
shows the ``server name,'' where server name  denotes the
denotes the  -th
server, and hence corresponds to the
-th
server, and hence corresponds to the  -th process. Note that the
scale of the vertical axis is different between (a) and (b).
-th process. Note that the
scale of the vertical axis is different between (a) and (b).
Figure 3.31 shows that the error in DR, DR-PI, and DR-CI
is quite small in predicting the first moment, and it is always within
3%. The error in the second moment is slightly larger, but it is
bounded by 6% for all of DR, DR-PI, and DR-CI. In both the first and
second moments, the error does not appear to increase appreciably as
the number of classes (processes) increases. Top two rows suggest
that DR-PI tends to have only slightly larger error than DR, and DR-CI
tends to have only slightly larger error than DR-PI. The small error
in DR-PI and DR-CI suggests that the duration of the busy period of
server  affects the queue length of server
affects the queue length of server  primarily by the
marginal distribution of the busy period duration, and the dependency
in the sequence of busy period durations has a smaller effect.
primarily by the
marginal distribution of the busy period duration, and the dependency
in the sequence of busy period durations has a smaller effect.
Figure 3.32 shows how the system load affects the accuracy
of RDR in predicting the first two moments of queue length
distributions. Here, the error in DR, DR-PI, DR-CI is plotted at
three different loads,
 , 0.8, or 0.9 for
each
, 0.8, or 0.9 for
each  . Throughout,
. Throughout,  is fixed at
is fixed at 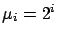 . The figure
suggests that the error in DR, DR-PI, and DR-CI tends to become larger
at higher load. Also, the error in DR-PI and DR-CI tends to become
larger at a slightly faster rate (as the load increases) than the
error in DR. For example, when
. The figure
suggests that the error in DR, DR-PI, and DR-CI tends to become larger
at higher load. Also, the error in DR-PI and DR-CI tends to become
larger at a slightly faster rate (as the load increases) than the
error in DR. For example, when  for
for  , the
error in DR, DR-PI, DR-CI is within 1% (respectively, 2%) in
predicting the first (respectively, second) moment of the queue length
distribution. On the other hand, when
, the
error in DR, DR-PI, DR-CI is within 1% (respectively, 2%) in
predicting the first (respectively, second) moment of the queue length
distribution. On the other hand, when  for
for  , the error in DR is within 3% (respectively, 5%) for the first
(respectively, second) moment, while the error in RDR-PI and RDR-CI is
within 4% (respectively, 7%) for the first (respectively, second)
moment.
, the error in DR is within 3% (respectively, 5%) for the first
(respectively, second) moment, while the error in RDR-PI and RDR-CI is
within 4% (respectively, 7%) for the first (respectively, second)
moment.
Figure 3.32:
Accuracy of DR, DR-PI, and DR-CI at different loads, where 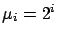 .
.
|
Effect of load in error
|
(a) Second moment of queue length
|
|
(b) First moment of queue length
|
|
Figure 3.33:
Accuracy of DR, DR-PI, and DR-CI at different job size configurations,
where  for each
for each  .
.
|
Effect of job sizes in error
|
(a) First moment of queue length
|
|
(b) Second moment of queue length
|
|
Figure 3.33 shows how the relative difference in the mean
job size of each class affects the accuracy of DR, DR-PI, and DR-CI in predicting the
first two moments of the queue length distribution.
Here, the error in DR, DR-PI, DR-CI is plotted at
four different job size configurations:
 ,
, 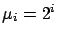 ,
,  , or
, or  .
Throughout,
.
Throughout,  is fixed for
is fixed for  .
Figure suggests that the error
(in predicting both first and second
moments) is greater when idle cycles of the server for longer jobs
is stolen.
We conjecture that this is
primarily due to the fact that the busy period of server
.
Figure suggests that the error
(in predicting both first and second
moments) is greater when idle cycles of the server for longer jobs
is stolen.
We conjecture that this is
primarily due to the fact that the busy period of server  , which
is the sojourn time in levels
, which
is the sojourn time in levels  in the
in the 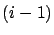 -th process, is
relatively larger as compared to the service time and interarrival
time at server
-th process, is
relatively larger as compared to the service time and interarrival
time at server  if server
if server  is serving longer jobs, and hence the error in
approximating/ignoring the distribution and dependency of the busy
period has larger effect in predicting the queue length distribution
at server
is serving longer jobs, and hence the error in
approximating/ignoring the distribution and dependency of the busy
period has larger effect in predicting the queue length distribution
at server  .
In general the error in DR, DR-PI, and DR-CI
tends to be an increasing function of
.
In general the error in DR, DR-PI, and DR-CI
tends to be an increasing function of 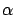 , when
, when
 .
Also, the error
in DR-PI and DR-CI tends to become larger at a slightly faster rate
(as
.
Also, the error
in DR-PI and DR-CI tends to become larger at a slightly faster rate
(as 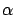 increases) than the error in DR.
For example, when
increases) than the error in DR.
For example, when
 ,
the error in DR, DR-PI, and DR-CI is negligible
in both the first and second moments of the queue length distribution.
On the other hand, when
,
the error in DR, DR-PI, and DR-CI is negligible
in both the first and second moments of the queue length distribution.
On the other hand, when  ,
the error in DR is within 3% (respectively, 7%) in predicting
the first (respectively, second) moment, while the error in DR-PI and
DR-CI is within 6% (respectively, 10%) in predicting the first
(respectively, second) moment.
,
the error in DR is within 3% (respectively, 7%) in predicting
the first (respectively, second) moment, while the error in DR-PI and
DR-CI is within 6% (respectively, 10%) in predicting the first
(respectively, second) moment.
Finally, we study the effect of ignoring higher moments (specifically,
the second and third moments) of the busy period distributions when
they are approximated by PH distributions in DR, DR-PI, and DR-CI.
Figure 3.34 shows the error in DR, DR-PI, and DR-CI
when the busy period distributions are approximated by exponential
distributions matching only the first moments. Other parameter
settings are exactly the same as in Figure 3.31.
Overall, ignoring the variability (and the third moment) of the busy
periods can lead to as high an error as 10% in predicting the first
moment of the queue length distribution and 20% in predicting the
second moment.
Figure 3.34:
Error in DR, DR-PI, and DR-CI when the busy period is approximated by
an exponential distribution matching only the first moment.
|
Error in matching only one moment
|
(a) First moment of queue length
|
|
(b) Second moment of queue length
|
|




Next: Running time of dimensionality
Up: Validation
Previous: Validation
Contents
Takayuki Osogami
2005-07-19
![]() .
(Class 1 is not shown in the figure for clarity, but the analysis of class
1 does not involve DR, and its error is comparable to the error in
classes 2-4.)
The load of each class is
one-quarter of the total load,
.
(Class 1 is not shown in the figure for clarity, but the analysis of class
1 does not involve DR, and its error is comparable to the error in
classes 2-4.)
The load of each class is
one-quarter of the total load, ![]() , i.e. each class has the same
load. The service rate of class
, i.e. each class has the same
load. The service rate of class ![]() jobs is set
jobs is set
![]() for
for
![]() or 4.
Namely,
or 4.
Namely, ![]() implies small high
priority jobs, and
implies small high
priority jobs, and ![]() implies large high priority jobs. The
three rows in Figure 3.30 correspond to different
values of
implies large high priority jobs. The
three rows in Figure 3.30 correspond to different
values of ![]() . Column (b) shows the error in
the analysis of an M/PH/2 queue with two priority classes. Here, we
assess the effect of
. Column (b) shows the error in
the analysis of an M/PH/2 queue with two priority classes. Here, we
assess the effect of ![]() , the squared coefficient of variability of
the job size distribution (both the high and low priority jobs),
defined as the variance divided by the square of the mean. The load
of each class is fixed at 0.3, and hence the total load is
, the squared coefficient of variability of
the job size distribution (both the high and low priority jobs),
defined as the variance divided by the square of the mean. The load
of each class is fixed at 0.3, and hence the total load is ![]() .
We use a two phase Coxian
.
We use a two phase Coxian![]() PH distribution (see
Section 2.2) as the job size distribution3.9, where the service rate of class
PH distribution (see
Section 2.2) as the job size distribution3.9, where the service rate of class ![]() jobs is set
jobs is set
![]() for
for
![]() or 4 as before.
or 4 as before.
![]() 's, for all
's, for all ![]() 's, and for all
's, and for all ![]() 's. On
average, DR tends to underestimate the mean delay only by 0.2% of the
simulation. Overall, the error in DR is quite small in predicting the
first order metric (such as mean delay, mean response time, and mean
queue length). We evaluate the error in DR when it is applied to
other multiserver systems, and find that the error is within
3% in predicting the first order metric for a range of loads,
job size distributions, and other parameters (see
[67,68,70,151,152,155]).
's. On
average, DR tends to underestimate the mean delay only by 0.2% of the
simulation. Overall, the error in DR is quite small in predicting the
first order metric (such as mean delay, mean response time, and mean
queue length). We evaluate the error in DR when it is applied to
other multiserver systems, and find that the error is within
3% in predicting the first order metric for a range of loads,
job size distributions, and other parameters (see
[67,68,70,151,152,155]).
![]() jobs arrive according to a
Poisson process with rate
jobs arrive according to a
Poisson process with rate ![]() , and their service demand has an
exponential distribution with rate
, and their service demand has an
exponential distribution with rate ![]() for
for ![]() .
.
![]() ), and
), and ![]() is
chosen such that class 1 jobs are the shortest and class
is
chosen such that class 1 jobs are the shortest and class ![]() jobs
are the longest, specifically
jobs
are the longest, specifically ![]() .
Column (a) shows the error in the first moment,
and column (b) shows the error in the second moment.
In the top row, the number of classes (and servers) is
.
Column (a) shows the error in the first moment,
and column (b) shows the error in the second moment.
In the top row, the number of classes (and servers) is
![]() , and all of DR, DR-PI, and DR-CI are evaluated.
In the middle row, the number of servers is
, and all of DR, DR-PI, and DR-CI are evaluated.
In the middle row, the number of servers is ![]() , and
here only DR-PI and DR-CI are evaluated, since evaluation via DR
is computationally too expensive with
, and
here only DR-PI and DR-CI are evaluated, since evaluation via DR
is computationally too expensive with ![]() (see Section 3.9.2).
In the bottom row, the number of servers is
(see Section 3.9.2).
In the bottom row, the number of servers is ![]() , and here only
DR-CI is evaluated3.10. The horizontal axis
shows the ``server name,'' where server name
, and here only
DR-CI is evaluated3.10. The horizontal axis
shows the ``server name,'' where server name ![]() denotes the
denotes the ![]() -th
server, and hence corresponds to the
-th
server, and hence corresponds to the ![]() -th process. Note that the
scale of the vertical axis is different between (a) and (b).
-th process. Note that the
scale of the vertical axis is different between (a) and (b).
![]() affects the queue length of server
affects the queue length of server ![]() primarily by the
marginal distribution of the busy period duration, and the dependency
in the sequence of busy period durations has a smaller effect.
primarily by the
marginal distribution of the busy period duration, and the dependency
in the sequence of busy period durations has a smaller effect.
![]() , 0.8, or 0.9 for
each
, 0.8, or 0.9 for
each ![]() . Throughout,
. Throughout, ![]() is fixed at
is fixed at ![]() . The figure
suggests that the error in DR, DR-PI, and DR-CI tends to become larger
at higher load. Also, the error in DR-PI and DR-CI tends to become
larger at a slightly faster rate (as the load increases) than the
error in DR. For example, when
. The figure
suggests that the error in DR, DR-PI, and DR-CI tends to become larger
at higher load. Also, the error in DR-PI and DR-CI tends to become
larger at a slightly faster rate (as the load increases) than the
error in DR. For example, when ![]() for
for ![]() , the
error in DR, DR-PI, DR-CI is within 1% (respectively, 2%) in
predicting the first (respectively, second) moment of the queue length
distribution. On the other hand, when
, the
error in DR, DR-PI, DR-CI is within 1% (respectively, 2%) in
predicting the first (respectively, second) moment of the queue length
distribution. On the other hand, when ![]() for
for ![]() , the error in DR is within 3% (respectively, 5%) for the first
(respectively, second) moment, while the error in RDR-PI and RDR-CI is
within 4% (respectively, 7%) for the first (respectively, second)
moment.
, the error in DR is within 3% (respectively, 5%) for the first
(respectively, second) moment, while the error in RDR-PI and RDR-CI is
within 4% (respectively, 7%) for the first (respectively, second)
moment.
![]() ,
, ![]() ,
, ![]() , or
, or ![]() .
Throughout,
.
Throughout, ![]() is fixed for
is fixed for ![]() .
Figure suggests that the error
(in predicting both first and second
moments) is greater when idle cycles of the server for longer jobs
is stolen.
We conjecture that this is
primarily due to the fact that the busy period of server
.
Figure suggests that the error
(in predicting both first and second
moments) is greater when idle cycles of the server for longer jobs
is stolen.
We conjecture that this is
primarily due to the fact that the busy period of server ![]() , which
is the sojourn time in levels
, which
is the sojourn time in levels ![]() in the
in the ![]() -th process, is
relatively larger as compared to the service time and interarrival
time at server
-th process, is
relatively larger as compared to the service time and interarrival
time at server ![]() if server
if server ![]() is serving longer jobs, and hence the error in
approximating/ignoring the distribution and dependency of the busy
period has larger effect in predicting the queue length distribution
at server
is serving longer jobs, and hence the error in
approximating/ignoring the distribution and dependency of the busy
period has larger effect in predicting the queue length distribution
at server ![]() .
In general the error in DR, DR-PI, and DR-CI
tends to be an increasing function of
.
In general the error in DR, DR-PI, and DR-CI
tends to be an increasing function of ![]() , when
, when
![]() .
Also, the error
in DR-PI and DR-CI tends to become larger at a slightly faster rate
(as
.
Also, the error
in DR-PI and DR-CI tends to become larger at a slightly faster rate
(as ![]() increases) than the error in DR.
For example, when
increases) than the error in DR.
For example, when
![]() ,
the error in DR, DR-PI, and DR-CI is negligible
in both the first and second moments of the queue length distribution.
On the other hand, when
,
the error in DR, DR-PI, and DR-CI is negligible
in both the first and second moments of the queue length distribution.
On the other hand, when ![]() ,
the error in DR is within 3% (respectively, 7%) in predicting
the first (respectively, second) moment, while the error in DR-PI and
DR-CI is within 6% (respectively, 10%) in predicting the first
(respectively, second) moment.
,
the error in DR is within 3% (respectively, 7%) in predicting
the first (respectively, second) moment, while the error in DR-PI and
DR-CI is within 6% (respectively, 10%) in predicting the first
(respectively, second) moment.