



Next: Static robustness of the
Up: Static robustness and mean
Previous: T1T2 policy
Contents
The adaptive dual threshold (ADT) policy
The key idea in the design of the ADT policy is that, in contrast to
the T1T2 policy, the ADT policy is always operating as a T1
policy, but unlike the standard T1 policy, the value of  adapts,
depending on the length of queue 2, to provide static robustness.
Specifically, the ADT policy
behaves like the T1 policy with parameter
adapts,
depending on the length of queue 2, to provide static robustness.
Specifically, the ADT policy
behaves like the T1 policy with parameter  if the length of queue 2 is
less than
if the length of queue 2 is
less than  and otherwise like the T1 policy with parameter
and otherwise like the T1 policy with parameter 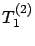 , where
, where
 .
.
We will see that the ADT policy, unlike the T1T2 policy, is far superior to the T1 policy with
respect to static robustness, due to the dual thresholds on queue 1.
In addition, one might also expect that the mean response time of the
optimized ADT policy will significantly improve upon that of the optimized T1
policy, since the ADT policy generalizes the T1 policy (the ADT policy
is reduced to the T1 policy by setting
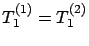 ).
However, this turns out to be largely false, as we see below.
Formally, the ADT policy is characterized by the following rule.
).
However, this turns out to be largely false, as we see below.
Formally, the ADT policy is characterized by the following rule.
Definition 19
The ADT policy with parameters (
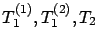 )
operates as the T1 policy with parameter
)
operates as the T1 policy with parameter  if
if  ;
otherwise, it operates as the T1 policy with parameter
;
otherwise, it operates as the T1 policy with parameter 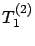 .
.
Below, the ADT policy with parameters (
 ) is also
denoted by the ADT(
) is also
denoted by the ADT(
 ) policy.
) policy.
Figure 7.9:
Figure shows whether server 2 works on jobs from queue 1 or queue 2 as
a function of  and
and
 under the ADT policy with parameters
under the ADT policy with parameters
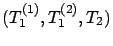 .
.
|
|
Figure 7.9 shows the jobs processed by server 2 under
the ADT policy as a function of  and
and  . At high enough
. At high enough
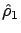 and
and 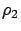 ,
,  usually exceeds
usually exceeds  , and the policy
behaves similar to the T1 policy with parameter
, and the policy
behaves similar to the T1 policy with parameter 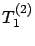 . Thus, the stability
condition for the ADT policy is the same as
that for the T1 policy with parameter
. Thus, the stability
condition for the ADT policy is the same as
that for the T1 policy with parameter 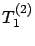 . The following theorem can be
proved in a similar way as Theorem 14.
. The following theorem can be
proved in a similar way as Theorem 14.
Theorem 19
The stability condition for the ADT policy with parameters (
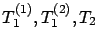 )
is given by the stability condition for the T1 policy with parameter
)
is given by the stability condition for the T1 policy with parameter 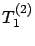 (Theorem 14).
(Theorem 14).
Subsections




Next: Static robustness of the
Up: Static robustness and mean
Previous: T1T2 policy
Contents
Takayuki Osogami
2005-07-19
![]() adapts,
depending on the length of queue 2, to provide static robustness.
Specifically, the ADT policy
behaves like the T1 policy with parameter
adapts,
depending on the length of queue 2, to provide static robustness.
Specifically, the ADT policy
behaves like the T1 policy with parameter ![]() if the length of queue 2 is
less than
if the length of queue 2 is
less than ![]() and otherwise like the T1 policy with parameter
and otherwise like the T1 policy with parameter ![]() , where
, where
![]() .
.
![]() ).
However, this turns out to be largely false, as we see below.
Formally, the ADT policy is characterized by the following rule.
).
However, this turns out to be largely false, as we see below.
Formally, the ADT policy is characterized by the following rule.
![\includegraphics[width=.3\linewidth]{Robust/ADTpolicy.eps}](img1684.png)