Rectangular Surface Parameterization
 Corman,
Crane
Corman,
Crane
ACM Trans. on Graph. (2025)
Abstract
This paper describes a method for computing surface parameterizations that map infinitesimal axis-aligned squares in the plane to infinitesimal rectangles on the surface. Such rectangular parameterizations are needed for a broad range of tasks, from physical simulation to geometric modeling to computational fabrication. Our main contribution is a novel strategy for constructing frame fields that are perfectly orthogonal and exactly integrable, in the limit of mesh refinement. In contrast to past strategies for achieving integrability, we obtain maps that are less distorted and better preserve target field directions. The method supports user-defined distortion measures, sharp feature alignment, prescribed or automatic cone singularities, and direct control over boundary behavior (e.g.,, sizing or aspect ratio). By quantizing and contouring these maps we obtain high-quality anisotropic quad meshes, even without element-based optimization. Empirically, we outperform state-of-the-art research and commercial mesh generation algorithms in terms of element quality, accuracy, and asymptotic convergence rate in end-to-end simulation tasks, are competitive with the widely-used ZBrush package for automatic retopology, and provide Chebyshev nets of superior quality to methods specifically tailored to digital fabrication.
PDF
Supplement
BibTeX
@article{Corman:2025:RSP,
author = {Corman, Etienne and Crane, Keenan},
title = {Rectangular Surface Parameterization},
journal = {ACM Trans. Graph.},
volume = {44},
number = {4},
year = {2025},
publisher = {ACM},
address = {New York, NY, USA},
}
Best Paper (Honorable Mention)
Solving
Partial Differential Equations
in Participating Media
 Miller,
Sawhney,
Crane
Gkioulekas
Miller,
Sawhney,
Crane
Gkioulekas
ACM Trans. on Graph. (2025)
Abstract
We consider the problem of solving partial differential equations (PDEs) in domains with complex microparticle geometry that is impractical, or intractable, to model explicitly. Drawing inspiration from volume rendering, we propose tackling this problem by treating the domain as a participating medium that models microparticle geometry stochastically, through aggregate statistical properties (e.g., particle density). We first introduce the problem setting of PDE simulation in participating media. We then specialize to exponential media and describe the properties that make them an attractive model of microparticle geometry for PDE simulation problems. We use these properties to develop two new algorithms, volumetric walk on spheres and volumetric walk on stars, that generalize previous Monte Carlo algorithms to enable efficient and discretization-free simulation of linear elliptic PDEs (e.g., Laplace) in participating media. We demonstrate experimentally that our algorithms can solve Laplace boundary value problems with complex microparticle geometry more accurately and more efficiently than previous approaches, such as ensemble averaging and homogenization.
PDF
Project
BibTeX
@article{Miller:2025:PRB,
author = {Miller, Bailey and Sawhney, Rohan and Crane, Keenan and Gkioulekas, Ioannis},
title = {Solving Partial Differential Equations in Participating Media},
journal = {ACM Trans. Graph.},
volume = {44},
number = {4},
year = {2025},
publisher = {ACM},
address = {New York, NY, USA},
}
Putting Rigid Bodies to Rest
 Baktash,
Sharp,
Zhou,
Crane,
Jacobson
Baktash,
Sharp,
Zhou,
Crane,
Jacobson
ACM Trans. on Graph. (2025)
Abstract
This paper explores the analysis and design of the resting configurations of a rigid body, without the use of physical simulation. In particular, given a rigid body in ℝ³, we identify all possible stationary points, as well as the probability that the body will stop at these points, assuming a random initial orientation and negligible momentum. The forward version of our method can hence be used to automatically orient models, to provide feedback about object stability during the design process, and to furnish plausible distributions of shape orientation for natural scene modeling. Moreover, a differentiable inverse version of our method lets us design shapes with target resting behavior, such as dice with target, nonuniform probabilities. Here we find solutions that would be nearly impossible to find using classical techniques, such as dice with additional unstable faces that provide more natural overall geometry.
PDF
Data
BibTeX
@article{Baktash:2025:PRB,
author = {Baktash, Hossein and Sharp, Nicholas and Zhou, Qingnan and Crane, Keenan and Jacobson, Alec},
title = {Putting Rigid Bodies to Rest},
journal = {ACM Trans. Graph.},
volume = {44},
number = {4},
year = {2025},
publisher = {ACM},
address = {New York, NY, USA},
}
State of the Art in
Grid-Free Monte Carlo Methods
for Partial Differential Equations
 Sawhney,
Miller,
Gkioulekas,
Crane
Sawhney,
Miller,
Gkioulekas,
Crane
SIGGRAPH Courses (2025)
Abstract
This 3 hour course provides a detailed overview of grid-free Monte Carlo methods for solving partial differential equations (PDEs) based on the walk on spheres (WoS) algorithm, with a special emphasis on problems with high geometric complexity. PDEs are a basic building block of models and algorithms used throughout science, engineering and visual computing. Yet despite decades of research, conventional PDE solvers struggle to capture the immense geometric complexity of the natural world. A perennial challenge is spatial discretization: traditionally, one must partition the domain into a high-quality volumetric mesh—a process that can be brittle, memory intensive, and difficult to parallelize. WoS makes a radical departure from this approach, by reformulating the problem in terms of recursive integral equations that can be estimated using the Monte Carlo method, eliminating the need for spatial discretization. Since these equations strongly resemble those found in light transport theory, one can leverage deep knowledge from Monte Carlo rendering to develop new PDE solvers that share many of its advantages: no meshing, trivial parallelism, and the ability to evaluate the solution at any point without solving a global system of equations.
The course is divided into two parts. Part I will cover the basics of using WoS to solve fundamental PDEs like the Poisson equation. Topics include formulating the solution as an integral equation, generating samples via recursive random walks, and employing accelerated distance and ray intersection queries to efficiently handle complex geometries. Participants will also gain experience setting up demo applications involving data interpolation, heat transfer, and geometric optimization using the open-source “Zombie” library, which implements various grid-free Monte Carlo PDE solvers. Part II will feature a mini-panel of academic and industry contributors covering advanced topics including variance reduction, differentiable and multi-physics simulation, and applications in industrial design and robust geometry processing.
Project
HTML
BibTeX
@inproceedings{sawhney2025state,
title={State of the Art in Grid-Free Monte Carlo Methods for Partial Differential Equations},
author={Sawhney, Rohan and Miller, Bailey and Gkioulekas, Ioannis and Crane, Keenan},
booktitle={Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference Courses},
pages={1--8},
year={2025}
}
Differential Walk on Spheres
 Miller,
Sawhney,
Crane,
Gkioulekas
Miller,
Sawhney,
Crane,
Gkioulekas
ACM Trans. on Graph. (2024)
Abstract
We introduce a Monte Carlo method for evaluating derivatives of the solution to a partial differential equation (PDE) with respect to problem parameters (such as domain geometry or boundary conditions). Derivatives can be evaluated at arbitrary points without performing a global solve, or constructing a volumetric grid or mesh. The method is hence well-suited to inverse problems with complex geometry, such as PDE-constrained shape optimization. Like other walk on spheres (WoS) algorithms, our method is trivial to parallelize, and is agnostic to boundary representation (meshes, splines, implicit surfaces, etc.), supporting large topological changes. We focus in particular on screened Poisson equations, which model diverse problems from scientific and geometric computing. As in differentiable rendering, we jointly estimate derivatives with respect to all parameters—hence, cost does not grow significantly with parameter count. In practice, even noisy derivative estimates exhibit fast, stable convergence for stochastic gradient-based optimization—as we show via examples from thermal design, shape from diffusion, and computer graphics.
Project
PDF
BibTeX
@article{Miller:2024:DWS,
author = {DWS},
title = {Differential Walk on Spheres},
journal = {ACM Trans. Graph.},
volume = {43},
number = {6},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Ray Tracing
Harmonic Functions
 Gillespie,
Yang,
Botsch,
Crane
Gillespie,
Yang,
Botsch,
Crane
ACM Trans. on Graph. (2024)
Abstract
The sphere tracing algorithm provides a fast and high-quality strategy for visualizing surfaces encoded by signed distance functions (SDFs), which have become a centerpiece in a wide range of visual computing algorithms. In this paper we introduce a sphere tracing algorithm for a completely different class of functions, harmonic functions, opening up a whole new set of possibilities. Harmonic functions are found throughout geometric and visual computing, where they arise naturally as the solution to interpolation problems, and in the physical sciences, where they appear as solutions to the Laplace equation. Our algorithm for harmonic functions is similar in spirit to the sphere tracing algorithm for SDFs: by using a conservative lower bound on the distance to the level set, we can take much larger steps than with naïve ray marching. Our key observation is that for harmonic functions such a bound is given by Harnack's inequality. Unlike Lipschitz bounds used in traditional sphere tracing, this Harnack bound requires only the value of the function at a point—we use this bound to develop a sphere tracing algorithm that can also handle jump discontinuities arising in angle-based harmonic functions. We show how this algorithm can be used to directly visualize smooth surfaces reconstructed from point clouds (via Poisson surface reconstruction) or polygon soup (via generalized winding numbers) without performing linear solves or mesh extraction. We also show how it can be used to render nonplanar polygons (including those with holes), and to visualize key objects from mathematics, including knots, links, spherical harmonics, and Riemann surfaces.
PDF
Project
BibTeX
@article{Gillespie:2024:RTH,
author = {Gillespie, Mark and Yang, Denise and Botsch, Mario and Crane, Keenan},
title = {Ray Tracing Harmonic Functions},
journal = {ACM Trans. Graph.},
volume = {43},
number = {4},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Best Paper (Honorable Mention)
Repulsive Shells
 Sassen,
Schumacher,
Rumpf,
Crane
Sassen,
Schumacher,
Rumpf,
Crane
ACM Trans. on Graph. (2024)
Abstract
This paper develops a shape space framework for collision-aware geometric modeling, where basic geometric operations automatically avoid interpenetration. Shape spaces are a powerful tool for surface modeling, shape analysis, nonrigid motion planning, and animation, but past formulations permit nonphysical intersections. Our framework augments an existing shape space using a repulsive energy such that collision avoidance becomes a first-class property, encoded in the Riemannian metric itself. In turn, tasks like intersection-free shape interpolation or motion extrapolation amount to simply computing geodesic paths via standard numerical algorithms. To make optimization practical, we develop an adaptive collision penalty that prevents mesh self-intersection, and converges to a meaningful limit energy under refinement. The final algorithms apply to any category of shape, and do not require a dataset of examples, training, rigging, nor any other prior information. For instance, to interpolate between two shapes we need only a single pair of meshes with the same connectivity. We evaluate our method on a variety of challenging examples from modeling and animation.
PDF
Project
BibTeX
@article{Sassen:2024:RS,
author = {Sassen, Josua and Schumacher, Henrik and Rumpf, Martin and Crane, Keenan},
title = {Repulsive Shells},
journal = {ACM Trans. Graph.},
volume = {43},
number = {4},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Best Paper Award
Walkin' Robin:
Walk on Stars with
Robin Boundary Conditions
 Miller,
Sawhney,
Crane,
Gkioulekas
Miller,
Sawhney,
Crane,
Gkioulekas
ACM Trans. on Graph. (2024)
Abstract
Numerous scientific and engineering applications require solutions to boundary value problems (BVPs) involving elliptic partial differential equations, such as the Laplace or Poisson equations, on geometrically intricate domains. We develop a Monte Carlo method for solving such BVPs with arbitrary first-order linear boundary conditions—Dirichlet, Neumann, and Robin. Our method directly generalizes the walk on stars (WoSt) algorithm, which previously tackled only the first two types of boundary conditions, with a few simple modifications. Unlike conventional numerical methods, WoSt does not need finite element meshing or global solves. Similar to Monte Carlo rendering, it instead computes pointwise solution estimates by simulating random walks along star-shaped regions inside the BVP domain, using efficient ray-intersection and distance queries. To ensure WoSt produces bounded-variance estimates in the presence of Robin boundary conditions, we show that it is sufficient to modify how WoSt selects the size of these star-shaped regions. Our generalized WoSt algorithm reduces estimation error by orders of magnitude relative to alternative grid-free methods such as the walk on boundary algorithm. We also develop bidirectional and boundary value caching strategies to further reduce estimation error. Our algorithm is trivial to parallelize, scales sublinearly with increasing geometric detail, and enables progressive and view-dependent evaluation.
Project
PDF
BibTeX
@article{Miller:2024:WRW,
author = {Miller, Bailey and Sawhney, Rohan and Crane, Keenan and Gkioulekas, Ioannis},
title = {Walkin' Robin: Walk on Stars with Robin Boundary Conditions},
journal = {ACM Trans. Graph.},
volume = {43},
number = {4},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Best Paper Award
A Heat Method for
Generalized Signed Distance
 Feng,
Crane
Feng,
Crane
ACM Trans. on Graph. (2024)
Abstract
We introduce a method for approximating the signed distance function (SDF) of geometry corrupted by holes, noise, or self-intersections. The method implicitly defines a completed version of the shape, rather than explicitly repairing the given input. Our starting point is a modified version of the heat method for geodesic distance, which diffuses normal vectors rather than a scalar distribution. This formulation provides robustness akin to generalized winding numbers (GWN), but provides distance function rather than just an inside/outside classification. Our formulation also offers several features not common to classic distance algorithms, such as the ability to simultaneously fit multiple level sets, a notion of distance for geometry that does not topologically bound any region, and the ability to mix and match signed and unsigned distance. The method can be applied in any dimension and to any spatial discretization, including triangle meshes, tet meshes, point clouds, polygonal meshes, voxelized surfaces, and regular grids. We evaluate the method on several challenging examples, implementing normal offsets and other morphological operations directly on imperfect curve and surface data. In many cases we also obtain an inside/outside classification dramatically more robust than the one obtained provided by GWN.
PDF
Project
BibTeX
@article{Feng:2024:HMG,
author = {Feng, Nicole and Crane, Keenan},
title = {A Heat Method for Generalized Signed Distance},
journal = {ACM Trans. Graph.},
volume = {43},
number = {4},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Minkowski Penalties: Robust
Differentiable Constraint
Enforcement for Vector Graphics
 Minarčík,
Estep,
Ni,
Crane
Minarčík,
Estep,
Ni,
Crane
SIGGRAPH 2024
Abstract
This paper describes an optimization-based framework for finding arrangements of 2D shapes subject to pairwise constraints. Such arrangements naturally arise in tasks such as vector illustration and diagram generation, but enforcing these criteria robustly is surprisingly challenging. We approach this problem through the minimization of novel energetic penalties, derived from the signed distance function of the Minkowski difference between interacting shapes. This formulation provides useful gradients even when initialized from a wildly infeasible state, and, unlike many common collision penalties, can handle open curves that do not have a well-defined inside and outside. Moreover, it supports rich features beyond the basic no-overlap condition, such as tangency, containment, and precise padding, which are especially valuable in the vector illustration context. We develop closed-form expressions and efficient approximations of our penalty for standard vector graphics primitives, yielding efficient evaluation and easy implementation within existing automatic differentiation pipelines. The method has already been “battle-tested” as a component of public-facing open source software; we demonstrate the utility of the framework via examples from illustration, data visualization, diagram generation, and geometry processing.
PDF
Project
BibTeX
@article{Minarcik:2024:MPR,
author = {Minar\v{c}\'{i}k, Ji\v{r}i and Estep, Sam and Ni, Wode and Crane, Keenan},
title = {Minkowski Penalties: Robust Differentiable Constraint Enforcement for Vector Graphics},
journal = {ACM SIGGRAPH 2024 Conference Proceedings},
volume = {43},
number = {4},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
I❤️Mesh: A DSL
for Mesh Processing
 Li,
Kamil,
Crane,
Jacobson,
Gingold
Li,
Kamil,
Crane,
Jacobson,
Gingold
ACM Trans. on Graph. (2024)
Abstract
Mesh processing algorithms are often communicated via concise mathematical notation (e.g., summation over mesh neighborhoods). However, conversion of notation into working code remains a time consuming and error-prone process which requires arcane knowledge of low-level data structures and libraries—impeding rapid exploration of high-level algorithms. We address this problem by introducing a domain-specific language (DSL) for mesh processing called I❤️️️MESH, which resembles notation commonly used in visual and geometric computing, and automates the process of converting notation into code. The centerpiece of our language is a flexible notation for specifying and manipulating neighborhoods of a cell complex, internally represented via standard operations on sparse boundary matrices. This layered design enables natural expression of algorithms while minimizing demands on a code generation back-end. In particular, by integrating I❤️️️MESH with the linear algebra features of the I❤️️️LA DSL, and adding support for automatic differentiation, we can rapidly implement a rich variety of algorithms on point clouds, surface meshes, and volume meshes.
PDF
Project
BibTeX
@article{Li:2024:IHM,
author = {Li, Yong and Kamil, Shoaib and Crane, Keenan and Jacobson, Alec and Gingold, Yotam},
title = {I$\heartsuit$Mesh: A DSL for Mesh Processing},
journal = {ACM Trans. Graph.},
volume = {43},
number = {6},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}
Walk on Stars: A Grid-Free Monte
Carlo Method for PDEs with
Neumann Boundary Conditions
 Sawhney,
Miller,
Gkioulekas,
Crane
Sawhney,
Miller,
Gkioulekas,
Crane
ACM Trans. on Graph. (2023)
Abstract
Grid-free Monte Carlo methods based on the walk on spheres (WoS) algorithm solve fundamental partial differential equations (PDEs) like the Poisson equation without discretizing the problem domain or approximating functions in a finite basis. Such methods hence avoid aliasing in the solution, and evade the many challenges of mesh generation. Yet for problems with complex geometry, practical grid-free methods have been largely limited to basic Dirichlet boundary conditions. This paper introduces the walk on stars (WoSt) method, which solves linear elliptic PDEs with arbitrary mixed Neumann and Dirichlet boundary conditions. The key insight is that one can efficiently simulate reflecting Brownian motion (which models Neumann conditions) by replacing the balls used by WoS with star-shaped domains; we identify such domains by locating the closest visible point on the geometric silhouette. Overall, WoSt retains many attractive features of other grid-free Monte Carlo methods, such as progressive and view-dependent evaluation, trivial parallelization, and sublinear scaling to increasing geometric detail.
PDF
Project
BibTeX
@article{Sawhney:2023:WoSt,
author = {Sawhney, Rohan and Miller, Bailey and Gkioulekas, Ioannis and Crane, Keenan},
title = {Walk on Stars: A Grid-Free Monte Carlo Method for PDEs with Neumann Boundary Conditions},
journal = {ACM Trans. Graph.},
volume = {42},
number = {4},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
}
Winding Numbers on
Discrete Surfaces
 Feng,
Gillespie,
Crane
Feng,
Gillespie,
Crane
ACM Trans. on Graph. (2023)
Abstract
In the plane, the winding number is the number of times a curve wraps around a given point. Winding numbers are a basic component of geometric algorithms such as point-in-polygon tests, and their generalization to data with noise or topological errors has proven valuable for geometry processing tasks ranging from surface reconstruction to mesh booleans. However, standard definitions do not immediately apply on surfaces, where not all curves bound regions. We develop a meaningful generalization, starting with the well-known relationship between winding numbers and harmonic functions. By processing the derivatives of such functions, we can robustly filter out components of the input that do not bound any region. Ultimately, our algorithm yields (i) a closed, completed version of the input curves, (ii) integer labels for regions that are meaningfully bounded by these curves, and (iii) the complementary curves that do not bound any region. The main computational cost is solving a standard Poisson equation, or for surfaces with nontrivial topology, a sparse linear program. We also introduce special basis functions to represent singularities that naturally occur at endpoints of open curves.
PDF
Project
BibTeX
@article{Feng:2023:WND,
author = {Feng, Nicole and Gillespie, Mark and Crane, Keenan},
title = {Winding Numbers on Discrete Surfaces},
journal = {ACM Trans. Graph.},
volume = {42},
number = {4},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
}
Boundary Value Caching
for Walk on Spheres
 Miller,
Sawhney,
Crane,
Gkioulekas
Miller,
Sawhney,
Crane,
Gkioulekas
ACM Trans. on Graph. (2023)
Abstract
Grid-free Monte Carlo methods such as walk on spheres can be used to solve elliptic partial differential equations without mesh generation or global solves. However, such methods independently estimate the solution at every point, and hence do not take advantage of the high spatial regularity of solutions to elliptic problems. We propose a fast caching strategy which first estimates solution values and derivatives at randomly sampled points along the boundary of the domain (or a local region of interest). These cached values then provide cheap, output-sensitive evaluation of the solution (or its gradient) at interior points, via a boundary integral formulation. Unlike classic boundary integral methods, our caching scheme introduces zero statistical bias and does not require a dense global solve. Moreover we can handle imperfect geometry (e.g., with self-intersections) and detailed boundary/source terms without repairing or resampling the boundary representation. Overall, our scheme is similar in spirit to virtual point light methods from photorealistic rendering: it suppresses the typical salt-and-pepper noise characteristic of independent Monte Carlo estimates, while still retaining the many advantages of Monte Carlo solvers: progressive evaluation, trivial parallelization, geometric robustness, etc. We validate our approach using test problems from visual and geometric computing.
PDF
BibTeX
@article{Miller:2023:BVC,
author = {Miller, Bailey and Sawhney, Rohan and Crane, Keenan and Gkioulekas, Ioannis},
title = {Boundary Value Caching for Walk on Spheres},
journal = {ACM Trans. Graph.},
volume = {42},
number = {4},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
}
Surface Simplification using
Intrinsic Error Metrics
 Liu,
Gillespie,
Chislett,
Liu,
Gillespie,
Chislett,
Sharp,
Jacobson,
Crane
ACM Trans. on Graph. (2023)
Abstract
This paper describes a method for fast simplification of surface meshes. Whereas past methods focus on visual appearance, our goal is to solve equations on the surface. Hence, rather than approximate the extrinsic geometry, we construct a coarse intrinsic triangulation of the input domain. In the spirit of the quadric error metric (QEM), we perform greedy decimation while agglomerating global information about approximation error. In lieu of extrinsic quadrics, however, we store intrinsic tangent vectors that track how far curvature “drifts” during simplification. This process also yields a bijective map between the fine and coarse mesh, and prolongation operators for both scalar- and vector-valued data. Moreover, we obtain hard guarantees on element quality via intrinsic retriangulation—a feature unique to the intrinsic setting. The overall payoff is a “black box” approach to geometry processing, which decouples mesh resolution from the size of matrices used to solve equations. We show how our method benefits several fundamental tasks, including geometric multigrid, all-pairs geodesic distance, mean curvature flow, geodesic Voronoi diagrams, and the discrete exponential map.
PDF
BibTeX
@article{Liu:2023:SSI,
author = {Liu, Derek and Gillespie, Mark and Chislett, Benjamin and Sharp, Nicholas and Jacobson, Alec and Crane, Keenan},
title = {Surface Simplification using Intrinsic Error Metrics},
journal = {ACM Trans. Graph.},
volume = {42},
number = {4},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
}
Grid-Free Monte Carlo
for PDEs with Spatially
Varying Coefficients
 Sawhney,
Seyb,
Jarosz,
Crane
Sawhney,
Seyb,
Jarosz,
Crane
ACM Trans. on Graph. (2022)
Abstract
Partial differential equations (PDEs) with spatially varying coefficients arise throughout science and engineering, modeling rich heterogeneous material behavior. Yet conventional PDE solvers struggle with the immense complexity found in nature, since they must first discretize the problem—leading to spatial aliasing, and global meshing/sampling that is costly and error-prone. We describe a method that approximates neither the domain geometry, the problem data, nor the solution space, providing the exact solution (in expectation) even for problems with extremely detailed geometry and intricate coefficients. Our main contribution is to extend the walk on spheres (WoS) algorithm from constant- to variable-coefficient problems, by drawing on techniques from volumetric rendering. In particular, an approach inspired by null-scattering yields unbiased Monte Carlo estimators for a large class of 2nd order elliptic PDEs, which share many attractive features with Monte Carlo rendering: no meshing, trivial parallelism, and the ability to evaluate the solution at any point without solving a global system of equations.
PDF
Project
BibTeX
@article{Sawhney:2022:DND,
author = {Sawhney, Rohan and Seyb, Dario and Jarosz, Wojciech and Crane, Keenan},
title = {Grid-Free Monte Carlo for PDEs with Spatially Varying Coefficients},
journal = {ACM Trans. Graph.},
volume = {XX},
number = {X},
year = {2022},
publisher = {ACM},
address = {New York, NY, USA},
}
DiffusionNet: Discretization
Agnostic Learning on Surfaces
 Sharp,
Attaiki,
Crane,
Ovsjanikov
Sharp,
Attaiki,
Crane,
Ovsjanikov
ACM Trans. on Graph. (2022)
Abstract
We introduce a new approach to deep learning on 3D surfaces, based on the insight that a simple diffusion layer is highly effective for spatial communication. The resulting networks automatically generalize across different samplings and resolutions of a surface—a basic property which is crucial for practical applications. Our networks can be discretized on various geometric representations such as triangle meshes or point clouds, and can even be trained on one representation then applied to another. We optimize the spatial support of diffusion as a continuous network parameter ranging from purely local to totally global, removing the burden of manually choosing neighborhood sizes. The only other ingredients in the method are a multi-layer perceptron applied independently at each point, and spatial gradient features to support directional filters. The resulting networks are simple, robust, and efficient. Here, we focus primarily on triangle mesh surfaces, and demonstrate state-of-the-art results for a variety of tasks including surface classification, segmentation, and non-rigid correspondence.
PDF
Project
BibTeX
@article{Sharp:2022:DND,
author = {Sharp, Nicholas and Attaiki, Souhaib and Crane, Keenan and Ovsjanikov, Maks},
title = {DiffusionNet: Discretization Agnostic Learning on Surfaces},
journal = {ACM Trans. Graph.},
volume = {XX},
number = {X},
year = {2022},
publisher = {ACM},
address = {New York, NY, USA},
}
Integer Coordinates for Intrinsic Geometry Processing
 Gillespie,
Sharp,
Crane
Gillespie,
Sharp,
Crane
ACM Trans. on Graph. (2021)
Abstract
This paper describes a numerically robust data structure for encoding triangulations of polyhedral surfaces. Existing data structures either rely on floating point values to encode connectivity, or do not support remeshing operations beyond basic edge flips. We instead provide an integer-based data structure that guarantees valid connectivity, even for meshes with near-degenerate elements. Our starting point is the framework of normal coordinates from geometric topology, which we extend to the broader set of operations needed for mesh processing (vertex insertion, edge splits, etc.). The resulting data structure can be used as a drop-in replacement for earlier schemes, automatically improving reliability across a wide variety of applications. As a stress test, we successfully compute an intrinsic Delaunay refinement and associated subdivision for all manifold meshes in the Thingi10k dataset. In turn, we can compute reliable and highly accurate solutions to partial differential equations even on extremely low-quality meshes.
PDF
Project
BibTeX
@article{Gillespie:2021:ICI,
author = {Gillespie, Mark and Sharp, Nicholas and Crane, Keenan},
title = {Integer Coordinates for Intrinsic Geometry Processing},
journal = {ACM Trans. Graph.},
volume = {40},
number = {6},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
Repulsive Surfaces
 Yu,
Brakensiek,
Schumacher,
Crane
Yu,
Brakensiek,
Schumacher,
Crane
ACM Trans. on Graph. (2021)
Abstract
Functionals that penalize bending or stretching of a surface play a key role in geometric and scientific computing, but to date have ignored a very basic requirement: in many situations, surfaces must not pass through themselves or each other. This paper develops a numerical framework for optimization of surface geometry while avoiding (self-)collision. The starting point is the tangent-point energy, which effectively pushes apart pairs of points that are close in space but distant along the surface. We develop a discretization of this energy for triangle meshes, and introduce a novel acceleration scheme based on a fractional Sobolev inner product. In contrast to similar schemes developed for curves, we avoid the complexity of building a multiresolution mesh hierarchy by decomposing our preconditioner into two ordinary Poisson equations, plus forward application of a fractional differential operator. We further accelerate this scheme via hierarchical approximation, and describe how to incorporate a variety of constraints (on area, volume, etc.). Finally, we explore how this machinery might be applied to problems in mathematical visualization, geometric modeling, and geometry processing.
PDF
Project
BibTeX
@article{Yu:2021:RS,
author = {Yu, Chris and Brakensiek, Caleb and Schumacher, Henrik and Crane, Keenan},
title = {Repulsive Surfaces},
journal = {ACM Trans. Graph.},
volume = {40},
number = {6},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
Discrete Conformal Equivalence
of Polyhedral Surfaces
 Gillespie,
Springborn,
Crane
Gillespie,
Springborn,
Crane
ACM Trans. on Graph. (2021)
Abstract
This paper describes a numerical method for surface parameterization, yielding maps that are locally injective and discretely conformal in an exact sense. Unlike previous methods for discrete conformal parameterization, the method is guaranteed to work for any manifold triangle mesh, with no restrictions on triangulation quality or cone singularities. In particular we consider maps from surfaces of any genus (with or without boundary) to the plane, or globally bijective maps from genus zero surfaces to the sphere. Recent theoretical developments show that each task can be formulated as a convex problem where the triangulation is allowed to change—we complete the picture by introducing the machinery needed to actually construct a discrete conformal map. In particular, we introduce a new scheme for tracking correspondence between triangulations based on normal coordinates, and a new interpolation procedure based on layout in the light cone. Stress tests involving difficult cone configurations and near-degenerate triangulations indicate that the method is extremely robust in practice, and provides high-quality interpolation even on meshes with poor elements.
PDF
Project
BibTeX
@article{Gillespie:2021:DCE,
author = {Gillespie, Mark and Springborn, Boris and Crane, Keenan},
title = {Discrete Conformal Equivalence of Polyhedral Surfaces},
journal = {ACM Trans. Graph.},
volume = {40},
number = {4},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
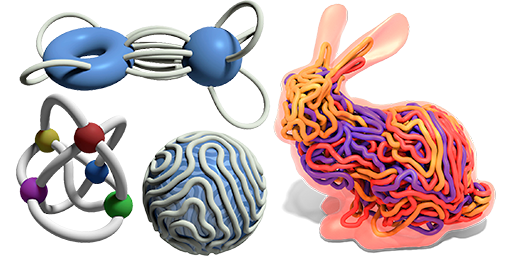
Repulsive Curves
 Yu,
Schumacher,
Crane
Yu,
Schumacher,
Crane
ACM Trans. on Graph. (2021)
Abstract
Curves play a fundamental role across computer graphics, physical simulation, and mathematical visualization, yet most tools for curve design do nothing to prevent crossings or self-intersections. This paper develops efficient algorithms for (self-)repulsion of plane and space curves that are well-suited to problems in computational design. Our starting point is the so-called tangent-point energy, which provides an infinite barrier to self-intersection. In contrast to local collision detection strategies used in, e.g., physical simulation, this energy considers interactions between all pairs of points, and is hence useful for global shape optimization: local minima tend to be aesthetically pleasing, physically valid, and nicely distributed in space. A reformulation of gradient descent, based on a Sobolev-Slobodeckij inner product enables us to make rapid progress toward local minima—independent of curve resolution. We also develop a hierarchical multigrid scheme that significantly reduces the per-step cost of optimization. The energy is easily integrated with a variety of constraints and penalties (e.g., inextensibility, or obstacle avoidance), which we use for applications including curve packing, knot untangling, graph embedding, non-crossing spline interpolation, flow visualization, and robotic path planning.
PDF
Project
BibTeX
@article{Yu:2021:RC,
author = {Yu, Chris and Schumacher, Henrik and Crane, Keenan},
title = {Repulsive Curves},
journal = {ACM Trans. Graph.},
volume = {40},
number = {2},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
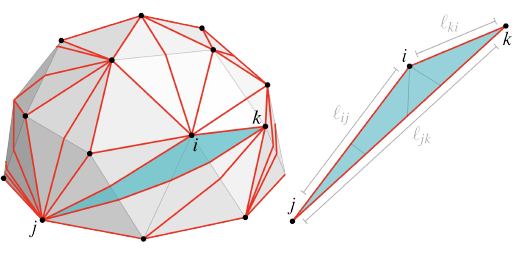
Geometry Processing with
Intrinsic Triangulations
 Sharp,
Gillespie,
Crane
Sharp,
Gillespie,
Crane
ACM SIGGRAPH Courses (2021)
Abstract
This 3-hour course provides a first introduction to intrinsic triangulations and their use in mesh processing algorithms. As geometric data becomes more ubiquitous, e.g., in applications such as augmented reality or machine learning, there is a pressing need to develop algorithms that work reliably on low-quality data. Intrinsic triangulations provide a powerful framework for these problems, by de-coupling the mesh used to encode geometry from the one used for computation. The basic shift in perspective is to encode the geometry of a mesh not in terms of ordinary vertex positions, but instead only in terms of edge lengths. Intrinsic triangulations have a long history in mathematics, but only in recent years have been applied to practical geometric computing. The course begins by giving motivation for intrinsic triangulations in terms of recent problems in computer graphics, followed by an interactive coding session where participants can make first contact with the idea of intrinsic meshes. We then give some mathematical background, and describe key data structures (overlay, signpost, normal coordinates). Using this machinery, we translate algorithms from computational geometry and scientific computing into cutting-edge algorithms for curved surfaces. For instance, we look at mesh parameterization, vector field processing, finding geodesics, solving partial differential equations (PDEs), and more. We also discuss processing of nonmanifold meshes and point clouds; participants can explore these algorithms via interactive demos. We conclude with a discussion of open questions and opportunities for future work.
PDF
Video
BibTeX
@article{Sharp:2021:GPI,
author = {Sharp, Nicholas and Gillespie, Mark and Crane, Keenan},
title = {Geometry Processing with Intrinsic Triangulations},
booktitle = {ACM SIGGRAPH 2021 courses},
series = {SIGGRAPH '21},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
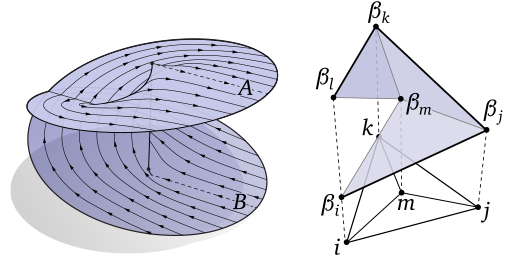
An Excursion Through
Discrete Differential Geometry
 Crane (ed.)
Crane (ed.)
Symp. App. Math. (2020)
Abstract
Discrete Differential Geometry (DDG) is an emerging discipline at the boundary between mathematics and computer science. It aims to translate concepts from classical differential geometry into a language that is purely finite and discrete, and can hence be used by algorithms to reason about geometric data. In contrast to standard numerical approximation, the central philosophy of DDG is to faithfully and exactly preserve key invariants of geometric objects at the discrete level. This process of translation from smooth to discrete helps to both illuminate the fundamental meaning behind geometric ideas and provide useful algorithmic guarantees. This volume illustrates the principles of DDG via several recent topics: discrete nets, discrete differential operators, discrete mappings, discrete conformal geometry, and discrete optimal transport.
PDF
Project
BibTeX
@book{Crane:2020:ETD,
editor = {Keenan Crane},
title = {An Excursion Through Discrete Differential Geometry},
journal = {Proceedings of Symposia in Applied Mathematics},
volume = {76},
year = {2020},
publisher = {American Mathematical Society}
}
You Can Find Geodesic
Paths in Triangle Meshes
by Just Flipping Edges
 Sharp,
Crane
Sharp,
Crane
ACM Trans. on Graph. (2020)
Abstract
This paper introduces a new approach to computing geodesics on polyhedral surfaces—the basic idea is to iteratively perform edge flips, in the same spirit as the classic Delaunay flip algorithm. This process also produces a triangulation conforming to the output geodesics, which is immediately useful for tasks in geometry processing and numerical simulation. More precisely, our FlipOut algorithm transforms a given sequence of edges into a locally shortest geodesic while avoiding self-crossings (formally: it finds a geodesic in the same isotopy class). The algorithm is guaranteed to terminate in a finite number of operations; practical runtimes are on the order of a few milliseconds, even for meshes with millions of triangles. The same approach is easily applied to curves beyond simple paths, including closed loops, curve networks, and multiply-covered curves. We explore how the method facilitates tasks such as straightening cuts and segmentation boundaries, computing geodesic Bézier curves, extending the notion of constrained Delaunay triangulations (CDT) to curved surfaces, and providing accurate boundary conditions for partial differential equations (PDEs). Evaluation on challenging datasets such as Thingi10k indicates that the method is both robust and efficient, even for low-quality triangulations.
PDF
Project
BibTeX
@article{Sharp:2020:YCF,
author = {Sharp, Nicholas and Crane, Keenan},
title = {You Can Find Geodesic Paths in Triangle Meshes by Just Flipping Edges},
journal = {ACM Trans. Graph.},
volume = {39},
number = {6},
year = {2020},
publisher = {ACM},
address = {New York, NY, USA},
}
A Laplacian for
Nonmanifold Triangle Meshes
 Sharp,
Crane
Sharp,
Crane
Symp. on Geom. Proc. (2020)
Abstract
We describe a discrete Laplacian suitable for any triangle mesh, including those that are nonmanifold or nonorientable (with or without boundary). Our Laplacian is a robust drop-in replacement for the usual cotan matrix, and is guaranteed to have nonnegative edge weights on both interior and boundary edges, even for extremely poor-quality meshes. The key idea is to build what we call a “tufted cover” over the input domain, which has nonmanifold vertices but manifold edges. Since all edges are manifold, we can flip to an intrinsic Delaunay triangulation; our Laplacian is then the cotan Laplacian of this new triangulation. This construction also provides a high-quality point cloud Laplacian, via a nonmanifold triangulation of the point set. We validate our Laplacian on a variety of challenging examples (including all models from Thingi10k), and a variety of standard tasks including geodesic distance computation, surface deformation, parameterization, and computing minimal surfaces.
PDF
Project
BibTeX
@article{Sharp:2020:LNT,
author={Nicholas Sharp and Keenan Crane},
title={{A Laplacian for Nonmanifold Triangle Meshes}},
journal={Computer Graphics Forum (SGP)},
volume={39},
number={5},
year={2020}
}
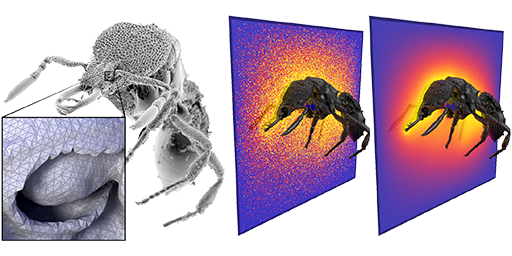
Monte Carlo
Geometry Processing
 Sawhney,
Crane
Sawhney,
Crane
ACM Trans. on Graph. (2020)
Abstract
This paper explores how core problems in PDE-based geometry processing can be efficiently and reliably solved via grid-free Monte Carlo methods. Modern geometric algorithms often need to solve Poisson-like equations on geometrically intricate domains. Conventional methods most often mesh the domain, which is both challenging and expensive for geometry with fine details or imperfections (holes, self-intersections, etc.). In contrast, grid-free Monte Carlo methods avoid mesh generation entirely, and instead just evaluate closest point queries. They hence do not discretize space, time, nor even function spaces, and provide the exact solution (in expectation) even on extremely challenging models. More broadly, they share many benefits with Monte Carlo methods from photorealistic rendering: excellent scaling, trivial parallel implementation, view-dependent evaluation, and the ability to work with any kind of geometry (including implicit or procedural descriptions). We develop a complete “black box” solver that encompasses integration, variance reduction, and visualization, and explore how it can be used for various geometry processing tasks. In particular, we consider several fundamental linear elliptic PDEs with constant coefficients on solid regions of Rn. Overall we find that Monte Carlo methods significantly broaden the horizons of geometry processing, since they easily handle problems of size and complexity that are essentially hopeless for conventional methods.
Project
PDF
BibTeX
@article{Sawhney:2020:MCG,
author = {Sawhney, Rohan and Crane, Keenan},
title = {Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains},
journal = {ACM Trans. Graph.},
volume = {39},
number = {4},
year = {2020},
publisher = {ACM},
address = {New York, NY, USA},
}
Penrose: From Mathematical Notation to Beautiful Diagrams
 Ye,
Ni,
Krieger,
Ma'ayan,
Wise,
Ye,
Ni,
Krieger,
Ma'ayan,
Wise,
Aldrich,
Sunshine,
Crane
ACM Trans. on Graph. (2020)
Abstract
We introduce a system called Penrose for creating mathematical diagrams. Its basic functionality is to translate abstract statements written in familiar math-like notation into one or more possible visual representations. Rather than rely on a fixed library of visualization tools, the visual representation is user-defined in a constraint-based specification language; diagrams are then generated automatically via constrained numerical optimization. The system is user-extensible to many domains of mathematics, and is fast enough for iterative design exploration. In contrast to tools that specify diagrams via direct manipulation or low-level graphics programming, Penrose enables rapid creation and exploration of diagrams that faithfully preserve the underlying mathematical meaning. We demonstrate the effectiveness and generality of the system by showing how it can be used to illustrate a diverse set of concepts from mathematics and computer graphics.
Project
PDF
BibTeX
@article{Ye:2020:PFM,
author = {Ye, Katherine and Ni, Wode and Krieger, Max and Ma'ayan, Dor and Wise, Jenna and Aldrich, Jonathan and Sunshine, Joshua and Crane, Keenan},
title = {Penrose: From Mathematical Notation to Beautiful Diagrams},
journal = {ACM Trans. Graph.},
volume = {39},
number = {4},
year = {2020},
publisher = {ACM},
address = {New York, NY, USA},
}
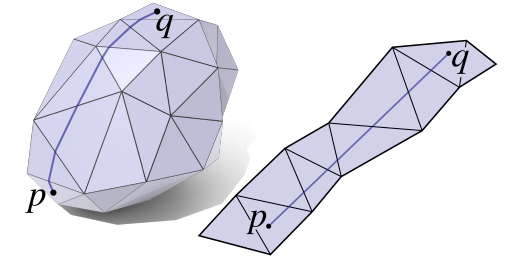
A Survey of Algorithms
for Geodesic Paths
and Distances
 Crane,
Marco Livesu,
Puppo,
Qin
Crane,
Marco Livesu,
Puppo,
Qin
arXiv preprint (2020)
Abstract
Numerical computation of shortest paths or geodesics on curved domains, as well as the associated geodesic distance, arises in a broad range of applications across digital geometry processing, scientific computing, computer graphics, and computer vision. Relative to Euclidean distance computation, these tasks are complicated by the influence of curvature on the behavior of shortest paths, as well as the fact that the representation of the domain may itself be approximate. In spite of the difficulty of this problem, recent literature has developed a wide variety of sophisticated methods that enable rapid queries of geodesic information, even on relatively large models. This survey reviews the major categories of approaches to the computation of geodesic paths and distances, highlighting common themes and opportunities for future improvement.
BibTeX
@article{Crane:2020:SAG,
author = {{Crane}, Keenan and {Livesu}, Marco and {Puppo}, Enrico and {Qin}, Yipeng},
title = "{A Survey of Algorithms for Geodesic Paths and Distances}",
journal = {arXiv e-prints},
keywords = {Computer Science - Graphics, Computer Science - Computational Geometry},
year = 2020,
month = jul,
eid = {arXiv:2007.10430},
pages = {arXiv:2007.10430},
archivePrefix = {arXiv},
eprint = {2007.10430},
primaryClass = {cs.GR},
}
Navigating Intrinsic Triangulations
 Sharp,
Soliman,
Crane
Sharp,
Soliman,
Crane
ACM Trans. on Graph. (2019)
Abstract
We present a data structure that makes it easy to run a large class of algorithms from computational geometry and scientific computing on extremely poor-quality surface meshes. Rather than changing the geometry, as in traditional remeshing, we consider intrinsic triangulations which connect vertices by straight paths along the exact geometry of the input mesh. Our key insight is that such a triangulation can be encoded implicitly by storing the direction and distance to neighboring vertices. The resulting signpost data structure then allows geometric and topological queries to be made on-demand by tracing paths across the surface. Existing algorithms can be easily translated into the intrinsic setting, since this data structure supports the same basic operations as an ordinary triangle mesh (vertex insertions, edge splits, etc.). The output of intrinsic algorithms can then be stored on an ordinary mesh for subsequent use; unlike previous data structures, we use a constant amount of memory and do not need to explicitly construct an overlay mesh unless it is specifically requested. Working in the intrinsic setting incurs little computational overhead, yet we can run algorithms on extremely degenerate inputs, including all manifold meshes from the Thingi10k data set. To evaluate our data structure we implement several fundamental geometric algorithms including intrinsic versions of Delaunay refinement and optimal Delaunay triangulation, approximation of Steiner trees, adaptive mesh refinement for PDEs, and computation of Poisson equations, geodesic distance, and flip-free tangent vector fields.
Project
PDF
BibTeX
@article{Sharp:2019:NIT,
author = {Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
title = {Navigating Intrinsic Triangulations},
journal = {ACM Trans. Graph.},
volume = {38},
number = {4},
year = {2019},
publisher = {ACM},
address = {New York, NY, USA},
}
Symmetric Moving Frames
 Corman,
Crane
Corman,
Crane
ACM Trans. on Graph. (2019)
Abstract
A basic challenge in field-guided hexahedral meshing is to find a spatially-varying frame that is adapted to the domain geometry and is continuous up to symmetries of the cube. We introduce a fundamentally new representation of such 3D cross fields based on Cartan's method of moving frames. Our key observation is that cross fields and ordinary frame fields are locally characterized by identical conditions on their Darboux derivative. Hence, by using derivatives as the principal representation (and only later recovering the field itself), one avoids the need to explicitly account for symmetry during optimization. At the discrete level, derivatives are encoded by skew-symmetric matrices associated with the edges of a tetrahedral mesh; these matrices encode arbitrarily large rotations along each edge, and can robustly capture singular behavior even on coarse meshes. We apply this representation to compute 3D cross fields that are as smooth as possible everywhere but on a prescribed network of singular curves—since these fields are adapted to curve tangents, they can be directly used as input for field-guided mesh generation algorithms. Optimization amounts to an easy nonlinear least squares problem that behaves like a convex program in the sense that it always appears to produce the same result, independent of initialization. We study the numerical behavior of this procedure, and perform some preliminary experiments with mesh generation.
PDF
Project
BibTeX
@article{Corman:2019:SMF,
author = {Corman, Etienne and Crane, Keenan},
title = {Symmetric Moving Frames},
journal = {ACM Trans. Graph.},
volume = {38},
number = {4},
year = {2019},
publisher = {ACM},
address = {New York, NY, USA},
}
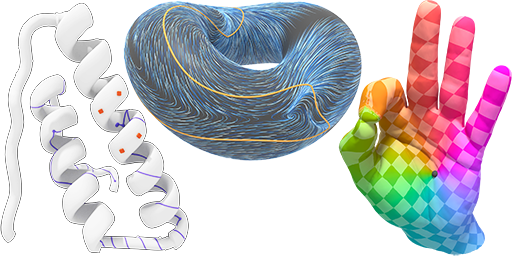
The Vector Heat Method
 Sharp,
Soliman,
Crane
Sharp,
Soliman,
Crane
ACM Trans. on Graph. (2019)
Abstract
This paper describes a method for efficiently computing parallel transport of tangent vectors on curved surfaces, or more generally, any vector-valued data on a curved manifold. More precisely, it extends a vector field defined over any region to the rest of the domain via parallel transport along shortest geodesics. This basic operation enables fast, robust algorithms for extrapolating level set velocities, inverting the exponential map, computing geometric medians and Karcher/Fréchet means of arbitrary distributions, constructing centroidal Voronoi diagrams, and finding consistently ordered landmarks. Rather than evaluate parallel transport by explicitly tracing geodesics, we show that it can be computed via a short-time heat flow involving the connection Laplacian. As a result, transport can be achieved by solving three prefactored linear systems, each akin to a standard Poisson problem. To implement the method we need only a discrete connection Laplacian, which we describe for a variety of geometric data structures (point clouds, polygon meshes, \etc). We also study the numerical behavior of our method, showing empirically that it converges under refinement, and augment the construction of intrinsic Delaunay triangulations (iDT) so that they can be used in the context of tangent vector field processing.
PDF
Project
BibTeX
@article{Sharp:2019:VHM,
author = {Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
title = {The Vector Heat Method},
journal = {ACM Trans. Graph.},
volume = {38},
number = {3},
year = {2019},
publisher = {ACM},
address = {New York, NY, USA},
}
Conformal Geometry of
Simplicial Surfaces

Crane
Proceedings of Symposia in
Applied Mathematics
Abstract
Conformal geometry studies geometric properties that are invariant with respect to angle-preserving transformations. In the discrete setting of polyhedral surfaces, the idea of naively preserving angles leads to a notion of conformal geometry that is far too rigid, i.e., it does not capture the rich behavior found in the smooth setting. These notes explore several alternative notions of discrete conformal structure, culminating with a recent uniformization theorem for general simplicial surfaces. Topics covered include circle packings, circle patterns, inversive distance, discrete Yamabe flow, and connections to variational principles for ideal hyperbolic polyhedra. (This chapter is an extended version of course notes developed for the 2018 AMS Short Course on Discrete Differential Geometry.)
Project
BibTeX
@incollection{Crane:2020:DCG,
author = "Keenan Crane",
title = {{Conformal Geometry of Simplicial Surfaces}},
booktitle = "Proceedings of Symposia in Applied Mathematics",
publisher = "American Mathematical Society",
year = 2020,
}
Developability of Triangle Meshes
 Stein,
Grinspun,
Crane
Stein,
Grinspun,
Crane
ACM Trans. on Graph. (2018)
Abstract
Developable surfaces are those that can be made by smoothly bending flat pieces without stretching or shearing. We introduce a definition of developability for triangle meshes which exactly captures two key properties of smooth developable surfaces, namely flattenability and presence of straight ruling lines. This definition provides a starting point for algorithms in developable surface modeling—we consider a variational approach that drives a given mesh toward developable pieces separated by regular seam curves. Computation amounts to gradient descent on an energy with support in the vertex star, without the need to explicitly cluster patches or identify seams. We briefly explore applications to developable design and manufacturing.
BibTeX
@article{Stein:2018:DSF,
author = {Stein, Oded and Grinspun, Eitan and Crane, Keenan},
title = {Developability of Triangle Meshes},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
Variational Surface Cutting
 Sharp,
Crane
Sharp,
Crane
ACM Trans. on Graph. (2018)
Abstract
This paper develops a global variational approach to cutting curved surfaces so that they can be flattened into the plane with low metric distortion. Such cuts are a critical component in a variety of algorithms that seek to parameterize surfaces over flat domains, or fabricate structures from flat materials. Rather than evaluate the quality of a cut solely based on properties of the curve itself (e.g., its length or curvature), we formulate a flow that directly optimizes the distortion induced by cutting and flattening. Notably, we do not have to explicitly parameterize the surface in order to evaluate the cost of a cut, but can instead integrate a simple evolution equation defined on the cut curve itself. We arrive at this flow via a novel application of shape derivatives to the Yamabe equation from conformal geometry. We then develop an Eulerian numerical integrator on triangulated surfaces, which does not restrict cuts to mesh edges and can incorporate user-defined data such as importance or occlusion. The resulting cut curves can be used to drive distortion to arbitrarily low levels, and have a very different character from cuts obtained via purely discrete formulations. We briefly explore potential applications to computational design, as well as connections to space filling curves and the problem of uniform heat distribution.
BibTeX
@article{Sharp:2018:VSC,
author = {Sharp, Nick and Crane, Keenan},
title = {Variational Surface Cutting},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
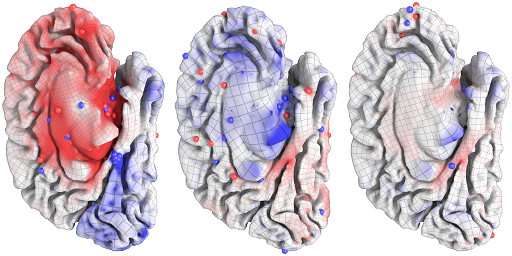
Optimal Cone Singularities
for Conformal Flattening
 Soliman,
Slepčev,
Crane
Soliman,
Slepčev,
Crane
ACM Trans. on Graph. (2018)
Abstract
Angle-preserving or conformal surface parameterization has proven to be a powerful tool across applications ranging from geometry processing, to digital manufacturing, to machine learning, yet conformal maps can still suffer from severe area distortion. Cone singularities provide a way to mitigate this distortion, but finding the best configuration of cones is notoriously difficult. This paper develops a strategy that is globally optimal in the sense that it minimizes total area distortion among all possible cone configurations (number, placement, and size) that have no more than a fixed total cone angle. A key insight is that, for the purpose of optimization, one should not work directly with curvature measures (which naturally represent cone configurations), but can instead apply Fenchel-Rockafellar duality to obtain a formulation involving only ordinary functions. The result is a convex optimization problem, which can be solved via a sequence of sparse linear systems easily built from the usual cotangent Laplacian. The method supports user-defined notions of importance, constraints on cone angles (e.g., positive, or within a given range), and sophisticated boundary conditions (e.g., convex, or polygonal). We compare our approach to previous techniques on a variety of challenging models, often achieving dramatically lower distortion, and demonstrating that global optimality leads to extreme robustness in the presence of noise or poor discretization.
BibTeX
@article{Soliman:2018:OCS,
author = {Soliman, Yousuf and Slep\v{c}ev, Dejan and Crane, Keenan},
title = {Optimal Cone Singularities for Conformal Flattening},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
Rapid Deployment of
Curved Surfaces via
Programmable Auxetics
 Konaković,
Panetta,
Crane,
Pauly
Konaković,
Panetta,
Crane,
Pauly
ACM Trans. on Graph. (2018)
Abstract
Deployable structures are physical mechanisms that can easily transition between two or more geometric configurations; such structures enable industrial, scientific, and consumer applications at a wide variety of scales. This paper develops novel deployable structures that can approximate a large class of doubly-curved surfaces and are easily actuated from a flat initial state via inflation or gravitational loading. The structures are based on two-dimensional rigid mechanical linkages that implicitly encode the curvature of the target shape via a user-programmable pattern that permits locally isotropic scaling under load. We explicitly characterize the shapes that can be realized by such structures—in particular, we show that they can approximate target surfaces of positive mean curvature and bounded scale distortion relative to a given reference domain. Based on this observation, we develop efficient computational design algorithms for approximating a given input geometry. The resulting designs can be rapidly manufactured via digital fabrication technologies such as laser cutting, CNC milling, or 3D printing. We validate our approach through a series of physical prototypes and present several application case studies, ranging from surgical implants to large-scale deployable architecture.
PDF
Project
BibTeX
@article{Konakovic:2018:RDC,
author = {Konakovi\'{c}, Mina and Panetta, Julian and Crane, Keenan and Pauly, Mark},
title = {Rapid Deployment of Curved Surfaces via Programmable Auxetics},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
Möbius Registration
 Baden,
Crane,
Kazhdan
Baden,
Crane,
Kazhdan
Symp. on Geom. Proc. (2018)
Abstract
Conformal parameterizations over the sphere provide high-quality maps between genus zero surfaces, and are essential for applications such as data transfer and comparative shape analysis. However, such maps are not unique: to define correspondence between two surfaces, one must find the Möbius transformation that best aligns two parameterizations—akin to picking a translation and rotation in rigid registration problems. We describe a simple procedure that canonically centers and rotationally aligns two spherical maps. Centering is implemented via elementary operations on triangle meshes in R3, and minimizes area distortion. Alignment is achieved using the FFT over the group of rotations. We examine this procedure in the context of spherical conformal parameterization, orbifold maps, non-rigid symmetry detection, and dense point-to-point surface correspondence.
PDF
Project
BibTeX
@article{Baden:2018:MR,
author={Alex Baden and Keenan Crane and Misha Kazhdan},
title={{M\"{o}bius Registration}},
journal={Computer Graphics Forum (SGP)},
volume={37},
number={5},
year={2018}
}
Boundary First Flattening

ACM Trans. on Graph. (2017)
Abstract
A conformal flattening maps a curved surface to the plane without distorting angles—such maps have become a fundamental building block for problems in geometry processing, numerical simulation, and computational design. Yet existing methods provide little direct control over the shape of the flattened domain, or else demand expensive nonlinear optimization. Boundary first flattening (BFF) is a linear method for conformal parameterization which is faster than traditional linear methods, yet provides control and quality comparable to sophisticated nonlinear schemes. The key insight is that the boundary data for many conformal mapping problems can be efficiently constructed via the Cherrier formula together with a pair of Poincaré-Steklov operators; once the boundary is known, the map can be easily extended over the rest of the domain. Since computation demands only a single factorization of the real Laplace matrix, the amortized cost is about 50x less than any previously published technique for boundary-controlled conformal flattening. As a result, BFF opens the door to real-time editing or fast optimization of high-resolution maps, with direct control over boundary length or angle. We show how this method can be used to construct maps with sharp corners, cone singularities, minimal area distortion, and uniformization over the unit disk; we also demonstrate for the first time how a surface can be conformally flattened directly onto any given target shape.
PDF
Project
BibTeX
@article{Sawhney:2017:BFF,
author = {Sawhney, Rohan and Crane, Keenan},
title = {Boundary First Flattening},
journal = {ACM Trans. Graph.},
volume = {37},
number = {1},
month = dec,
year = {2017},
issn = {0730-0301},
pages = {5:1--5:14},
articleno = {5},
numpages = {14},
url = {http://doi.acm.org/10.1145/3132705},
doi = {10.1145/3132705},
acmid = {3132705},
publisher = {ACM},
address = {New York, NY, USA}
}
The Heat Method
for Distance Computation

Communications of the ACM (2017)
Abstract
We introduce the heat method for solving the single- or multiple-source shortest path problem on both flat and curved domains. A key insight is that distance computation can be split into two stages: first find the direction along which distance is increasing, then compute the distance itself. The heat method is robust, efficient, and simple to implement since it is based on solving a pair of standard sparse linear systems. These systems can be factored once and subsequently solved in near-linear time, substantially reducing amortized cost. Real-world performance is an order of magnitude faster than state-of-the-art methods, while maintaining a comparable level of accuracy. The method can be applied in any dimension, and on any domain that admits a gradient and inner product—including regular grids, triangle meshes, and point clouds. Numerical evidence indicates that the method converges to the exact distance in the limit of refinement; we also explore smoothed approximations of distance suitable for applications where greater regularity is desired.
Project
BibTeX
@article{Crane:2017:HMD,
author = {Crane, Keenan and Weischedel, Clarisse and Wardetzky, Max},
title = {The Heat Method for Distance Computation},
journal = {Commun. ACM},
issue_date = {November 2017},
volume = {60},
number = {11},
month = oct,
year = {2017},
issn = {0001-0782},
pages = {90--99},
numpages = {10},
url = {http://doi.acm.org/10.1145/3131280},
doi = {10.1145/3131280},
acmid = {3131280},
publisher = {ACM},
address = {New York, NY, USA},
}
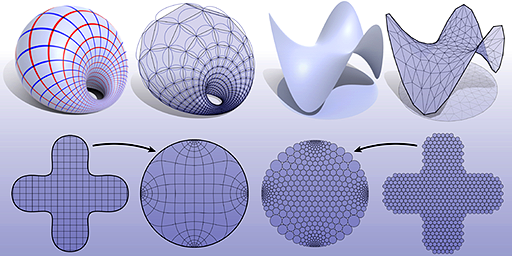
A Glimpse Into
Discrete Differential Geometry
Notices of the American Mathematical
Society (2017)
Abstract
The emerging field of discrete differential geometry (DDG) studies discrete analogues of smooth geometric objects, providing an essential link between analytical descriptions and computation. In recent years it has unearthed a rich variety of new perspectives on applied problems in computational anatomy/biology, computational mechanics, industrial design, computational architecture, and digital geometry processing at large. The basic philosophy of discrete differential geometry is that a discrete object like a polyhedron is not merely an approximation of a smooth one, but rather a differential geometric object in its own right. In contrast to traditional numerical analysis which focuses on eliminating approximation error in the limit of refinement (e.g., by taking smaller and smaller finite differences), DDG places an emphasis on the so-called “mimetic” viewpoint, where key properties of a system are preserved exactly, independent of how large or small the elements of a mesh might be. Just as algorithms for simulating mechanical systems might seek to exactly preserve physical invariants such as total energy or momentum, structure-preserving models of discrete geometry seek to exactly preserve global geometric invariants such as total curvature. More broadly, DDG focuses on the discretization of objects that do not naturally fall under the umbrella of traditional numerical analysis. This article provides an overview of some of the themes in DDG.
PDF
BibTeX
@article{Crane:2017:GID,
author={Keenan Crane and Max Wardetzky},
title={A Glimpse Into Discrete Differential Geometry},
journal={Notices of the American Mathematical Society},
month={November},
volume={64},
number={10},
pages={1153--1159},
year={2017}
}
SUBSTANCE and STYLE:
Domain-Specific Languages
for Mathematical Diagrams
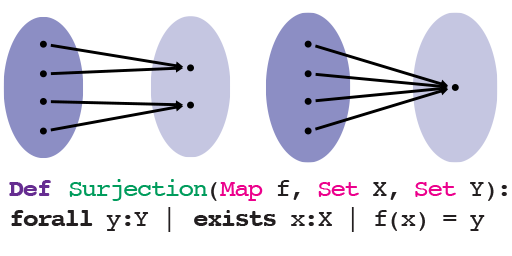
DSLDI (2017)
Abstract
Creating mathematical diagrams is essential for both developing one’s intuition and conveying it to others. However, formalizing diagrams in most general-purpose tools requires painstaking low-level manipulation of shapes and positions. We report on early work on PENROSE, a system we are building to automatically visualize mathematics from notation. PENROSE comprises two languages: SUBSTANCE, a domain-specific language that mimics the declarativeness of mathematical notation, and STYLE, a styling language that concisely specifies the visual semantics of the notation. Our system can automatically visualize set theory expressions with user-defined styles, and it can visualize abstract definitions of functions by producing concrete examples. We plan to extend the system to more domains of math.
PDF
BibTeX
@inproceedings{Ni:2017:SSD,
author={Wode Ni and Katherine Ye and Joshua Sunshine and Jonathan Aldrich and Keenan Crane},
title={SUBSTANCE and STYLE: domain-specific languages for mathematical diagrams},
booktitle={DSLDI (Domain-Specific Language Design and Implementation)},
year={2017}
}
A Dirac Operator for
Extrinsic Shape Analysis

Symp. on Geom. Proc. (2017)
Abstract
The eigenfunctions and eigenvalues of the Laplace-Beltrami operator have proven to be a powerful tool for digital geometry processing, providing a description of geometry that is essentially independent of coordinates or the choice of discretization. However, since Laplace-Beltrami is purely intrinsic it struggles to capture important phenomena such as extrinsic bending, sharp edges, and fine surface texture. We introduce a new extrinsic differential operator called the relative Dirac operator, leading to a family of operators with a continuous trade-off between intrinsic and extrinsic features. Previous operators are either fully or partially intrinsic. In contrast, the proposed family spans the entire spectrum: from completely intrinsic (depending only on the metric) to completely extrinsic (depending only on the Gauss map). By adding an infinite potential well to this (or any) operator we can also robustly handle surface patches with irregular boundary. We explore use of these operators for a variety of shape analysis tasks, and study their performance relative to operators previously found in the geometry processing literature.
PDF
Project
BibTeX
@article{Liu:2017:DOE,
author={Derek Liu and Alec Jacobson and Keenan Crane},
title={A Dirac Operator for Extrinsic Shape Analysis},
journal={Computer Graphics Forum (SGP)},
volume={36},
number={5},
year={2017}
}
Designing Extensible, Domain-Specific Languages for Mathematical Diagrams
OBT (2017)
Abstract
In science, a well-chosen illustration can turn bafflement into enlightenment. Yet technical exposition remains largely textual, due to the tremendous expertise required to produce high-quality figures. We propose PENROSE, a system to automatically generate professional-quality mathematical illustrations from high-level, purely semantic descriptions of mathematical objects. Unlike low-level tools where diagrams are specified via graphical primitives, a mathematically-inclined user should not require any graphic design skill to create beautiful diagrams. PENROSE comprises two extensible domain-specific languages (DSLs): SUBSTANCE, which diagrammers use to specify mathematical objects and relationships, and STYLE, which implementers use to encode various ways of realizing these relationships visually, akin to the separation of content and style in modern HTML/CSS. To compile diagrams, we are developing a sophisticated constraint solver incorporating techniques from optimization and computer graphics.
PDF
BibTeX
@inproceedings{Ye:2017:DED,
author={Katherine Ye and Keenan Crane and Joshua Sunshine and Jonathan Aldrich},
title={Designing Extensible, Domain-Specific Languages for Mathematical Diagrams},
booktitle={OBT (Off the Beaten Track)},
year={2017}
}
Computational Design of
Telescoping Structures

ACM Trans. on Graph. (2017)
Abstract
Telescoping structures are valuable for a variety of applications where mechanisms must be compact in size and yet easily deployed. So far, however, there has been no systematic study of the types of shapes that can be modeled by telescoping structures, nor practical tools for telescopic design. We present a novel geometric characterization of telescoping curves, and explore how free-form surfaces can be approximated by networks of such curves. In particular we consider piecewise helical space curves with torsional impulses, which significantly generalize the linear telescopes found in typical engineering designs. Based on this principle we develop a system for computational design and fabrication which allows users to explore the space of telescoping structures; inputs to our system include user sketches or arbitrary meshes, which are then converted to a curve skeleton. We prototype applications in animation, fabrication, and robotics, using our system to design a variety of both simulated and fabricated examples.
PDF
BibTeX
@article{Yu:2017:CDT,
author = {Yu, Chris and Crane, Keenan and Coros, Stelian},
title = {Computational Design of Telescoping Structures},
journal = {ACM Trans. Graph.},
volume = {36},
number = {4},
year = {2017},
publisher = {ACM},
address = {New York, NY, USA},
}
Beyond Developable: Computational Design and Fabrication with Auxetic Materials
 Konaković,
Crane,
Deng,
Konaković,
Crane,
Deng,
Bouaziz,
Piker,
Pauly
ACM Trans. on Graph. (2016)
Abstract
We present a computational method for interactive 3D design and rationalization of surfaces via auxetic materials, i.e., flat flexible material that can stretch uniformly up to a certain extent. A key motivation for studying such material is that one can approximate doubly-curved surfaces (such as the sphere) using only flat pieces, making it attractive for fabrication. We physically realize surfaces by introducing cuts into approximately inextensible material such as sheet metal, plastic, or leather. The cutting pattern is modeled as a regular triangular linkage that yields hexagonal openings of spatially-varying radius when stretched. In the same way that isometry is fundamental to modeling developable surfaces, we leverage conformal geometry to understand auxetic design. In particular, we compute a global conformal map with bounded scale factor to initialize an otherwise intractable nonlinear optimization. We demonstrate that this global approach can handle non-trivial topology and non-local dependencies inherent in auxetic material. Design studies and physical prototypes are used to illustrate a wide range of possible applications.
BibTeX
@article{Konakovic:2016:BDC,
author = {Konakovi\'{c}, Mina and Crane, Keenan and Deng, Bailin and Bouaziz, Sofien and Piker, Daniel and Pauly, Mark},
title = {Beyond Developable: Computational Design and Fabrication with Auxetic Materials},
journal = {ACM Trans. Graph.},
volume = {35},
number = {4},
year = {2016},
publisher = {ACM},
address = {New York, NY, USA},
}
Stripe Patterns on Surfaces
 Knöppel,
Crane,
Pinkall,
Schröder
Knöppel,
Crane,
Pinkall,
Schröder
ACM Trans. on Graph. (2015)
Abstract
Stripe patterns are ubiquitous in nature, describing macroscopic phenomena such as stripes on plants and animals, down to material impurities on the atomic scale. We propose an algorithm for synthesizing stripe patterns on triangulated surfaces, where branch points are automatically inserted in order to achieve user-specified orientation and line spacing. Patterns are characterized as global minimizers of a simple convex-quadratic energy which is well-defined in the smooth setting. Computation amounts to finding the smallest eigenvector of a symmetric positive-definite matrix with the same sparsity pattern as the standard graph Laplacian. The resulting patterns are globally continuous, and can be applied to a variety of tasks in design and texture synthesis.
BibTeX
@article{Knoppel:2015:SPS,
author = {Kn\"{o}ppel, Felix and Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Stripe Patterns on Surfaces},
journal = {ACM Trans. Graph.},
volume = {34},
number = {4},
year = {2015},
publisher = {ACM},
address = {New York, NY, USA},
}
A General Framework for
Bilateral and Mean Shift Filtering
 Solomon,
Crane,
Butscher,
Wojtan
Solomon,
Crane,
Butscher,
Wojtan
arXiv:1405.4734 (2014)
Abstract
We present a generalization of the bilateral filter that can be applied to feature-preserving smoothing of signals on images, meshes, and other domains within a single unified framework. Our discretization is competitive with state-of-the-art smoothing techniques in terms of both accuracy and speed, is easy to implement, and has parameters that are straightforward to understand. Unlike previous bilateral filters developed for meshes and other irregular domains, our construction reduces exactly to the image bilateral on rectangular domains and comes with a rigorous foundation in both the smooth and discrete settings. These guarantees allow us to construct unconditionally convergent mean-shift schemes that handle a variety of extremely noisy signals. We also apply our framework to geometric edge-preserving effects like feature enhancement and show how it is related to local histogram techniques.
BibTeX
@article{Solomon:2014:GFB,
author = {Solomon, Justin and Crane, Keenan and Butscher, Adrian and Wojtan, Chris},
title = {A General Framework for Bilateral and Mean Shift Filtering},
journal = {ArXiv e-prints},
volume = {32},
archivePrefix = "arXiv",
eprint = {1405.4734},
primaryClass = "cs.GR",
keywords = {Computer Science - Graphics},
year = {2014},
month = {April}
}
Robust Fairing via
Conformal Curvature Flow
 Crane,
Pinkall,
Schröder
Crane,
Pinkall,
Schröder
ACM Trans. on Graph. (2013)
Abstract
This paper presents a formulation of Willmore flow for triangulated surfaces that permits extraordinarily large time steps and naturally preserves the quality of the input mesh. The main insight is that Willmore flow becomes remarkably stable when expressed in curvature space—we develop the precise conditions under which curvature is allowed to evolve. The practical outcome is a highly efficient algorithm that naturally preserves texture and does not require remeshing during the flow. We apply this algorithm to surface fairing, geometric modeling, and construction of constant mean curvature (CMC) surfaces. We also present a new algorithm for length-preserving flow on planar curves, which provides a valuable analogy for the surface case.
BibTeX
@article{Crane:2013:RFC,
author = {Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Robust Fairing via Conformal Curvature Flow},
journal = {ACM Trans. Graph.},
volume = {32},
number = {4},
year = {2013},
publisher = {ACM},
address = {New York, NY, USA},
}
Globally Optimal Direction Fields
 Knöppel,
Crane,
Pinkall,
Schröder
Knöppel,
Crane,
Pinkall,
Schröder
ACM Trans. on Graph. (2013)
Abstract
This paper presents a method for constructing smooth unit n-direction fields (line fields, cross fields, etc.) on surfaces that is an order of magnitude faster than state-of-the-art methods, while still producing fields of equal or better quality. The method is based on a simple quadratic energy whose minimizers are globally optimal in the sense that they produce the smoothest fields over all possible configurations of singularities (number, location, and index). The method is fully automatic and can optionally produce fields aligned with a given guidance field, for example, principal curvature directions. Computationally the smoothest field is found via a sparse eigenvalue problem involving a matrix similar to the cotan-Laplacian. When a guidance field is present, finding the optimal field amounts to solving a single linear Poisson problem.
BibTeX
@article{Knoppel:2013:GOD,
author = {Kn\"{o}ppel, Felix and Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Globally optimal direction fields},
journal = {ACM Trans. Graph.},
volume = {32},
number = {4},
year = {2013},
publisher = {ACM},
address = {New York, NY, USA},
}
Digital Geometry Processing with
Discrete Exterior Calculus
 Crane,
de Goes,
Desbrun,
Schröder
Crane,
de Goes,
Desbrun,
Schröder
SIGGRAPH 2013 Course Notes
Abstract
This course provides an introduction to geometry processing using discrete exterior calculus (DEC). DEC provides a simple, flexible, and efficient framework within which one can build a unified platform for geometry processing. The course provides essential mathematical background as well as a large array of real-world examples. It also provides a short survey of the most relevant recent developments in digital geometry processing and discrete differential geometry.
BibTeX
@inproceedings{Crane:2013:DGP,
author = {Keenan Crane and Fernando de Goes and Mathieu Desbrun and Peter Schr\"{o}der},
title = {Digital Geometry Processing with Discrete Exterior Calculus},
booktitle = {ACM SIGGRAPH 2013 courses},
series = {SIGGRAPH '13},
year = {2013},
location = {Anaheim, California},
numpages = {126},
publisher = {ACM},
address = {New York, NY, USA},
}
Spin Transformations
of Discrete Surfaces
 Crane,
Pinkall,
Schröder
Crane,
Pinkall,
Schröder
ACM Trans. on Graph. (2011)
Abstract
This paper introduces a new method for computing conformal transformations of triangle meshes in R3. Conformal maps are desirable in digital geometry processing because they do not exhibit shear, and therefore preserve texture fidelity as well as the quality of the mesh itself. Traditional discretizations consider maps into the complex plane, which are useful only for problems such as surface parameterization and planar shape deformation where the target surface is flat. We instead consider maps into the quaternions, which allows us to work directly with surfaces sitting in R3. In particular, we introduce a quaternionic Dirac operator and use it to develop a novel integrability condition on conformal deformations. Our discretization of this condition results in a sparse linear system that is simple to build and can be used to efficiently edit surfaces by manipulating curvature and boundary data, as demonstrated via several mesh processing applications.
BibTeX
@article{Crane:2011:STD,
author = {Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Spin Transformations of Discrete Surfaces},
journal = {ACM Trans. Graph.},
volume = {30},
number = {4},
year = {2011},
publisher = {ACM},
address = {New York, NY, USA},
}
Discrete Connections
for Geometry Processing
 Keenan Crane
Keenan Crane
Caltech Master's Thesis (2010)
Abstract
Connections provide a way to compare local quantities defined at different points of a geometric space. This thesis develops a discrete theory of connections that naturally leads to practical, efficient numerical algorithms for geometry processing, including texture synthesis and quadrilateral remeshing. Our formulation is motivated by real-world applications where meshes may be noisy or coarsely discretized. Further, because our discrete framework closely parallels the smooth theory, we can draw upon a huge wealth of existing knowledge to develop and interpret mesh processing algorithms. The solutions we produce are globally optimal in the sense that they describe the trivial connection closest to Levi-Civita among all solutions with the prescribed set of singularities. Relative to previous methods our algorithm is surprisingly simple, and can be implemented using standard operations from mesh processing and linear algebra.
BibTeX
@mastersthesis{caltechthesis5880,
title = {Discrete connections for geometry processing},
school = {California Institute of Technology},
author = {Keenan Crane},
year = {2010},
url = {http://resolver.caltech.edu/CaltechTHESIS:05282010-102307125}
}
Trivial Connections
on Discrete Surfaces
 Crane,
Desbrun,
Schröder
Crane,
Desbrun,
Schröder
Symp. on Geometry Proc. (2010)
Abstract
This paper presents a straightforward algorithm for constructing connections on surfaces that are as smooth as possible everywhere but on a prescribed set of isolated singularities with given index. Such connections can be used to design rotationally symmetric direction fields, which are essential in applications such as quadrilateral remeshing and texture synthesis. We compute connections by solving a single sparse linear system built from standard operators. Our solutions are globally optimal in the sense that they describe the trivial connection closest to Levi-Civita among all connections with the prescribed set of singularities. Relative to previous methods our algorithm is surprisingly simple, and can be implemented using standard operations from mesh processing and linear algebra.
BibTeX
@article{Crane:2010:TCD,
author={Keenan Crane and Mathieu Desbrun and Peter Schr\"{o}der},
title={Trivial Connections on Discrete Surfaces},
journal={Computer Graphics Forum (SGP)},
volume={29},
number={5},
pages={1525-1533},
year={2010}
}
Lie Group Integrators for
Animation and Control of Vehicles
 Kobilarov,
Crane,
Desbrun
Kobilarov,
Crane,
Desbrun
ACM Trans. on Graph. (2009)
Abstract
This paper is concerned with the animation and control of vehicles with complex dynamics such as helicopters, boats, and cars. Motivated by recent developments in discrete geometric mechanics we develop a general framework for integrating the dynamics of holonomic and nonholonomic vehicles by preserving their state-space geometry and motion invariants. We demonstrate that the resulting integration schemes are superior to standard methods in numerical robustness and efficiency, and can be applied to many types of vehicles. In addition, we show how to use this framework in an optimal control setting to automatically compute accurate and realistic motions for arbitrary user-specified constraints.
BibTeX
@article{Kobilarov:2009:LGI,
author = {Kobilarov, Marin and Crane, Keenan and Desbrun, Mathieu},
title = {Lie group integrators for animation and control of vehicles},
journal = {ACM Trans. Graph.},
volume = {28},
number = {2},
month = {May},
year = {2009},
}
Energy-Preserving Integrators
for Fluid Animation
 Mullen,
Crane,
Pavlov,
Tong,
Desbrun
Mullen,
Crane,
Pavlov,
Tong,
Desbrun
ACM Trans. on Graph. (2009)
Abstract
Numerical viscosity has long been a problem in fluid animation. Existing methods suffer from intrinsic artificial dissipation and often apply complicated computational mechanisms to combat such effects. Consequently, dissipative behavior cannot be controlled or modeled explicitly in a manner independent of time step size, complicating the use of coarse previews and adaptive time-stepping methods. This paper proposes simple, unconditionally stable, fully Eulerian integration schemes with no numerical viscosity that are capable of maintaining the liveliness of fluid motion without recourse to corrective devices. Pressure and fluxes are solved efficiently and simultaneously in a time-reversible manner on simplicial grids, and the energy is preserved exactly over long time scales in the case of inviscid fluids. These integrators can be viewed as an extension of the classical energy-preserving Harlow-Welch / Crank-Nicolson scheme to simplicial grids.
BibTeX
@article{Mullen:2009:EIF,
author = {Mullen, Patrick and Crane, Keenan and Pavlov, Dmitry and Tong, Yiying and Desbrun, Mathieu},
title = {Energy-preserving integrators for fluid animation},
journal = {ACM Trans. Graph.},
volume = {28},
number = {3},
month = {July},
year = {2009},
}
Multiscale 3D Reference Visualization
 Glueck,
Crane,
Anderson,
Rutnik,
Khan
Glueck,
Crane,
Anderson,
Rutnik,
Khan
i3D (2009)
Abstract
Reference grids are commonly used in design software to help users to judge distances and to understand the orientation of the virtual workspace. However, despite their ubiquity in 3D graphics authoring applications, little research has gone into important design considerations of the 3D reference grids themselves, which directly impact their usefulness. In an effort to resolve some of these outstanding issues, we have developed two new techniques; the multiscale reference grid and position pegs that form a consistent foundation for presenting relative scale and position information to the user.
Our design of a multiscale reference grid consistently subdivides and coalesces gridlines, based on the computation of a closeness metric, while ensuring that there are neither too many nor too few subdivisions. Position pegs extend the grid so that objects that are lying above or below the ground plane can be brought into a common environmental frame of reference without interfering with the grid or object data. We introduce an analytical system, similar to MIP mapping, to provide a stable viewpoint-determined result. Our design solves several depth cue problems in a way that is independent of viewing projection.
BibTeX
@inproceedings{Glueck:2009:MRV,
author = {Glueck, Michael and Crane, Keenan and Anderson, Sean and Rutnik, Andres and Khan, Azam},
title = {Multiscale 3D reference visualization},
booktitle = {Proceedings of the 2009 symposium on Interactive 3D graphics and games},
series = {I3D '09},
year = {2009},
isbn = {978-1-60558-429-4},
location = {Boston, Massachusetts},
pages = {225--232},
numpages = {8},
url = {http://doi.acm.org/10.1145/1507149.1507186},
doi = {http://doi.acm.org/10.1145/1507149.1507186},
acmid = {1507186},
publisher = {ACM},
address = {New York, NY, USA},
}
Capturing and Animating
Occluded Cloth
 White,
Crane,
Forsyth
White,
Crane,
Forsyth
ACM Trans. on Graph. (2007)
Abstract
We capture the shape of moving cloth using a custom set of color markers printed on the surface of the cloth. The output is a sequence of triangle meshes with static connectivity and with detail at the scale of individual markers in both smooth and folded regions. We compute markers' coordinates in space using marker correspondence across multiple synchronized video cameras. Correspondence is determined from color information in small neighborhoods and refined using a novel strain pruning process. Final correspondence does not require neighborhood information. We use a novel data driven hole-filling technique to fill occluded regions. Our results include several challenging examples: a wrinkled shirt sleeve, a dancing pair of pants, and a rag tossed onto a cup. Finally, we demonstrate that cloth capture is reusable by animating a pair of pants using human motion capture data.
BibTeX
@article{White:2007:CAO,
author = {White, Ryan and Crane, Keenan and Forsyth, D. A.},
title = {Capturing and animating occluded cloth},
journal = {ACM Trans. Graph.},
volume = {26},
number = {3},
month = {July},
year = {2007},
}
Data Driven Cloth Animation
 White,
Crane,
Forsyth
White,
Crane,
Forsyth
SIGGRAPH 2007 Technical Sketches
Abstract
We present a new method for cloth animation based on data driven synthesis. In contrast to approaches that focus on physical simulation, we animate cloth by manipulating short sequences of existing cloth animation. While our source of data is cloth animation captured using video cameras, the method is equally applicable to simulation data. The approach has benefits in both cases: current cloth capture is limited because small tweaks to the data require filming an entirely new sequence. Likewise, simulation suffers from long computation times and complications such as tangling. In this sketch we create new animations by fitting cloth animation to human motion capture data, i.e., we drive the cloth with a skeleton.
BibTeX
@inproceedings{White:2007:DDC,
author = {White, Ryan and Crane, Keenan and Forsyth, D. A.},
title = {Data driven cloth animation},
booktitle = {ACM SIGGRAPH 2007 sketches},
series = {SIGGRAPH '07},
year = {2007},
location = {San Diego, California},
articleno = {37},
acmid = {1278825},
publisher = {ACM},
address = {New York, NY, USA},
}
Real Time Simulation and
Rendering of 3D Fluids
 Crane,
Llamas,
Tariq
Crane,
Llamas,
Tariq
GPU Gems 3 (2007)
Abstract
Physically based animation of fluids such as smoke, water, and fire provides some of the most stunning visuals in computer graphics, but has historically been the domain of high-quality offline rendering due to great computational cost. In this chapter we not only show how these effects can be simulated and rendered in real time, but also how they can be seamlessly integrated into real time applications.
BibTeX
@InBook{Crane07,
author = "Crane, Keenan and Llamas, Ignacio, and Tariq, Sarah",
title = "Real Time Simulation and Rendering of 3D Fluids",
booktitle = "GPUGems 3",
editor = "Hubert Nguyen",
chapter = "30",
publisher = "Addison-Wesley",
year = "2007"
}
Rectangular Multi-Chart
Geometry Images
 Carr,
Hoberock,
Crane,
Hart
Carr,
Hoberock,
Crane,
Hart
Symp. on Geom. Proc. (2006)
Abstract
Many mesh parameterization algorithms have focused on minimizing distortion and utilizing texture area, but few have addressed issues related to processing a signal on the mesh surface. We present an algorithm which partitions a mesh into rectangular charts while preserving a one-to-one texel correspondence across chart boundaries. This mapping permits any computation on the mesh surface which is typically carried out on a regular grid, and prevents seams by ensuring resolution continuity along the boundary. These features are also useful for traditional texture applications such as surface painting where continuity is important. Distortion is comparable to other parameterization schemes, and the rectangular charts yield efficient packing into a texture atlas. We apply this parameterization to texture synthesis, fluid simulation, mesh processing and storage, and locating geodesics.
BibTeX
@inproceedings{Carr:2006:RMG,
author = {Carr, Nathan A. and Hoberock, Jared and Crane, Keenan and Hart, John C.},
title = {Rectangular Multi-Chart Geometry Images},
booktitle = {Proceedings of the fourth Eurographics symposium on Geometry processing},
year = {2006},
}
Fast GPU Ray Tracing of Dynamic
Meshes using Geometry Images
 Carr,
Hoberock,
Crane,
Hart
Carr,
Hoberock,
Crane,
Hart
Graphics Interface 2006
Abstract
Using the GPU to accelerate ray tracing may seem like a natural choice due to the highly parallel nature of the problem. However, determining the most versatile GPU data structure for scene storage and traversal is a challenge. In this paper, we introduce a new method for quick intersection of triangular meshes on the GPU. The method uses a threaded bounding volume hierarchy built from a geometry image, which can be efficiently traversed and constructed entirely on the GPU. This acceleration scheme is highly competitive with other GPU ray tracing methods, while allowing for both dynamic geometry and an efficient level of detail scheme at no extra cost.
BibTeX
@inproceedings{Carr:2006:FGR,
author = {Carr, Nathan A. and Hoberock, Jared and Crane, Keenan and Hart, John C.},
title = {Fast GPU ray tracing of dynamic meshes using geometry images},
booktitle = {Proceedings of Graphics Interface 2006},
series = {GI '06},
year = {2006},
isbn = {1-56881-308-2},
location = {Quebec, Canada},
pages = {203--209},
numpages = {7},
url = {http://portal.acm.org/citation.cfm?id=1143079.1143113},
acmid = {1143113},
publisher = {Canadian Information Processing Society},
address = {Toronto, Ont., Canada, Canada},
}
A Two-Color Map of Pluto's
Sub-Charon Hemisphere
 Young,
Binzel,
Crane
Young,
Binzel,
Crane
The Astronomical Journal (2001)
Abstract
Pluto and its satellite Charon regularly occulted or transited each other's disks from 1985 through 1990. The light curves resulting from these events (collectively called "mutual events") have been used to determine albedo maps of Pluto's sub-Charon hemisphere. We now use a data set of four light curves that were obtained in both B and V Johnson filters to construct a two-color map of Pluto's surface. We are able to resolve the central part of Pluto's sub-Charon hemisphere. We find that the dark albedo feature that forms a band below Pluto's equator is comprised of several distinct color units. We detect ratios of V-filter/B-filter normal reflectances ranging from 1.15 to 1.39 on Pluto's sub-Charon hemisphere.
BibTeX
@article{1538-3881-121-1-552,
author={Eliot F. Young and Richard P. Binzel and Keenan Crane},
title={A Two-Color Map of Pluto's Sub-Charon Hemisphere},
journal={The Astronomical Journal},
volume={121},
number={1},
pages={552},
url={http://stacks.iop.org/1538-3881/121/i=1/a=552},
year={2001}
}
|