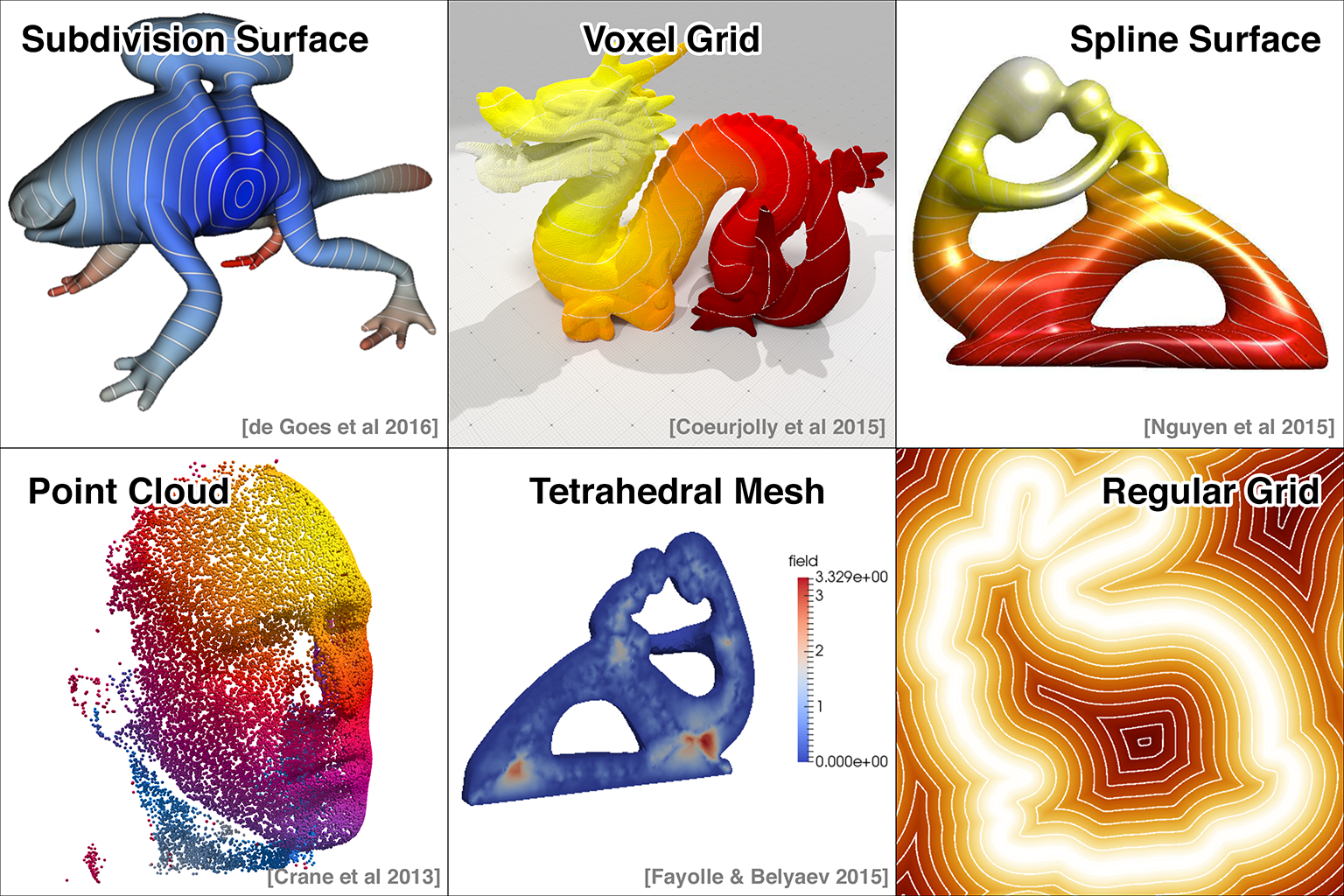
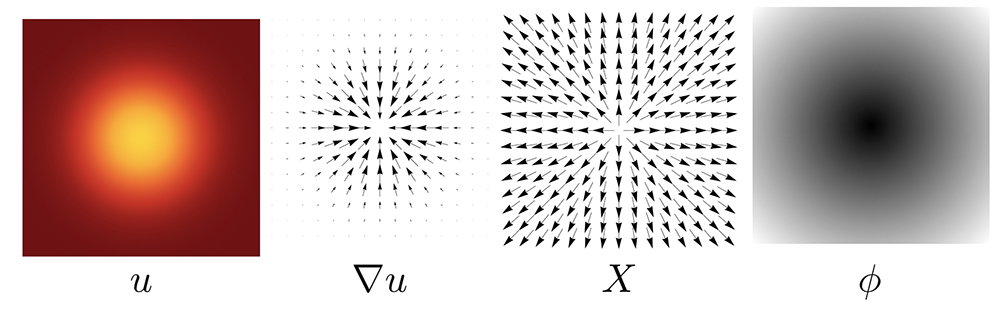
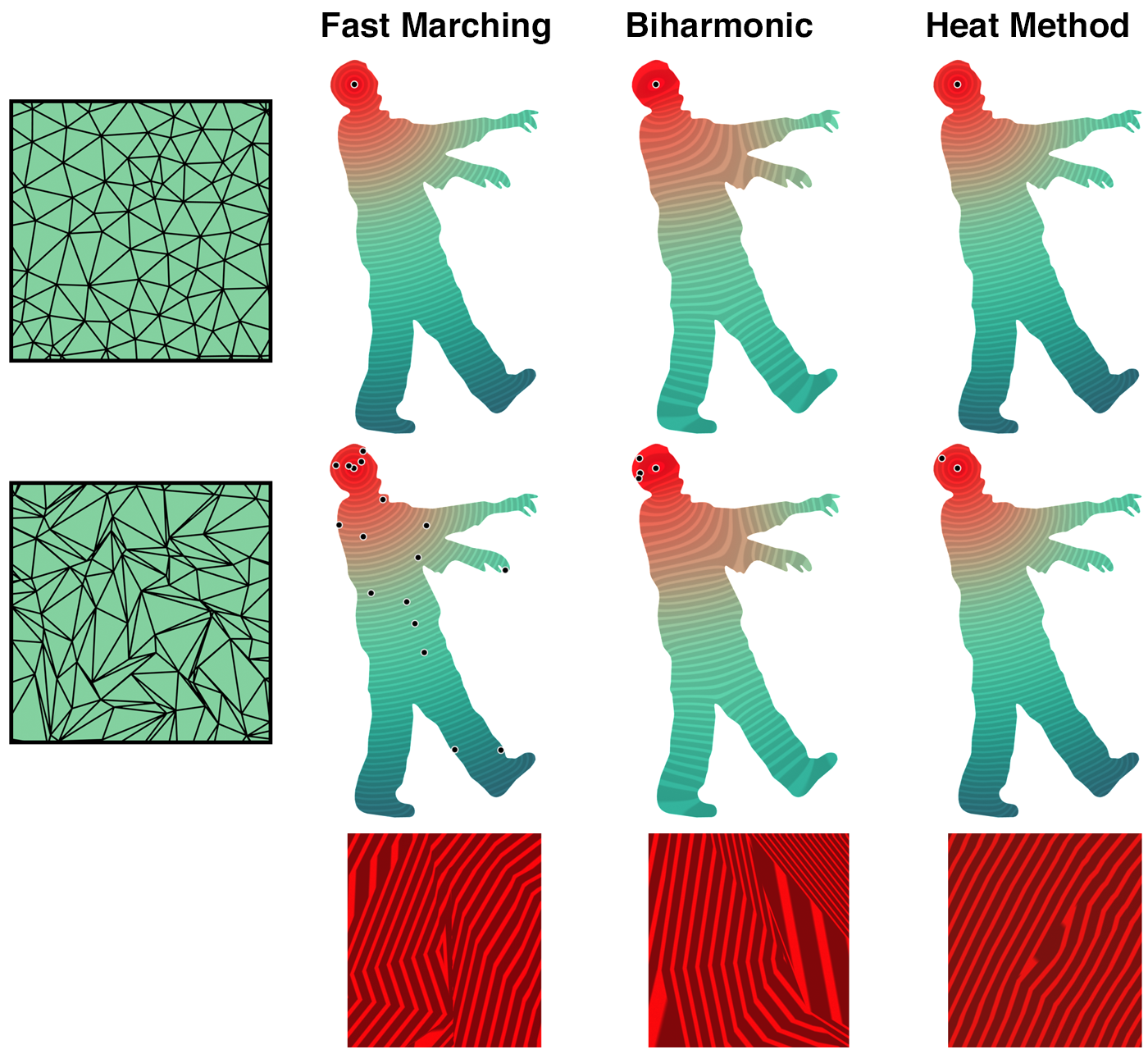
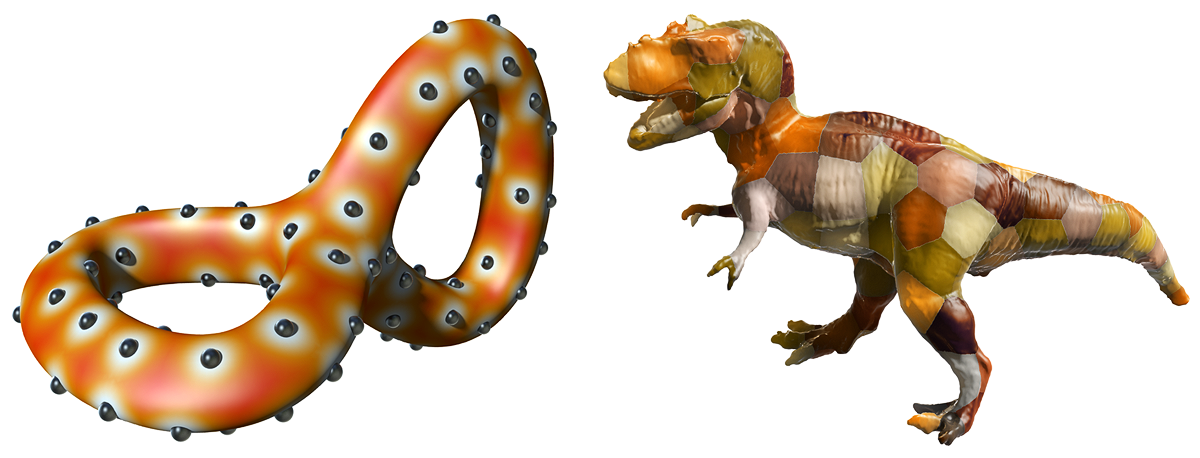In the case of triangle meshes, any modern implementation of the heat method should really make use of the intrinsic Laplace operator, which adds negligible computational overhead, and has identical inputs/outputs, but is much (much) more robust on low-quality meshes. The GeometryCentral, CGAL, and libigl implementations listed below provide this option. The GeometryCentral version also works on general meshes, including non-manifold ones, by adopting the tufted Laplacian.
None of the current implementations of the heat method (listed on this page) fully exploit its potential for speed or accuracy. To substantially improve performance on multi-core or GPU-based systems, one need only link against a parallel sparse linear solver that can handle symmetric positive-definite systems. (One might also parallelize matrix construction.) To further improve accuracy, one can incorporate the very nice iterative scheme of Belyaev & Fayolle from their paper On Variational and PDE-Based Distance Function Approximations. Like the heat method, this scheme lends itself nicely to prefactorization (hence low amortized cost relative to fast marching/fast sweeping or window-based methods), and would be easy to implement on top of the existing reference implementation.
For a very cool application of the heat method, see Floraform.
It is also possible to use the heat method to solve the single- or multiple-source shortest path problem on general graphs.
(courtesy Oleg Memukhin)
| JavaScript— | interactive version running in-browser (requires WebGL support). |
| geometry-central— | robust C++ implementation (with optional Python bindings) that works on low-quality and non-manifold meshes. |
| point clouds— | implementation in geometry-central (C++ with optional Python bindings). Computes geodesic distance directly on point clouds, as well as other quantities like scalar extension, vector extension, and the log map via the vector heat method. |
| ANSI C— | optimized reference implementation written by the authors; depends on an external linear solver like CHOLMOD or HSL MA87. |
| CGAL— | C++ implementation in the Computational Geometry Algorithms Library (CGAL). This version uses the intrinsic Laplacian of Bobenko & Springborn to improve accuracy on low-quality meshes. |
| libigl— | header-only C++ implementation in the libigl geometry processing library. Like CGAL, this version (optionally) uses an intrinsic Delaunay triangulation to improve accuracy and robustness. |
| Houdini— | the heat method is built in to SideFX Software's Houdini package, as a “Heat Geodesic” geometry node. |
| Python— | from PyCortex package for cortical processing (Alex Huth/Gallant Lab) |
| MATLAB— | from Gabriel Peyré's Numerical Tours |
| Mathematica— | answer by John Dunlop on StackExchange |
| Mathematica— | written by Henrik Schumacher. |
| C++— | from StarLab |
| C++— | from our SIGGRAPH course |
| Unity— [Mac] [Windows] [Linux] | Cool interactive demo by Ruoqi He & Chia-Man Hung from Ecole Polytechnique. |
| Grasshopper/Rhino— | Implementation by Daniel Piker, solved using a simple iterative scheme. |