The Vector Heat Method
ACM Transactions on Graphics (2019)

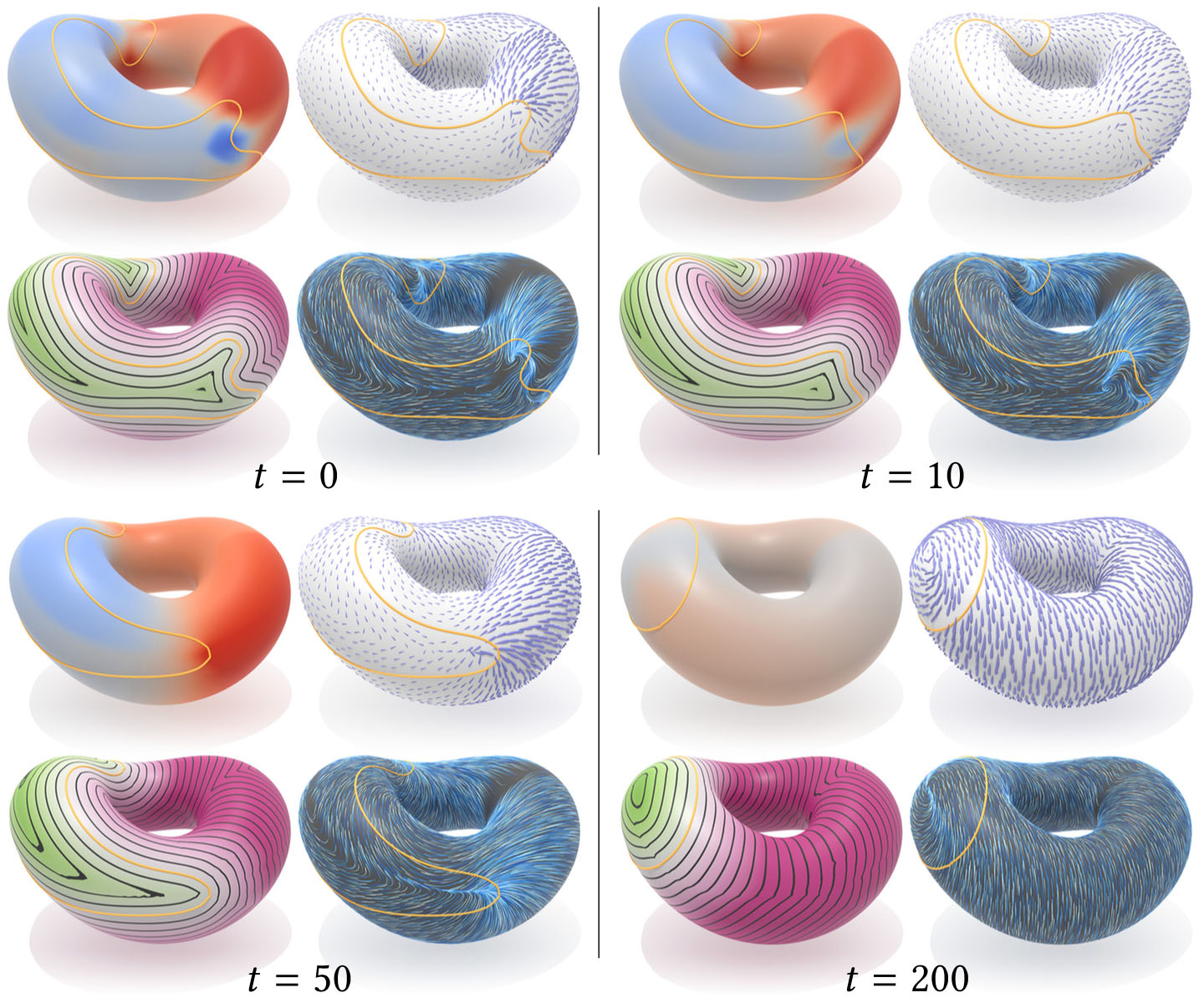
This paper describes a method for efficiently computing parallel transport of tangent vectors on curved surfaces, or more generally, any vector-valued data on a curved manifold. More precisely, it extends a vector field defined over any region to the rest of the domain via parallel transport along shortest geodesics. This basic operation enables fast, robust algorithms for extrapolating level set velocities, inverting the exponential map, computing geometric medians and Karcher/Fréchet means of arbitrary distributions, constructing centroidal Voronoi diagrams, and finding consistently ordered landmarks. Rather than evaluate parallel transport by explicitly tracing geodesics, we show that it can be computed via a short-time heat flow involving the connection Laplacian. As a result, transport can be achieved by solving three prefactored linear systems, each akin to a standard Poisson problem. To implement the method we need only a discrete connection Laplacian, which we describe for a variety of geometric data structures (point clouds, polygon meshes, etc.). We also study the numerical behavior of our method, showing empirically that it converges under refinement, and augment the construction of intrinsic Delaunay triangulations (iDT) so that they can be used in the context of tangent vector field processing.
The Heat Method for Distance Computation - the original heat method paper provides a nice introduction to the principle of computation from diffusion (as well as some useful implementation details).
Teaser Video
Presentation
Heat Methods Overview
vector-heat-demo—C++ implementation and interactive demo, including parallel transport and the log map, with visualization in Polyscope.
@article{Sharp:2019:VHM,
author = {Sharp, Nicholas and Soliman, Yousuf and Crane, Keenan},
title = {The Vector Heat Method},
journal = {ACM Trans. Graph.},
volume = {38},
number = {3},
year = {2019},
publisher = {ACM},
address = {New York, NY, USA},
}
Thanks to Jooyoung Hahn for early discussions about signed distance computation, and Jim McCann for project feedback. This work was supported by a Packard Fellowship, NSF Award 1717320, an NSF Graduate Research Fellowship, and gifts from Autodesk, Adobe, and Facebook.
Figures

Parallel transport of vectors from points (left) and curves (right).

Left: one application of the heat method is to compute the logarithmic map (also sometimes referred to as the exponential map), which provides a coordinate system on the surface relative to a chosen origin x. Right: on the sphere we easily compute the correct log map; note that far from the source even the analytical log map can be highly skewed.
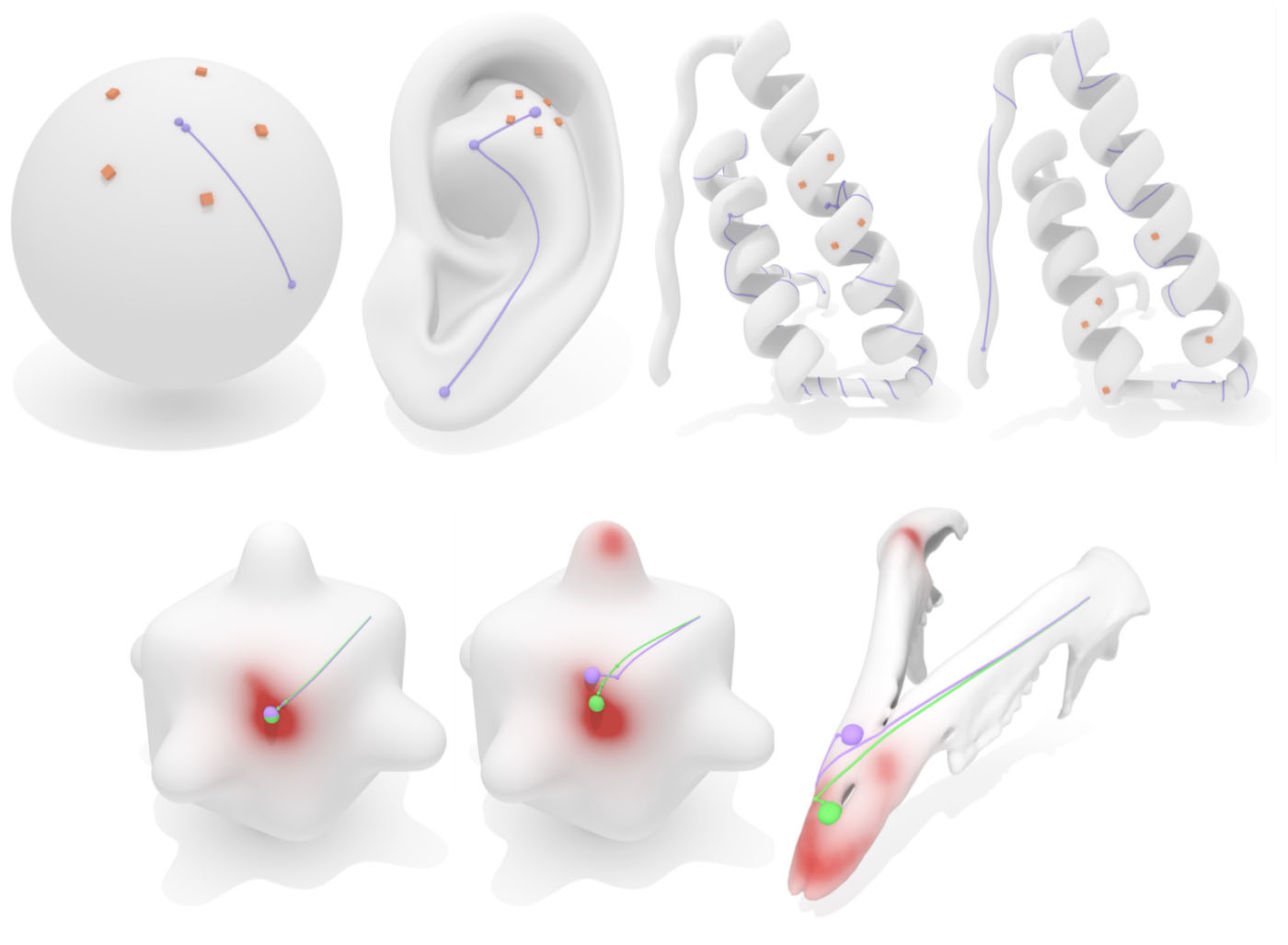
Our globally accurate logarithmic map can be used to compute centers of data on a curved surface. Left: given a collection of points, we iteratively compute the Karcher mean; on simple geometries we reproduce the expected solution in just 2-3 iterations, and the algorithm generalizes to more complex geometries while still needing less than 20 iterations. Right: We can also efficiently compute the centers of distributions; here we show both the Karcher mean (purple) and the geometric median (green). The Karcher mean is significantly influenced by outliers, while the geometric median is not.
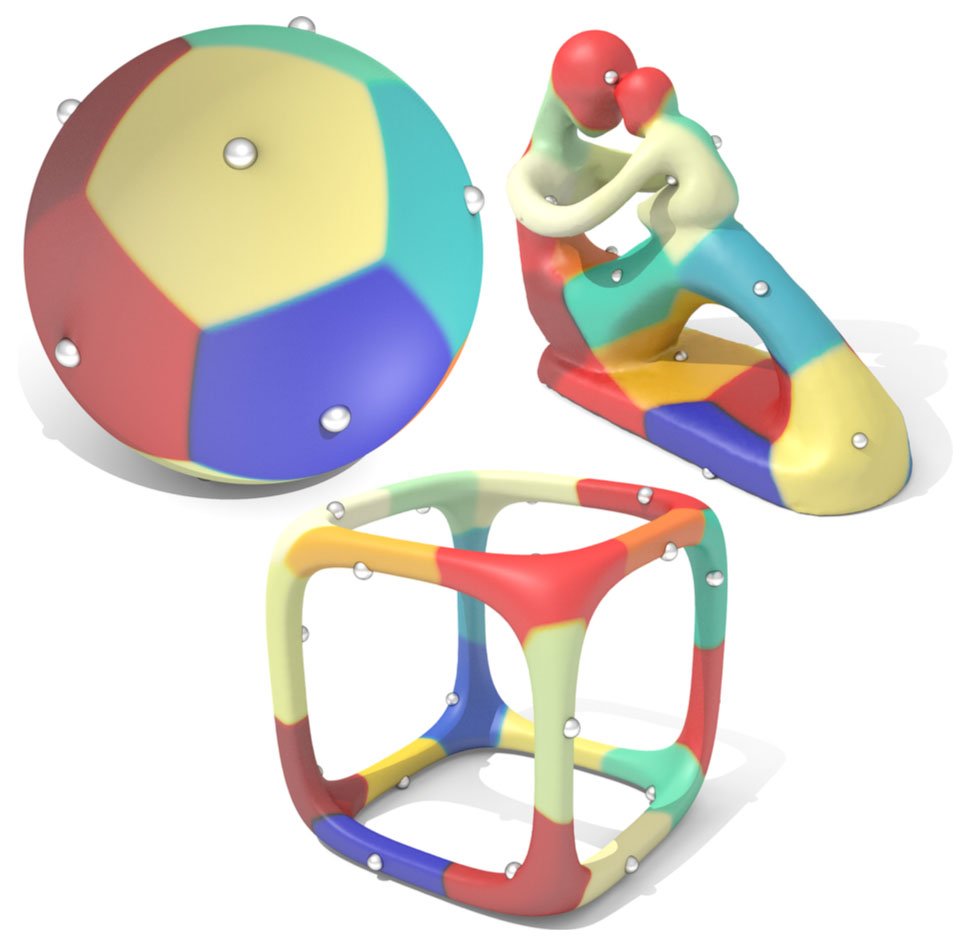
Fast Karcher means allow us to compute centroidal geodesic Voronoi tessellations with large, possibly multiply-connected cells.
Our robust geometric median facilitates computation of consistently ordered landmarks, helping to avoid difficult matching problems.
Our method also enables fast velocity extension for level set methods. Here we show a sequence of frames from a simple curve-shortening flow, plus a constant tangential term. In each frame, our scalar interpolation scheme provides a closest-point interpolation of normal velocity (top left), resulting in excellent preservation of the signed distance function over long integration times (bottom left); note that we never apply explicit redistancing. Since the vector heat method provides accurate extrapolation of vector data over the entire domain (top right), we can track particles even very far from the interface (bottom right).

To implement the vector heat method on a given geometric data structure, we essentially just need a scalar Laplacian and a notion of tangent spaces at each point or vertex. Here we show the solution for three sources of di erent magnitudes on a triangle mesh, point cloud, polygon mesh, and voxelization.
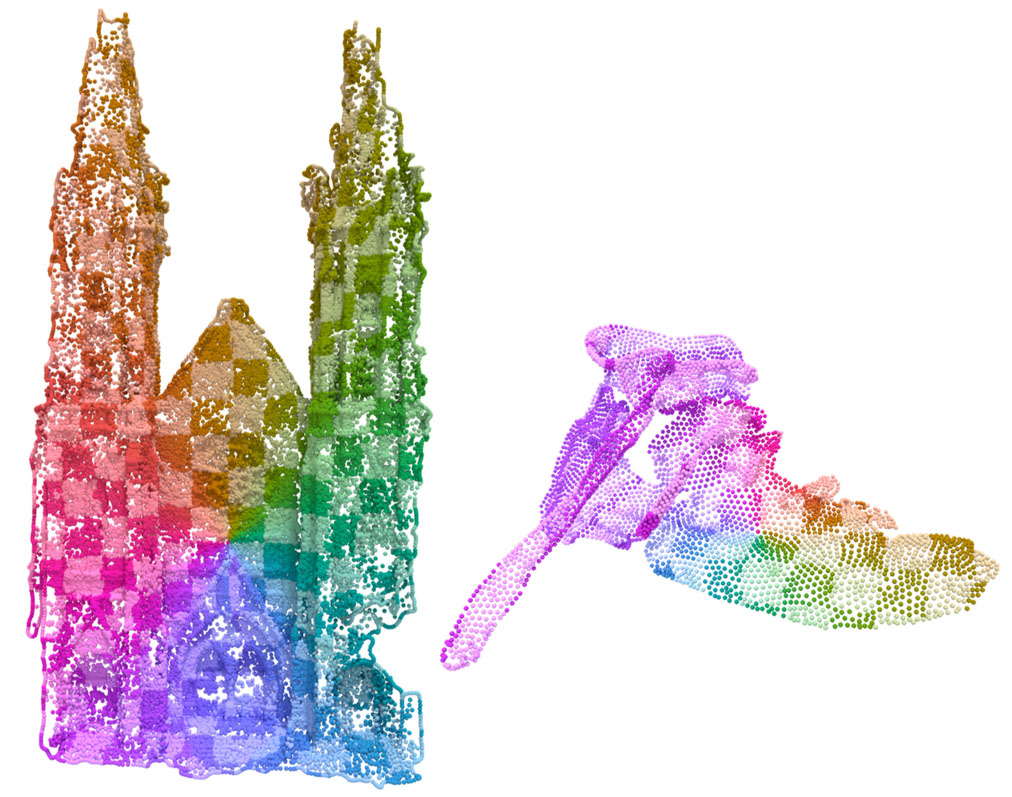
Other point cloud algorithms, such as computing a local parameterization (shown here, using the log map) can then be implemented on top of the vector heat method with little to no additional work.
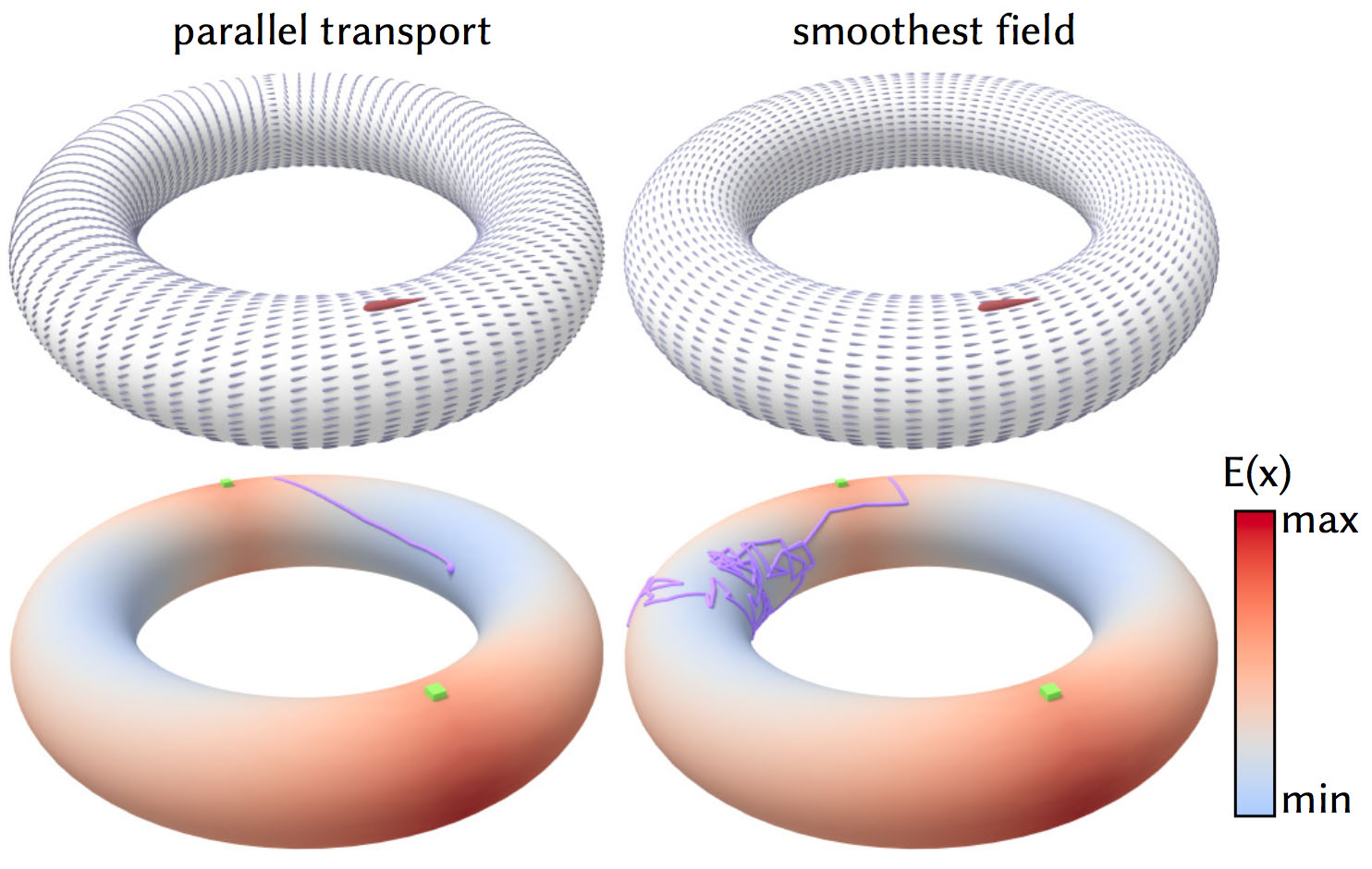
The field obtained by parallel transport along shortest geodesics plays a special role in several basic geometric algorithms—replacing it with a field that is merely smooth can cause these algorithms to fail. Here for instance we use the field to locate the Karcher mean equidistant from the two green points (left). Attempting to instead use the smoothest possible field causes this search to fail, wandering randomly over the surface (right).

Even just tracing all the geodesics to a given source point (without accounting for the cost of distance computation) is already an order of magnitude more expensive than applying the vector heat method—here, 15x slower.
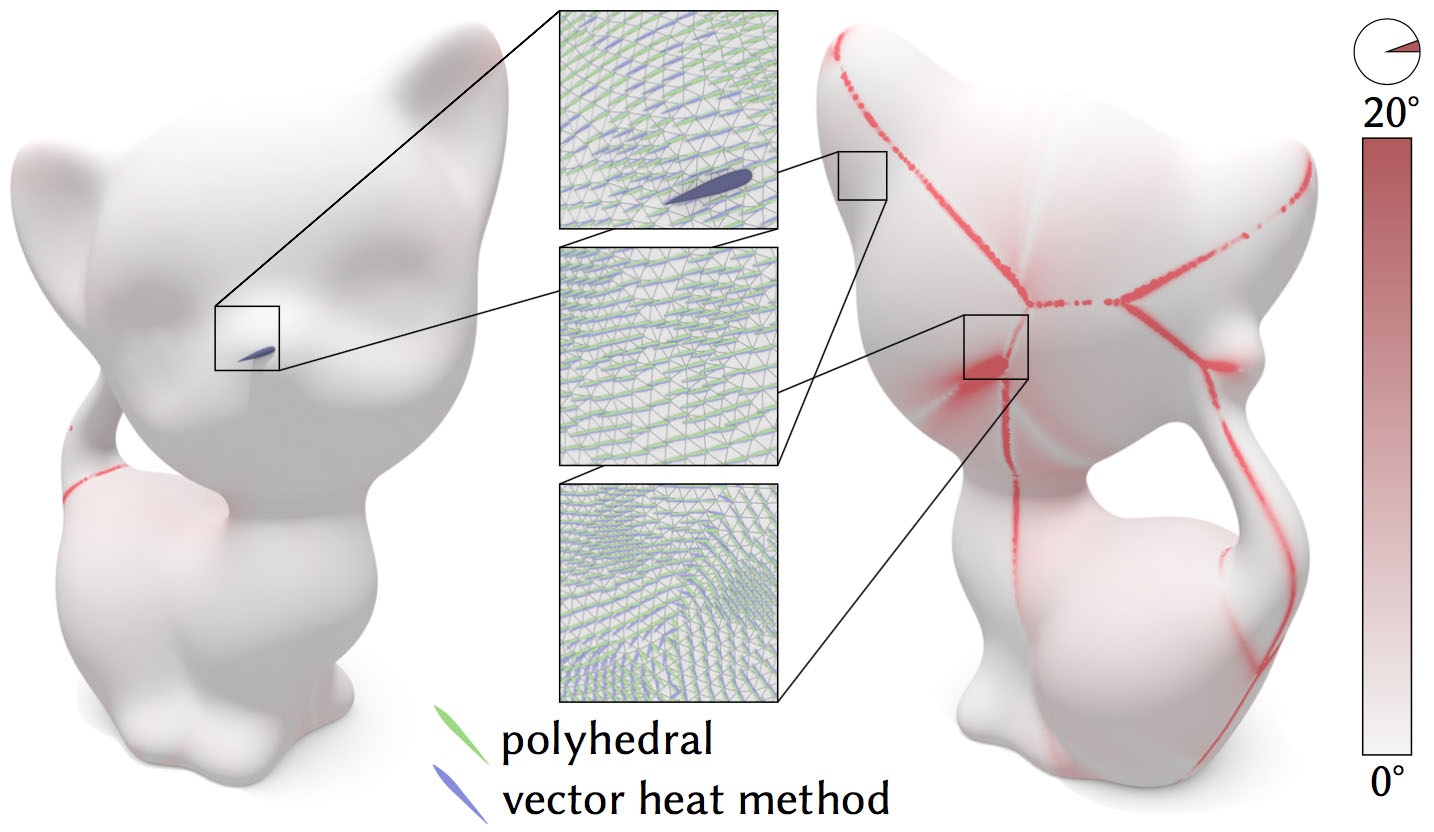
Our algorithm yields very similar results to the brute-force approach of explicitly unfolding triangles along exact polyhedral geodesics. Away from the cut locus, the difference is typically just a few degrees (left, right).
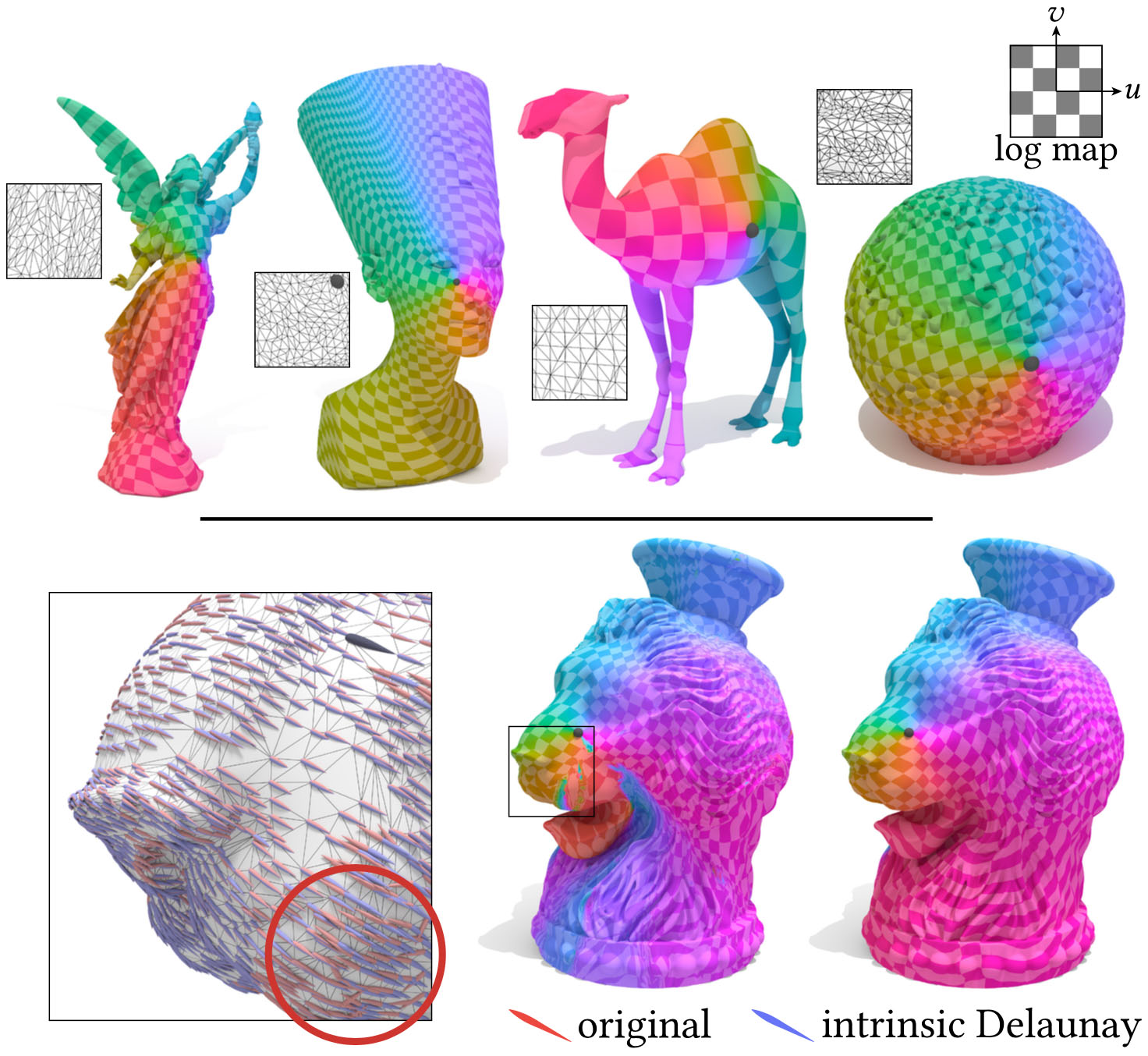
We often obtain high-quality results even on non-Delaunay meshes (top). Occasionally, however, transported fields can have improperly oriented vectors (inset), here causing errors in the log map (bottom center). By keeping track of tangent spaces during intrinsic Delaunay flips, we obtain a high-quality solution (bottom right) without having to change the input geometry.

Results of the vector heat method on a variety of models; source is marked by a large arrow. For visualization, vectors are sampled à la Bridson [2007].
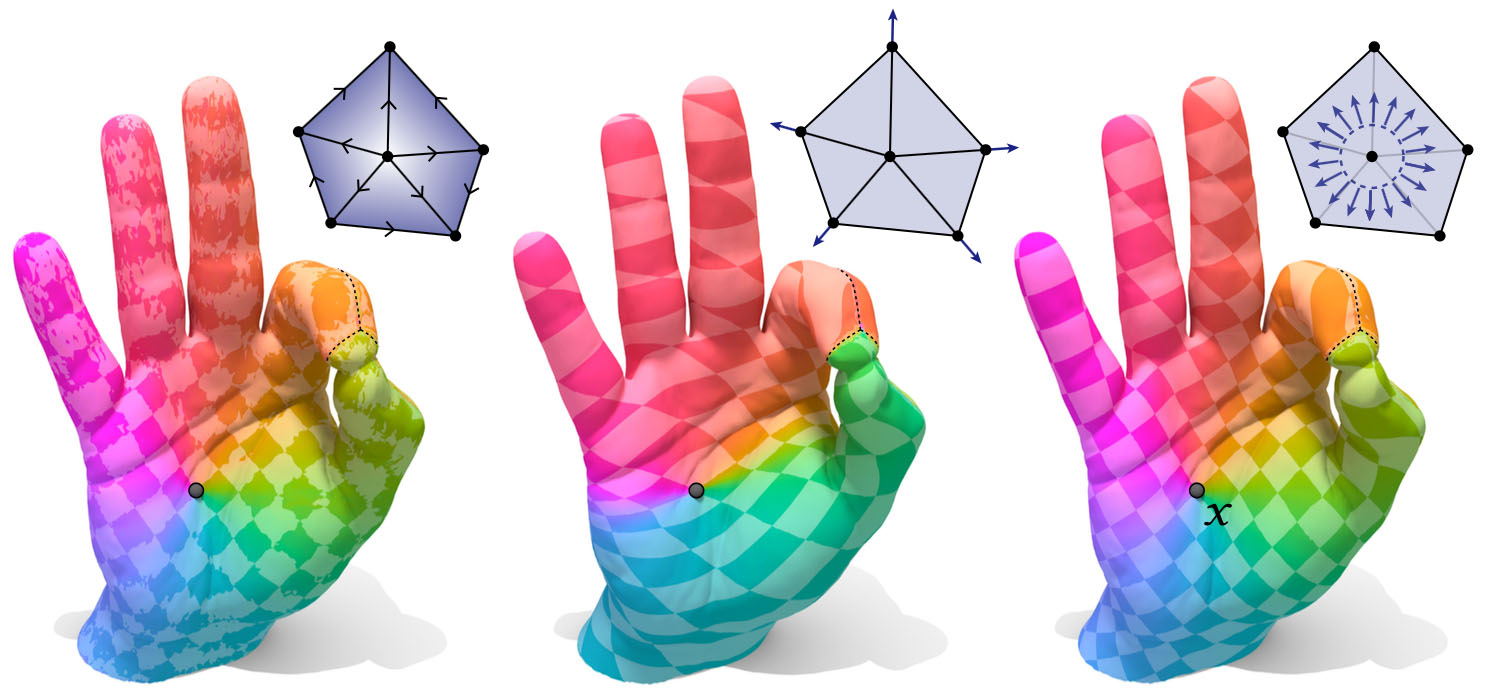
To get a high-quality log map (here, from a source point x) one must carefully discretize the distance gradient. Left: simply taking the gradient of a given distance function yields numerical noise. Middle: naive parallel transport of vectors emanating from the source yields global anisotropy. Right: proper discretization of initial conditions yields a smooth and accurate map, where the only remaining noise is near the cut locus (dashed line).
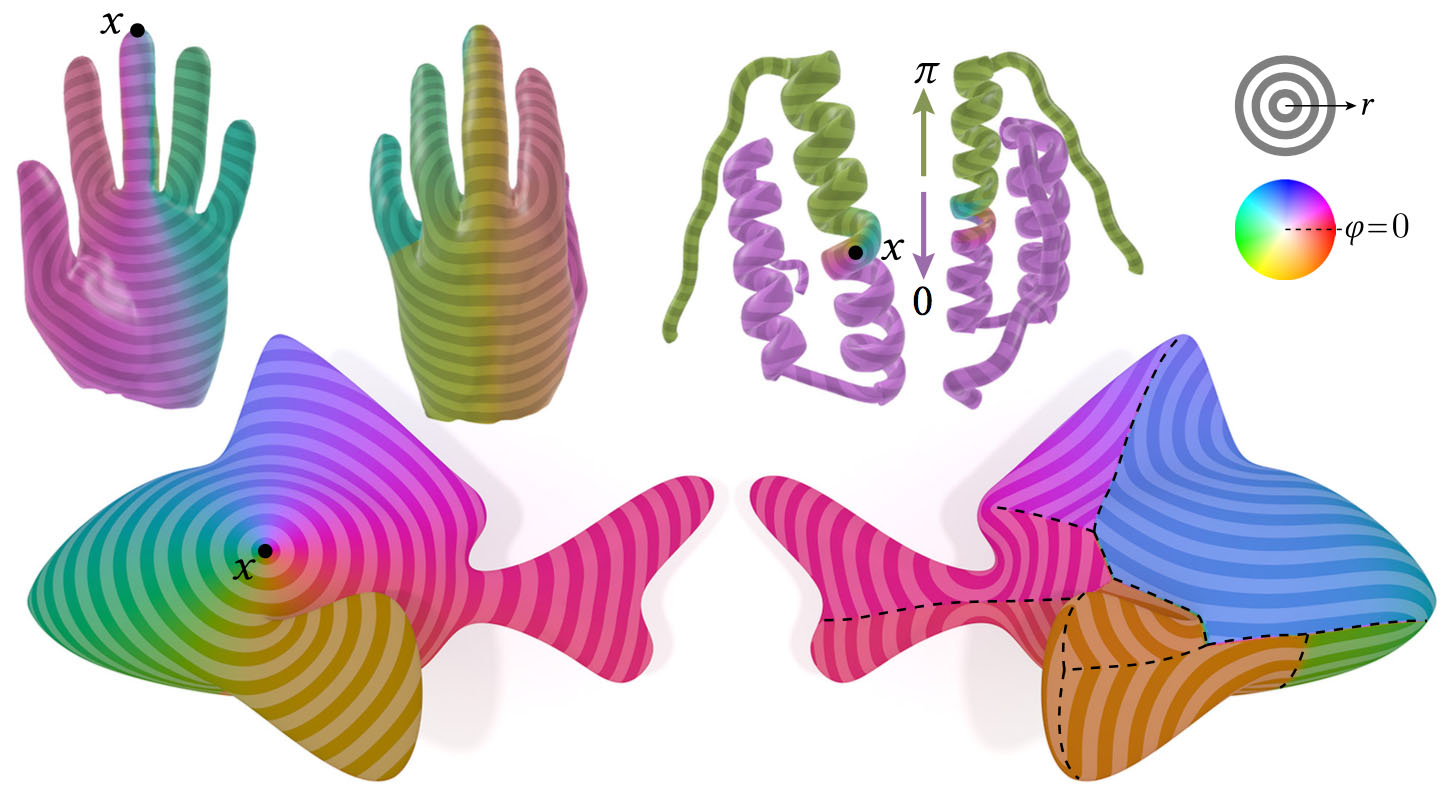
Our log map is globally accurate—even on long skinny models where most points are reached by traveling in nearly identical directions (far right). On a high-resolution mesh we nicely resolve the cut locus (dashed line).
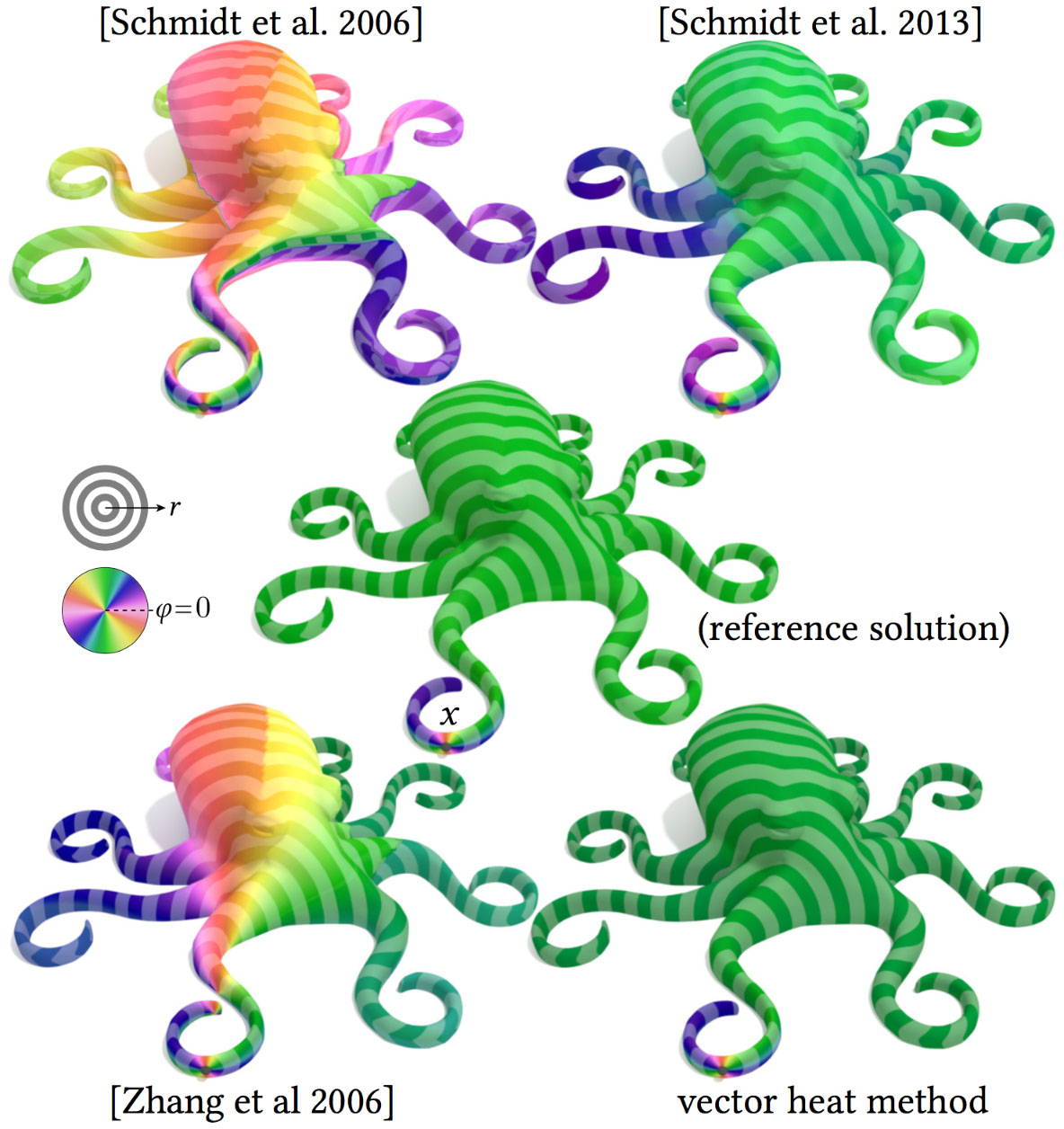
Since the vector heat method is based on a straightforward discretization of a smooth formulation, it leads to a close approximation of the true log map. Previous approximations exhibit not only small local errors, but large global inaccuracies—especially in the angular coordinate φ. (Reference solution is computed via the exact polyhedral scheme.)
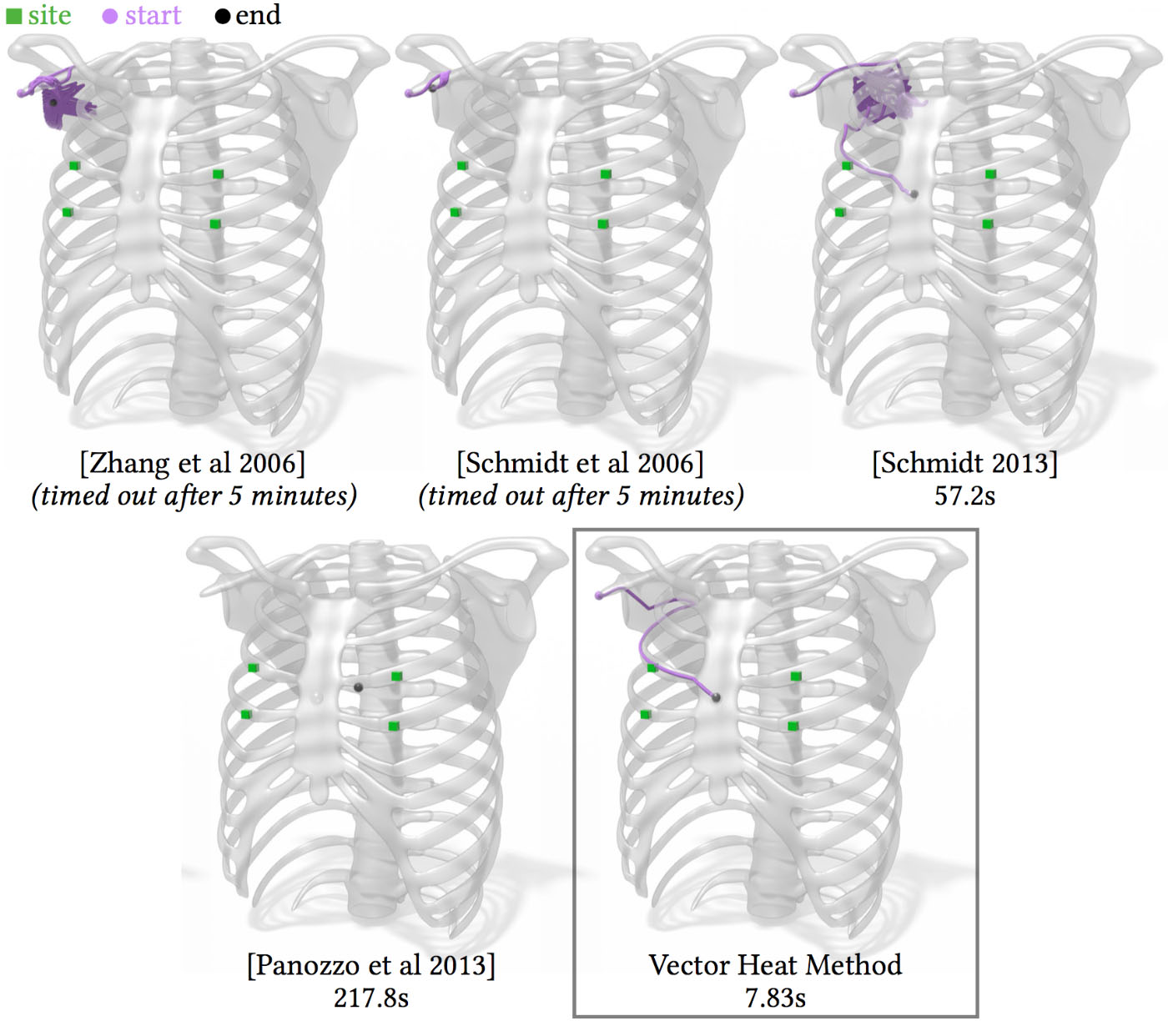
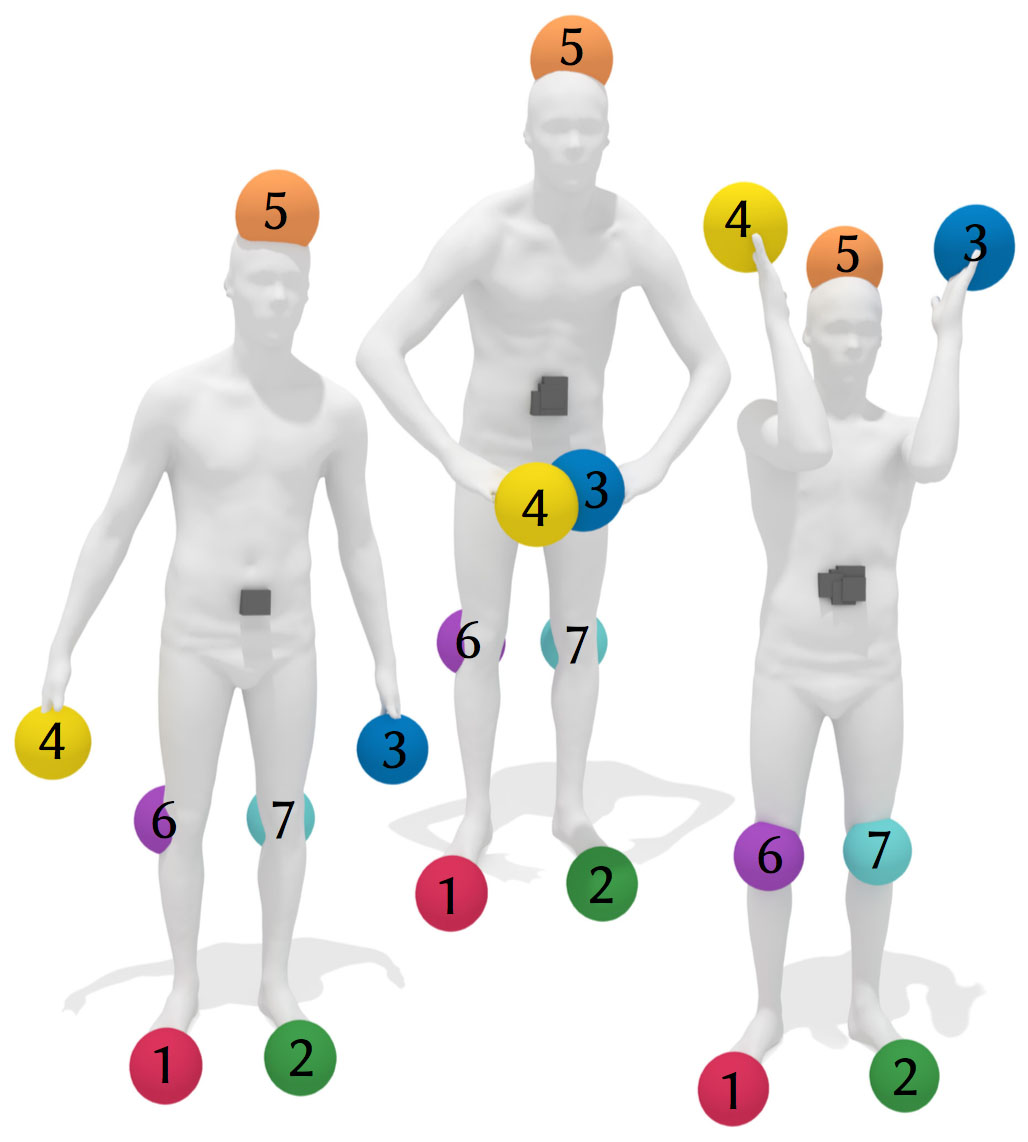
Here we compute the Karcher mean of the four green points, which should appear at the center of the sternum. Previous local approximations of the log map yield poor behavior, with iterates failing to converge (far left, center left) or wandering around randomly until line search pushes the solution toward a local minimum (center). Other algorithms compute only approximate averages, which may not respect symmetries of the problem (center right). The global accuracy of the log map provided by the heat method guides the algorithm to the correct solution in just a few iterations (far right).
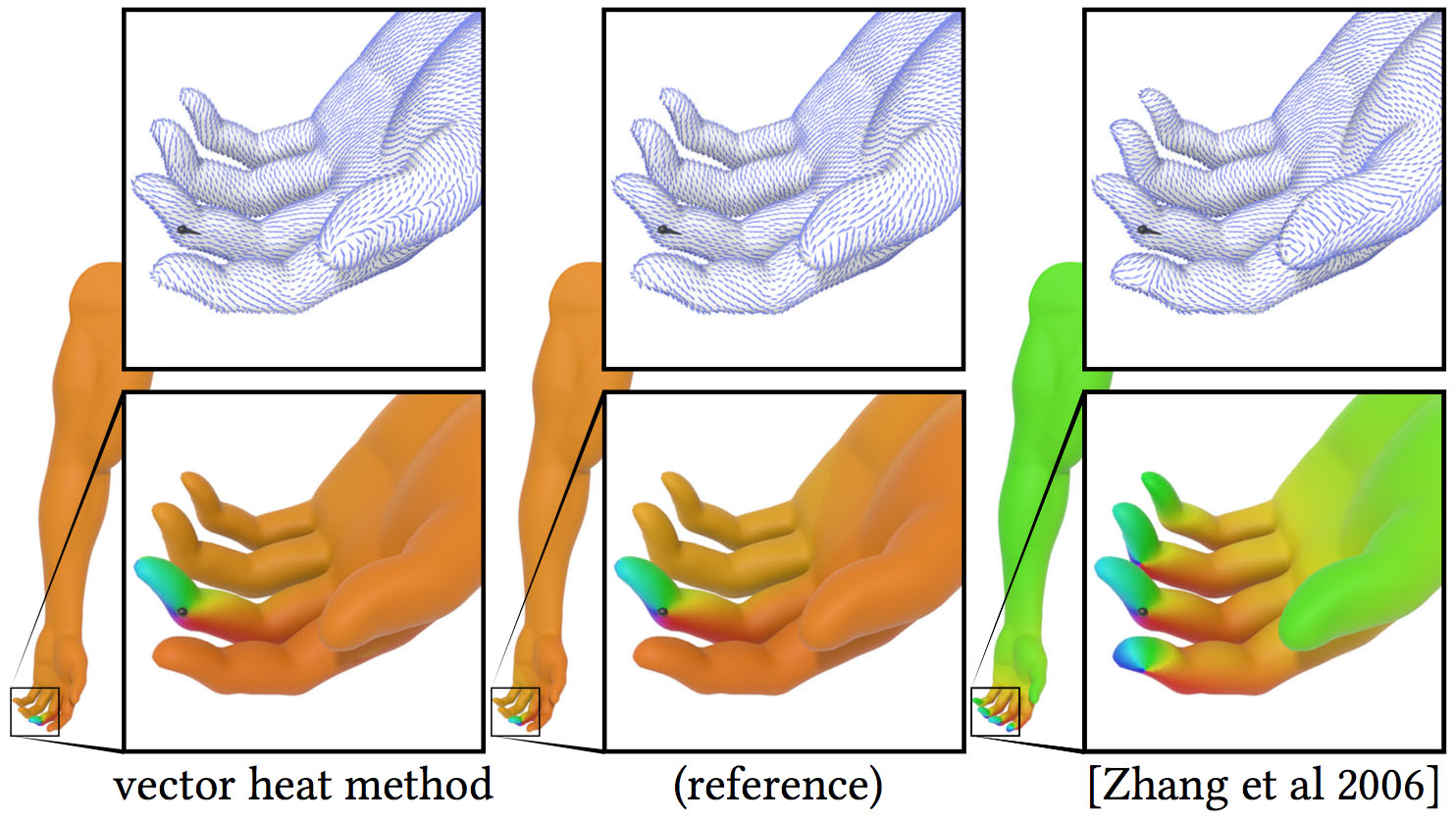
Other local approximations of parallel transport, such as the method of Zhang et al [2006], do not provide a good global approximation over the larger domain. Here the field produced by the vector heat method closely matches the reference (exact polyhedral surface) allowing us to compute a globally accurate log map; the local approximation of Zhang et al deviates significantly away from the source.
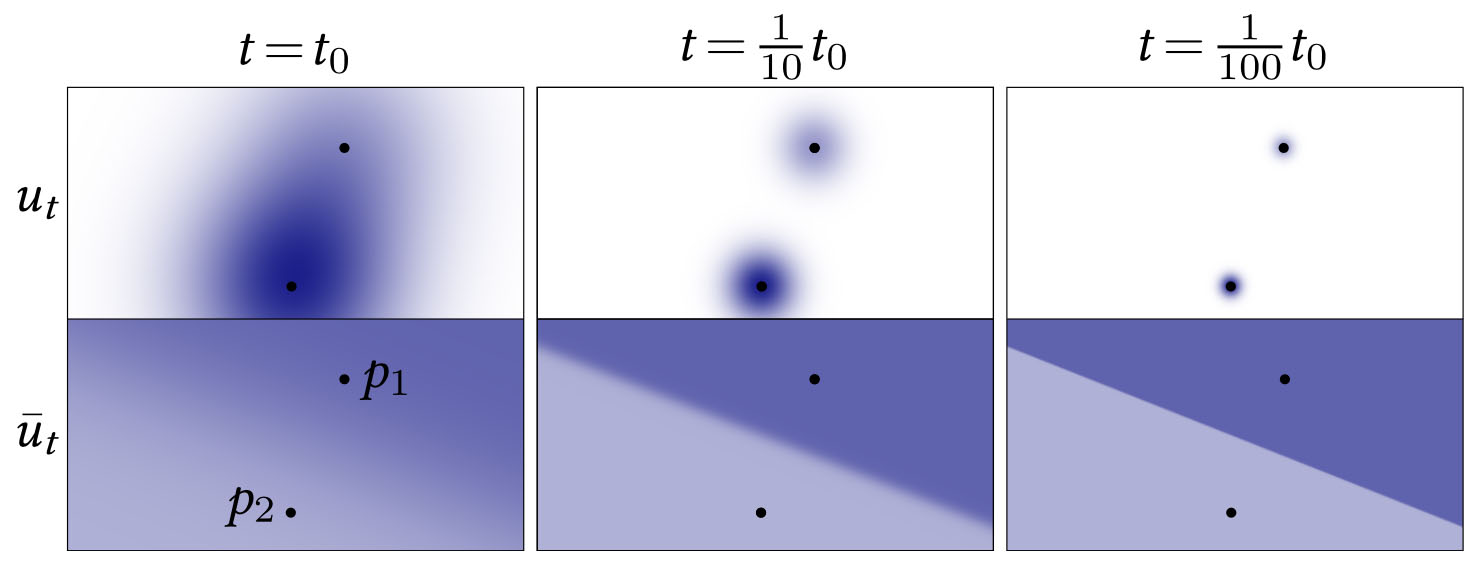
A simple example of interpolation by diffusion: a Gaussian weighted combination of values at two points p1,p2, yields a closest point interpolation ut as the Gaussian width t goes to zero. Here ut is the linear combination prior to normalization.

Interpolation of scalar values at points (left) and curves (right).
