Monte Carlo Geometry Processing:
A Grid-Free Approach to PDE-Based Methods on Volumetric Domains
A Grid-Free Approach to PDE-Based Methods on Volumetric Domains
SIGGRAPH 2020 / ACM Transactions on Graphics 2020
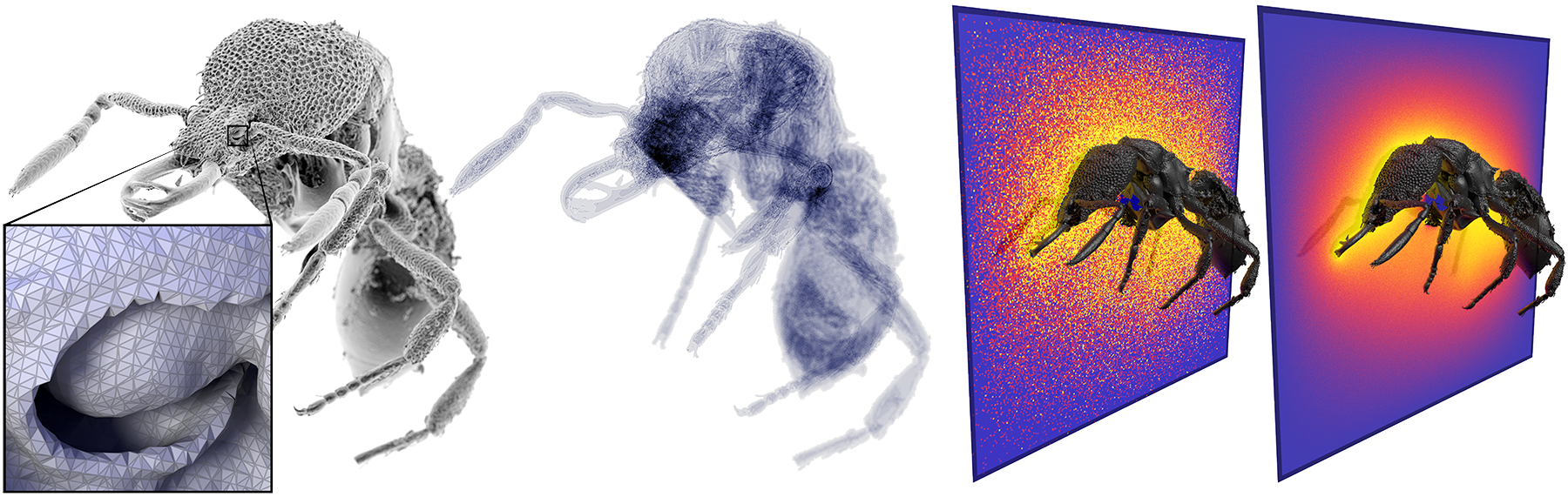
This paper explores how core problems in PDE-based geometry processing can be efficiently and reliably solved via grid-free Monte Carlo methods. Modern geometric algorithms often need to solve Poisson-like equations on geometrically intricate domains. Conventional methods most often mesh the domain, which is both challenging and expensive for geometry with fine details or imperfections (holes, self-intersections, etc.). In contrast, grid-free Monte Carlo methods avoid mesh generation entirely, and instead just evaluate closest point queries. They hence do not discretize space, time, nor even function spaces, and provide the exact solution (in expectation) even on extremely challenging models. More broadly, they share many benefits with Monte Carlo methods from photorealistic rendering: excellent scaling, trivial parallel implementation, view-dependent evaluation, and the ability to work with any kind of geometry (including implicit or procedural descriptions). We develop a complete “black box” solver that encompasses integration, variance reduction, and visualization, and explore how it can be used for various geometry processing tasks. In particular, we consider several fundamental linear elliptic PDEs with constant coefficients on solid regions of Rn. Overall we find that Monte Carlo methods significantly broaden the horizons of geometry processing, since they easily handle problems of size and complexity that are essentially hopeless for conventional methods.
Presentation
Teaser Video
The authors thank Mark Gillespie, Ioannis Gkioulekas, and Rasmus Tamstorf for fruitful conversations, Ruihao Ye for support on closest point queries, and Timothy Sun for some early explorations of these ideas. The hemisus guineensis mesh is used courtesy of the Blackburn Lab, under a CreativeCommons BY 4.0 license. This work was supported by a Packard Fellowship, NSF awards 1717320 and 1943123, and gifts from Autodesk, Adobe, Disney, and Facebook. The second author was also supported by NSF award DMS-1439786 and Sloan award G-2019-11406 while in residence at ICERM.
@article{Sawhney:2020:MCG,
author = {Sawhney, Rohan and Crane, Keenan},
title = {Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains},
journal = {ACM Trans. Graph.},
volume = {39},
number = {4},
year = {2020},
publisher = {ACM},
address = {New York, NY, USA},
}
Tutorial
Web
| WoSLaplace2D.cpp— | quick and dirty version of naïve estimator for 2D Laplace equation. Example output. |
| WoSPoisson2D.cpp— | quick and dirty version of naïve estimator for 2D Poisson equation. Example output. |
| Diffusion curves | —Shadertoy example of 2D diffusion curves, written by Inigo Quilez. (Twitter) |
| Simple Laplace | —Shadertoy example of a simple 2D Laplace equation by Inigo Quilez. (Twitter) |
| Implicit surface | —Shadertoy reproduction of smooth double torus in Figure 2 by Ricky Reusser. (Twitter) |
| Surface inflation | —WoS implementation of Baran & Lehtinen's scheme for inflating curves, by Alec Jacobson. (Twitter) |
Figures
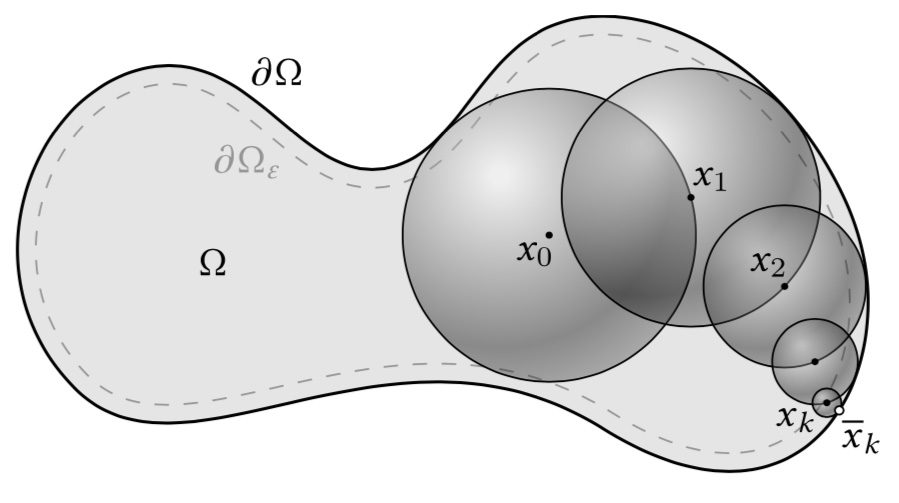
The walk on spheres algorithm repeatedly jumps to a random point on the largest sphere centered at the current point xi , until it gets within ε of the boundary. Since the largest sphere can be determined from a simple closest point query, no spatial discretization is needed.

We can directly solve PDEs on boundary representations not handled by conventional solvers. Left: discontinuous boundary conditions on an implicit surface are captured exactly, whereas FEM or BEM would need a fine mesh to approximate such features. Center: we avoid the daunting challenge of explicit mesh booleans, and can in fact combine heterogeneous representations via constructive solid geometry (CSG). Right: as in rendering, we can compute meaningful solutions for geometry with extremely poor element quality, which degrade gracefully even in the presence of significant noise.
Helmholtz decomposition on a 3D domain. The Monte Carlo approach entirely avoids meshing the domain, setting up matrices, and solving linear systems.

Left: a 3.3M triangle boundary mesh with fine features, from a CT scan of hemisus guineensis (courtesy Blackburn Lab). To visualize the solution to a volumetric PDE, we can significantly reduce cost by computing only a 2D slice of the full 3D solution (right). Inset: fine features are perfectly preserved since we work with the exact input geometry.

Robust meshing methods guarantee success at the cost of geometric accuracy—in this case, completely destroying information about the circulatory and central nervous systems from the previous figure. The Monte Carlo approach exactly preserves these features without hand-tuning of geometric tolerances (nor spending time and memory to precompute a mesh).
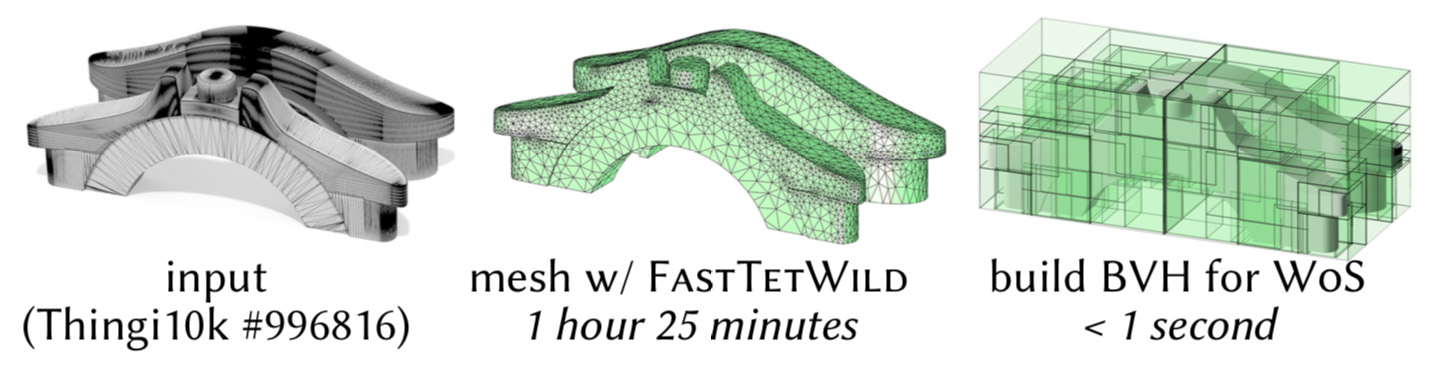
Finite element methods exhibit unpredictable performance, since models with simple geometry but poor element quality (left) can confound even robust meshing algorithms (center). The Monte Carlo approach simply needs to build a standard bounding volume hierarchy (right), dramatically reducing the end-to-end cost of solving a PDE.

The source term f and Green's function G play the same role as lights and materials in Monte Carlo rendering (resp.); variance can hence be reduced via familiar importance sampling strategies—here we use multiple importance sampling to robustly sample screened Poisson equations for varying coefficients c, with area sources of varying size.
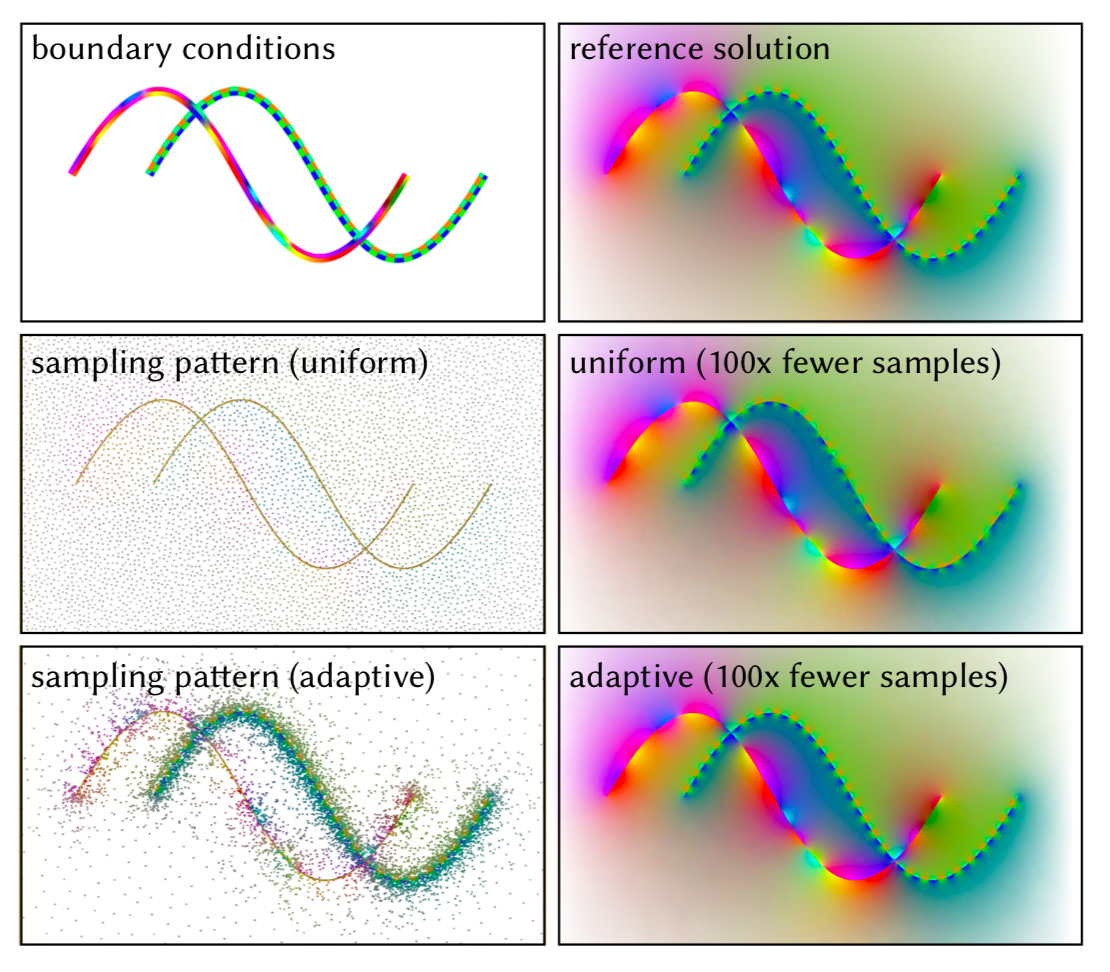
Just as mesh-based methods interpolate solution values at a few sparse points, we can rapidly visualize solutions to PDEs via scattered data interpolation. Here we solve a Laplace problem using either uniform or adaptive sampling and simple MLS interpolation to reduce the sample cost by 100x. Notice that adaptive sampling better resolves the high-frequency boundary conditions.

Bézier curves with two-sided boundary conditions plus a source term (left) define a diffusion curve image (right). Monte Carlo allows us to zoom in on a region of interest without computing any kind of global solution; since curves need not be discretized, there is no loss of fidelity.

Cross fields and corresponding quad layouts obtained by connecting singular points; no meshes were used at any stage.

We can perform shape deformation by directly editing Bézier curves, including open curves on the shape interior.

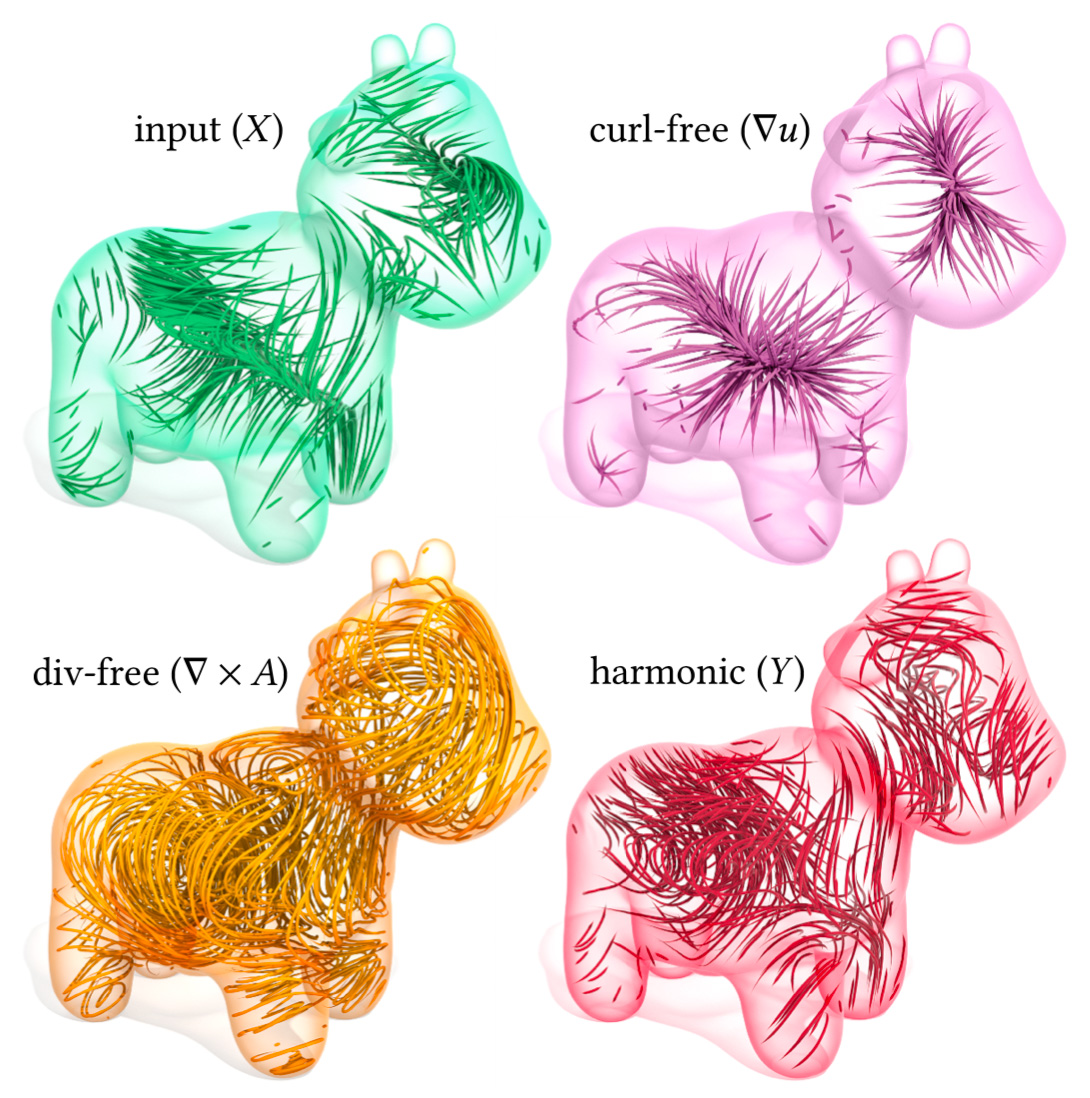
With the Monte Carlo approach, one does not even have to discretize input data. Here we decompose an input vector field X given by a closed-form, analytic expression on a domain with a Bézier boundary curve (top left) into its curl-free, divergence-free, and harmonic components.