Variational Surface Cutting
SIGGRAPH 2018 / ACM Transactions on Graphics 2018

This paper develops a global variational approach to cutting curved surfaces so that they can be flattened into the plane with low metric distortion. Such cuts are a critical component in a variety of algorithms that seek to parameterize surfaces over flat domains, or fabricate structures from flat materials. Rather than evaluate the quality of a cut solely based on properties of the curve itself (e.g., its length or curvature), we formulate a flow that directly optimizes the distortion induced by cutting and flattening. Notably, we do not have to explicitly parameterize the surface in order to evaluate the cost of a cut, but can instead integrate a simple evolution equation defined on the cut curve itself. We arrive at this flow via a novel application of shape derivatives to the Yamabe equation from conformal geometry. We then develop an Eulerian numerical integrator on triangulated surfaces, which does not restrict cuts to mesh edges and can incorporate user-defined data such as importance or occlusion. The resulting cut curves can be used to drive distortion to arbitrarily low levels, and have a very different character from cuts obtained via purely discrete formulations. We briefly explore potential applications to computational design, as well as connections to space filling curves and the problem of uniform heat distribution.
@article{Sharp:2018:VSC,
author = {Sharp, Nicholas and Crane, Keenan},
title = {Variational Surface Cutting},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
Supplemental
Céa’s Method for PDE-constrained shape optimization — basic tutorial on shape derivatives.
Shape Derivatives for Variational Cutting — derivation of flows for variational surface cutting.
variational-surface-cutting—research code (C++)
Talk
Supplemental Video
Yellow Moon Gyroid — sculpture designed by Jessica Rosenkrantz and Jesse Louis-Rosenberg using (in part) variational surface cutting.
Puzzle Cell Table Lamp — also designed using variational surface cutting, available for purchase.
Thanks to the anonymous reviewers, Christian Santangelo for early discussions about conformal cutting, and Dejan Slepčev for pointers to nonlocal isoperimetric problems. This work was sponsored in part by NSF Award 1717320 and Graduate Research Fellowship Program Grants DGE 1252522 and DGE 1745016, and gifts from Autodesk Research and Adobe Research.
This material is based upon work supported by the National Science Foundation. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Figures

A variational formulation of cutting makes it easy to explore low-distortion design alternatives. Top: By adjusting parameters in our flow, we obtain designs that look like either classic panelizations for furniture (top left) or designs more reminiscent of race car seats (top right). Alternatively, we can explore how the changing geometry of a surface affects the cuts needed to easily upholster it (bottom).

Without penalizing length, a cut that seeks to minimize distortion will evolve into a curve reminiscent of space filling curves. Surface coloring indicates area distortion (here we explicitly enforce icosahedral symmetry).

Adding a penalty in visible regions causes the flow to automatically hide the cut as much as possible, while avoiding excessive distortion. Left: no penalty. Right: with penalty.

Our flow can be used in conjunction with other design tools, or to optimize existing designs. Here we use a classic volleyball pattern (left) to define our initial cut, and flow to a new design (right) that has both smaller scale distortion (hence more uniform material stress) \emph{and} smaller cut length.
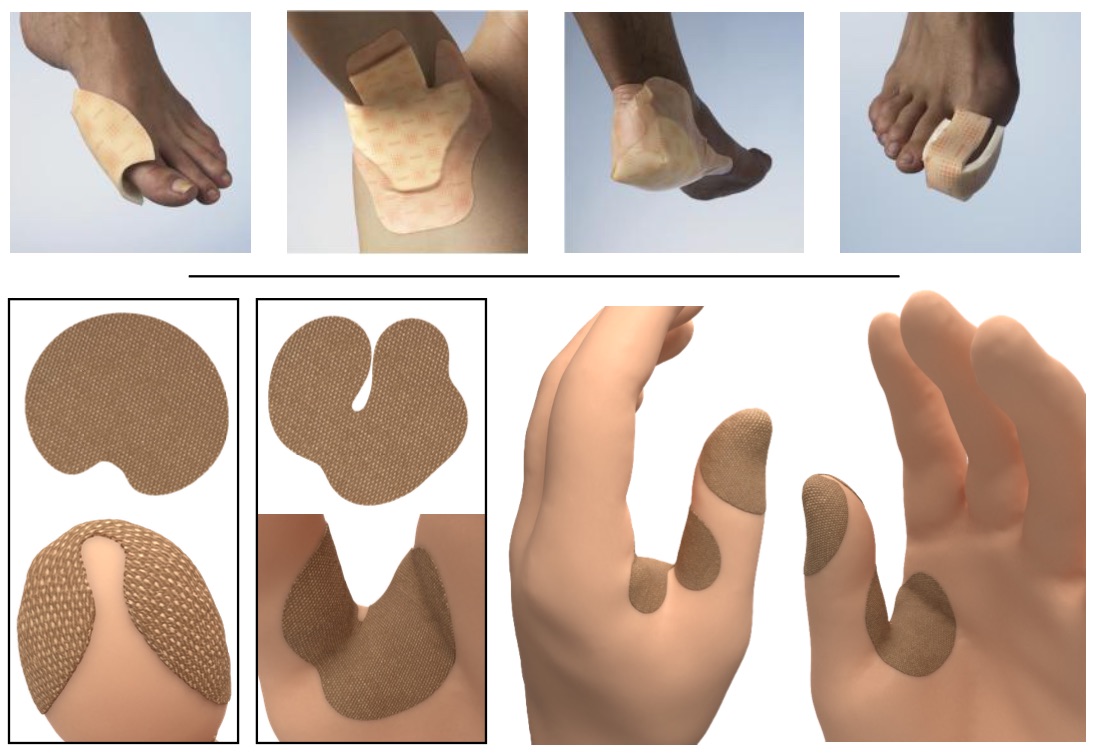
To design a small patch on the surface, we can simply penalize distortion on only one side of the cut. Here for instance, we design bandages adapted to a particular patient or wound (bottom), mimicking real medical dressings adapted to particular body parts (top, courtesy of ~\cite{fletcher2005dressings}).

To verify that we obtain near-isometric flattenings, we reconstruct a surface using the edge lengths from the 2D domain. Wrinkling and crumpling indicate excessive scale distortion (left); similar behavior will occur if such a piece is fabricated from developable material. Even a moderate reduction in distortion can significantly improve manufacturability (right).

Though not the primary focus of this work, our flow yields a low-distortion texture atlas when strong length regularization is used. Top: uniform checkerboards indicate near-isometric flattening. Bottom: flattened patches. All three examples used identical parameters; feature alignment emerges naturally, even without an explicit alignment term. (Orange indicates cuts added as a post-process, in order to obtain disk topology.)

Left: under a conformal cut flow, curves develop more oscillations in regions of high curvature, where the surface is hard to flatten. Right: since long cuts almost completely eliminate area distortion, the surface can be well-approximated by cutting the flattened shape from a sheet of inextensible material. To get a sense of approximation error, we here compute a 3D embedding with edge lengths that closely match the flattened mesh.
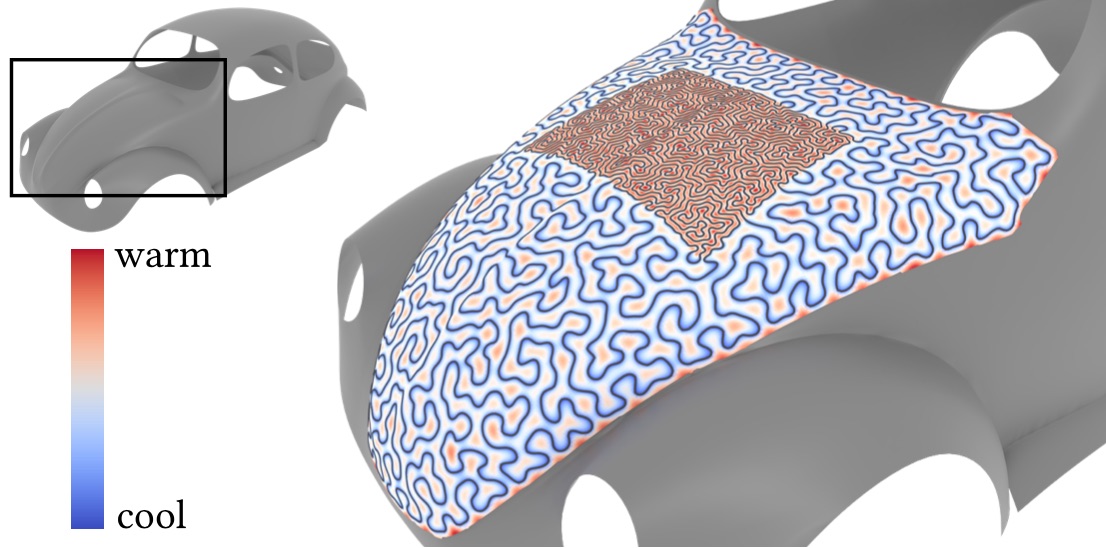
We can also find space-filling curves of variable density. Here we adapt our flow to design a cooling element on the hood of a car, where an engine block generates 10x more heat than the rest of the hood. Colors indicate steady-state temperature.
