Stripe Patterns on Surfaces
SIGGRAPH 2015 / ACM Transactions on Graphics 2015

Stripe patterns are ubiquitous in nature, describing macroscopic phenomena such as stripes on plants and animals, down to material impurities on the atomic scale. We propose an algorithm for synthesizing stripe patterns on triangulated surfaces, where branch points are automatically inserted in order to achieve user-specified orientation and line spacing. Patterns are characterized as global minimizers of a simple convex-quadratic energy which is well-defined in the smooth setting. Computation amounts to finding the smallest eigenvector of a symmetric positive-definite matrix with the same sparsity pattern as the standard graph Laplacian. The resulting patterns are globally continuous, and can be applied to a variety of tasks in design and texture synthesis.
@article{Knoppel:2015:SPS,
author = {Kn\"{o}ppel, Felix and Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Stripe Patterns on Surfaces},
journal = {ACM Trans. Graph.},
volume = {34},
issue = {4},
year = {2015},
publisher = {ACM},
address = {New York, NY, USA},
}
| GeometryCentral— | C++ implementation in the general-purpose GeometryCentral library, thanks to David Jourdan. Also includes extraction of curves along stripe patterns (including careful handling of singularities), output as a 3D polyline. |
| stripes— | C++ reference implementation. Automatically generates a stripe pattern on a given triangle mesh, with optional editing of input singularities. Also includes variants of our algorithms for provably optimal direction field generation and singularity editing, which are used to generate the input field. Depends on SuiteSparse for numerical linear algebra, and OpenGL/GLUT for visualization. |
| StripePatterns— | Mac OS X executable. (Just a compiled version of the code above!) |
Video
High-Res Images
 |
One of our results was featured on the cover of the SIGGRAPH proceedings (left)—here's the cover image and some additional figures in high-resolution (2880x1800): Photo of real mug (left) courtesy DJ Crane. The “Blub” model can be downloaded from the 3D Model Repository. |
This work was supported by the DFG Collaborative Research Center TRR 109, “Discretization in Geometry and Dynamics,” an NSF Mathematical Sciences Postdoctoral Research Fellowship (Award #1304254), and Intel. Meshes in Figs. 2, 14, 18, 22 are courtesy the Stanford Computer Graphics Lab; in Figs. 5, 15, 16, 17 courtesy AIM@Shape; and in Fig. 21 courtesy Martin Newell.
This material is based upon work supported by the National Science Foundation under Grant Number 1304254. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Figures

An arbitrary user-specified (or automatically-generated) vector field (left) drives stripe orientation and spacing (right); there are no special conditions on the input.
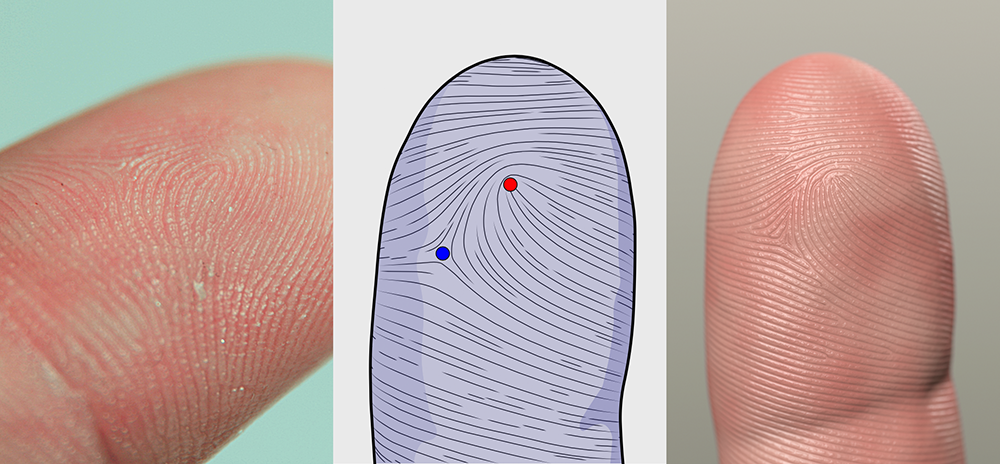
We can mimic real fingerprints (left) by using a field with prescribed singularities (center) to guide our stripe pattern (right).

Randomly perturbing a constant vector field yields a pattern reminiscent of real aeolian wind ripples (inset), here rendered as a displacement map over a flat plane.

Two orthogonal stripe patterns (red and blue) are computed separately and combined to drive a displacement map with bilateral symmetry across both axes.

Left: Photograph of a real mug with uniform, branching stripes. Right: Virtual mug synthesized using our method.

Stripe patterns can also be used to achieve a variety of artistic effects, here inspired by the work of M.C. Escher.

Due to the elliptic nature of our problem, the method is robust to noise, holes, and other severe errors in the input.

Piecewise linear interpolation (left) is substantially improved (middle) by using a closed-form, nonlinear interpolant (right).
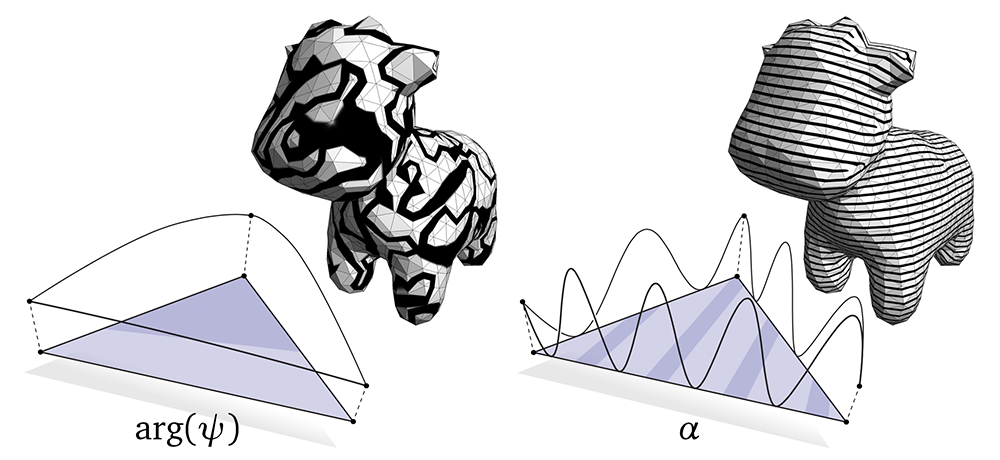
Left: for coarse meshes or high frequency stripes, naïve interpolation of angles leads to severe aliasing. Right: by carefully augmenting interpolation, we can render stripes far above the resolution of the mesh.

Our method handles line spacing that varies spatially (left), even if the target spacing function is discontinuous (right).
