Trivial Connections on Discrete Surfaces
SGP 2010 / Computer Graphics Forum
Best Paper Award

This paper presents a straightforward algorithm for constructing connections on surfaces that are as smooth as possible everywhere but on a prescribed set of isolated singularities with given index. Such connections can be used to design rotationally symmetric direction fields, which are essential in applications such as quadrilateral remeshing and texture synthesis. We compute connections by solving a single sparse linear system built from standard operators. Our solutions are globally optimal in the sense that they describe the trivial connection closest to Levi-Civita among all connections with the prescribed set of singularities. Relative to previous methods our algorithm is surprisingly simple, and can be implemented using standard operations from mesh processing and linear algebra.
Video
Supplemental
Errata (last updated: February 2013)
A Simplified Algorithm for Simply-Connected Surfaces
This brief note describes a specialization of our algorithm that makes it even easier to compute trivial connections on simply-connected surfaces (i.e., topological disks and spheres)—in this case the solution can be computed by solving a standard positive-semidefinite Poisson equation.
Adding Soft Constraints
This note describes how to add soft constraints (i.e., a guidance vector field that should be approximately followed by the solution). Interestingly enough, the problem gets no harder when adding these constraints (still just a linear solve).
Presentation
Meshes are courtesy of the AIM@Shape Project, the Stanford 3D Scanning Repository, Jotero GbR, and Hugues Hoppe. Thanks to Felix Kälberer, Matthias Nieser, and Konrad Polthier for parameterizing the Aphrodite model using QuadCover. This research was partially funded by NSF grants (CCF-0635112, CCF-0811373, CMMI-0757106, and CCF-1011944), the Center for the Mathematics of Information at Caltech, and the IAS at TU München.
|
Example direction fields. Renderings courtesy of Mehta et al.
|

Wavefront OBJ, 7.5MB
|
@article{Crane:2010:TCD,
author={Keenan Crane and Mathieu Desbrun and Peter Schr\"{o}der},
title={Trivial Connections on Discrete Surfaces},
journal={Computer Graphics Forum (SGP)},
volume={29},
number={5},
pages={1525-1533},
year={2010}
}
Source
Executable
| C++— | optimized command-line version. |
| MATLAB— | pedagogical implementation in MATLAB/GNU Octave. For simplicity, this version of the code works only on topological spheres. |
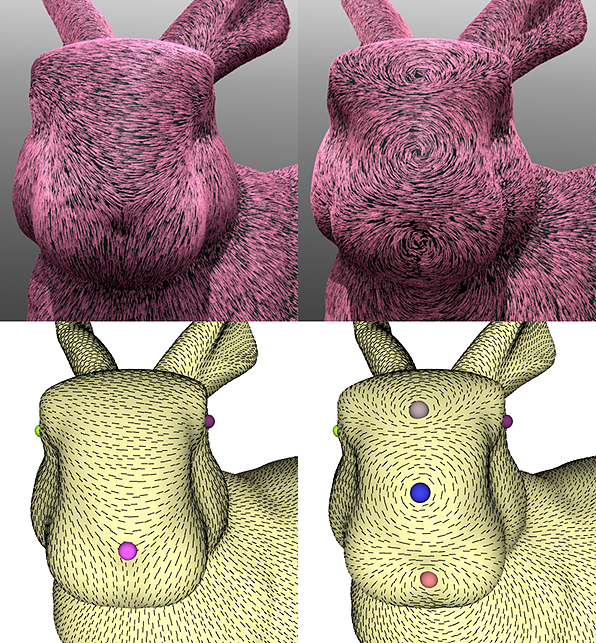
| Comb— | requires Mac OS X v10.6 or greater. Comb is a general-purpose direction field design application for Mac OS X, based on the algorithm for computing trivial connections described in our paper. Its main function is to rapidly generate smooth direction fields that satisfy some set of user-specified constraints—in particular, the user can place a set of singularities that influence field behavior. Direction fields of this type can be used for a wide variety of applications, including hair modeling, anisotropic shading, texture synthesis, and remeshing. The program takes a mesh file as input, allows a user to interactively design a direction field, and exports this field to a floating-point texture map or one of several common mesh formats. (Comb also includes rudimentary visualization tools which may be suitable for simple visualization applications.) Direction fields exported from Comb can easily be used in popular 3D modeling/rendering packages—for instance, images below show how direction fields can be used to control fur direction in Luxology's modo. |
Figures

Fields produced by our method have singularities precisely where desired (left) and nowhere else (right).
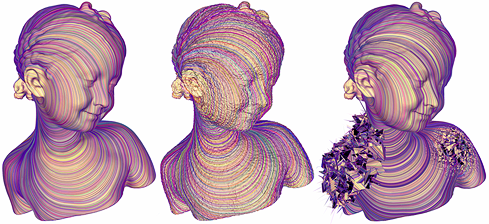
Our method is robust to noise and extreme perversions of the input, a consequence of the intrinsic, variational nature of our formulation.

Left: direction fields on moderately sized meshes can be edited in real time (~20 fps for a mesh of 20k faces). Right: even very large meshes (here ~400k faces) can be edited in about a second on a standard laptop.

The fields we generate can be used as input to quadrilateral remeshing algorithms such as QuadCover -- exact matchings are provided by our discrete connection, even around singularities.
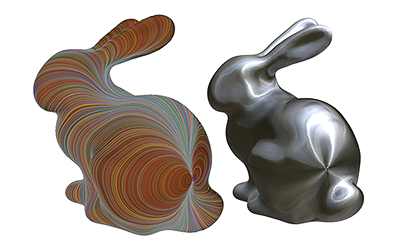
Direction fields designed using our method (left) can also be used to control the behavior of anisotropic shading (right).
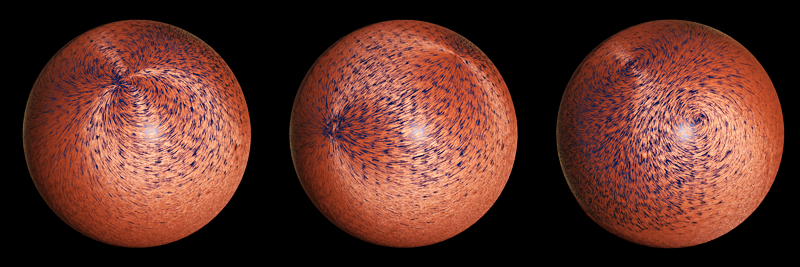
Fur example created in Comb and rendered in modo.
Fur example created in Comb and rendered in modo.
