Globally Optimal Direction Fields
SIGGRAPH 2013 / ACM Transactions on Graphics 2013
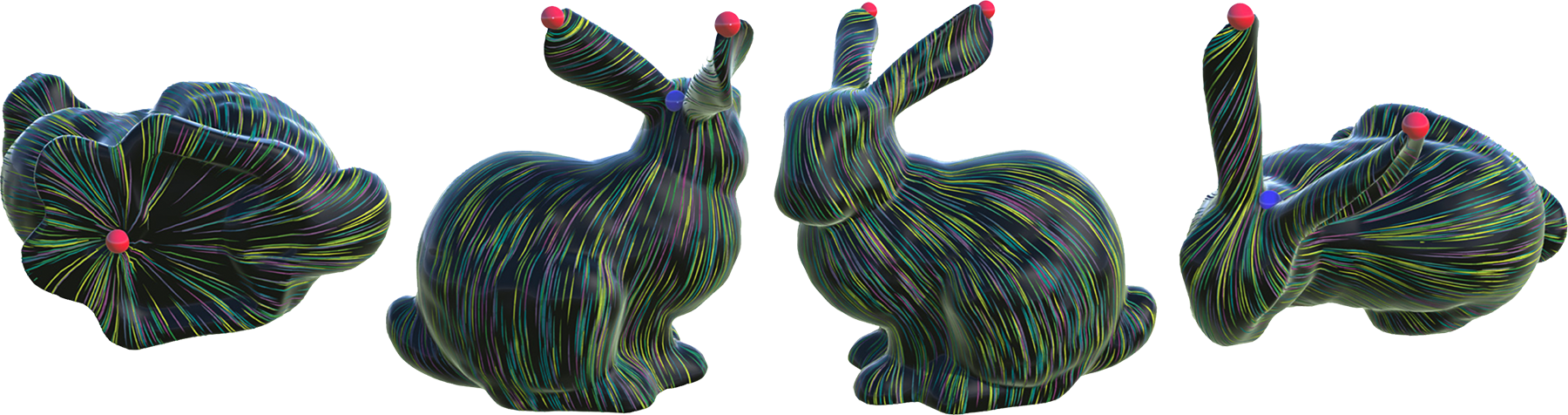
This paper presents a method for constructing smooth unit n-direction fields (line fields, cross fields, etc.) on surfaces that is an order of magnitude faster than state-of-the-art methods, while still producing fields of equal or better quality. The method is based on a simple quadratic energy whose minimizers are globally optimal in the sense that they produce the smoothest fields over all possible configurations of singularities (number, location, and index). The method is fully automatic and can optionally produce fields aligned with a given guidance field, for example, principal curvature directions. Computationally the smoothest field is found via a sparse eigenvalue problem involving a matrix similar to the cotan-Laplacian. When a guidance field is present, finding the optimal field amounts to solving a single linear Poisson problem.
Presentation
This research was supported by a Google PhD Fellowship, the Hausdorff Research Institute for Mathematics, BMBF Research Project GEOMEC, SFB / Transregio 109 “Discretization in Geometry and Dynamics,” and the TU München Institute for Advanced Study, funded by the German Excellence Initiative. Meshes provided by the Stanford Computer Graphics Laboratory and the AIM@SHAPE Shape Repository.
@article{Knoppel:2013:GOD,
author = {Kn\"{o}ppel, Felix and Crane, Keenan and Pinkall, Ulrich and Schr\"{o}der, Peter},
title = {Globally optimal direction fields},
journal = {ACM Trans. Graph.},
volume = {32},
number = {4},
year = {2013},
publisher = {ACM},
address = {New York, NY, USA},
}
- fieldgen—C++ implementation and simple interactive viewer. This version is the only one to date that supports some of the more sophisticated features described in the paper, such as the holomorphic/anti-holomorphic energy and the full finite element version of the connection Laplacian. It also supports Dirichlet boundary conditions (not described in the paper), which align the field to the shape of the domain boundary.
- Geometry-Central—C++ implementation and sophisticated interactive visualization via Polyscope. This implementation is part of a larger geometry processing library; it supports both smoothest and curvature-aligned fields, plus boundary alignment constraints.
- Directional—header-only C++ implementation, built on top of libigl and Eigen. This version is part of a larger library of direction field algorithms; note that it does not support some of the more advanced features mentioned above.
Additional Figures

The number of singularities in a field is a poor measure of its overall quality, since singularities help to provide smoothness. For instance, every surface admits a field with only one singularity—but even the smoothest such field will be extremely distorted. (This example was constructed via the trivial connections algorithm.)
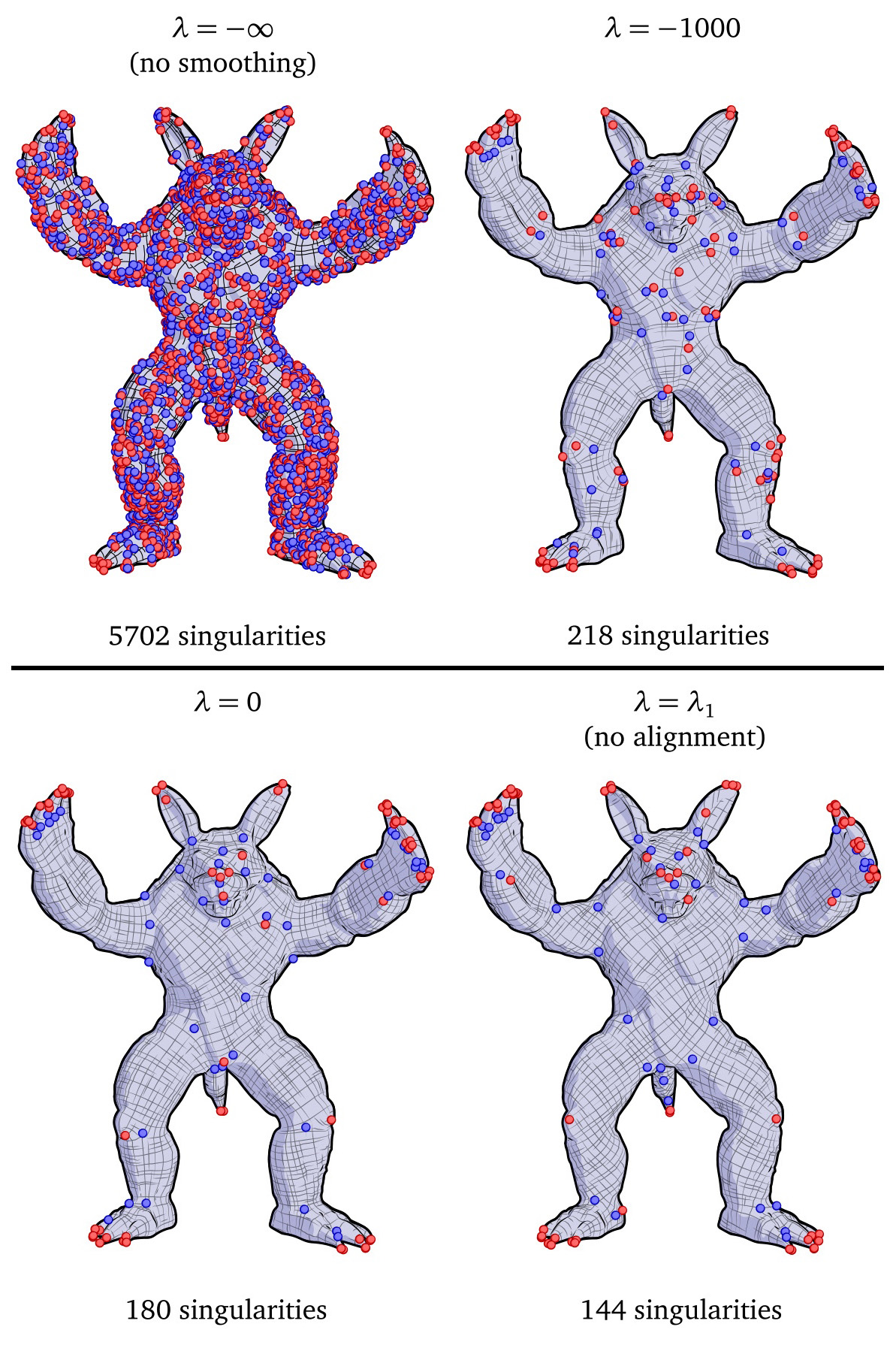
In our algorithm, a single parameter controls the trade-off between field smoothness and number of singularities.

By fixing the boundary values to the unit tangent directions and minimizing the vector Dirichlet energy, we obtain fields that are nicely adapted to the shape of the domain. (These boundary conditions are not described in the paper, but are implemented in the standard way: remove rows/columns of the Laplace matrix corresponding to boundary vertices, and move the corresponding values to the right-hand side; energy minimization then corresponds to solving a Laplace equation.)

Alternative visualization of example from Figure 10, with and without singularities. Full size version here.
