Symmetric Moving Frames
SIGGRAPH 2019 / ACM Transactions on Graphics 2019

A basic challenge in field-guided hexahedral meshing is to find a spatially-varying frame that is adapted to the domain geometry and is continuous up to symmetries of the cube. We introduce a fundamentally new representation of such 3D cross fields based on Cartan's method of moving frames. Our key observation is that cross fields and ordinary frame fields are locally characterized by identical conditions on their Darboux derivative. Hence, by using derivatives as the principal representation (and only later recovering the field itself), one avoids the need to explicitly account for symmetry during optimization. At the discrete level, derivatives are encoded by skew-symmetric matrices associated with the edges of a tetrahedral mesh; these matrices encode arbitrarily large rotations along each edge, and can robustly capture singular behavior even on coarse meshes. We apply this representation to compute 3D cross fields that are as smooth as possible everywhere but on a prescribed network of singular curves—since these fields are adapted to curve tangents, they can be directly used as input for field-guided mesh generation algorithms. Optimization amounts to an easy nonlinear least squares problem that behaves like a convex program in the sense that it always appears to produce the same result, independent of initialization. We study the numerical behavior of this procedure, and perform some preliminary experiments with mesh generation.
Teaser Video
Thanks to Heng Liu and David Bommes for help generating mesh examples, and to the anonymous reviewers for useful feedback. This work was supported by a Packard Fellowship, NSF Award 1717320, and gifts from Autodesk, Adobe, and Facebook.
Trivial Connections on Discrete Surfaces - provides a gentler (2D) introduction to some of the key ideas used in this paper.
@article{Corman:2019:SMF,
author = {Etienne Corman and Keenan Crane},
title = {Symmetric Moving Frames},
journal = {ACM Trans. Graph.},
volume = {38},
number = {4},
year = {2019},
publisher = {ACM},
address = {New York, NY, USA},
}
|
A few example hex meshes. Files can easily be viewed in the browser via hexalab.net. Thanks to Heng Liu and David Bommes for help with parameterization and mesh extraction.
|
VTK, 1.4MB
|
Figures

Within small neighborhoods, a 2D or 3D cross field can be represented by an ordinary frame field. Its derivatives ω therefore obey standard structure equations, which provide the basic constraints for our method.

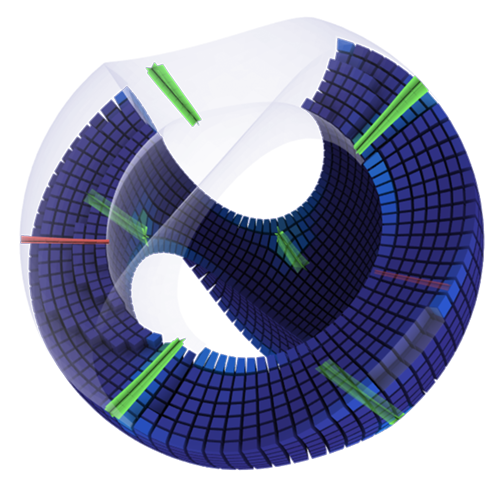
Some fields computed via our method; for each model we show the input network (blue), Darboux derivative ω (white) and 3D cross field (black).

Hexahedral meshes generated from our fields; for each mesh we show a “fallaway” view to visualize interior element quality. Even coarse meshes (top row) respect the given singularity structure, and generally exhibit good element quality.
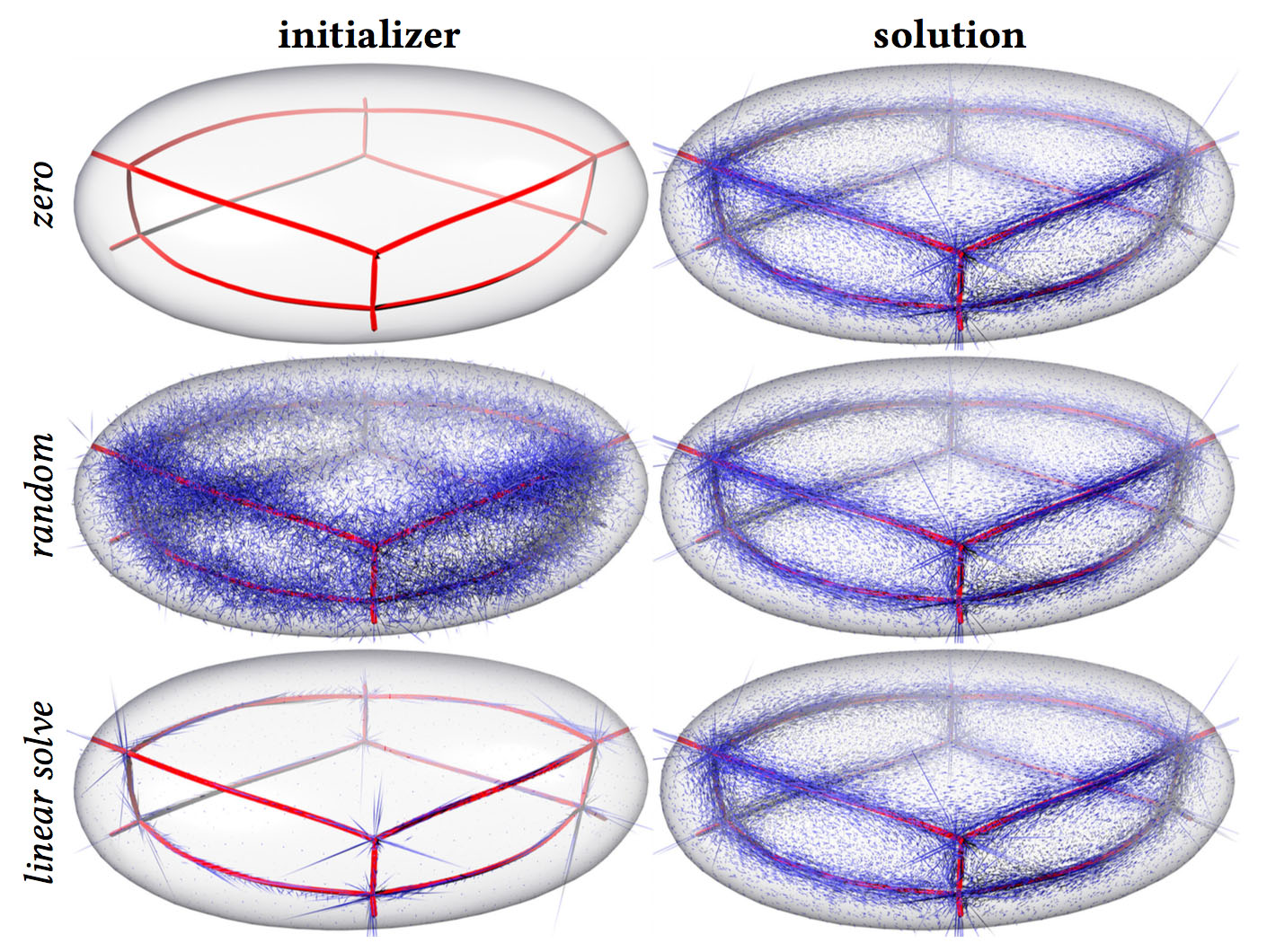
Independent of initial guess (left), our optimization problem yields an identical solution (right) up to floating point error. Here we plot ω as a vector per edge.
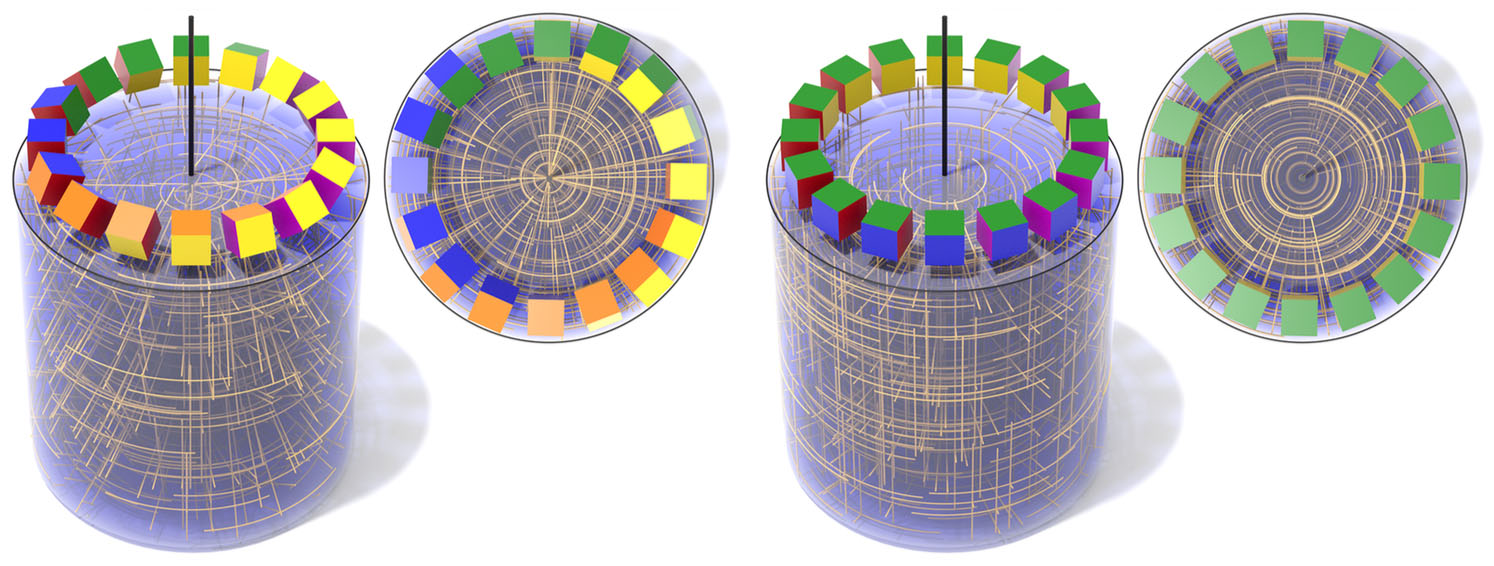
Control over the behavior of singularities is essential, since even extremely smooth fields (left) may not be meshable. Using symmetric moving frames, we can ensure that one frame axis is always tangent to a given singular curve (right), without having to determine this axis a priori.
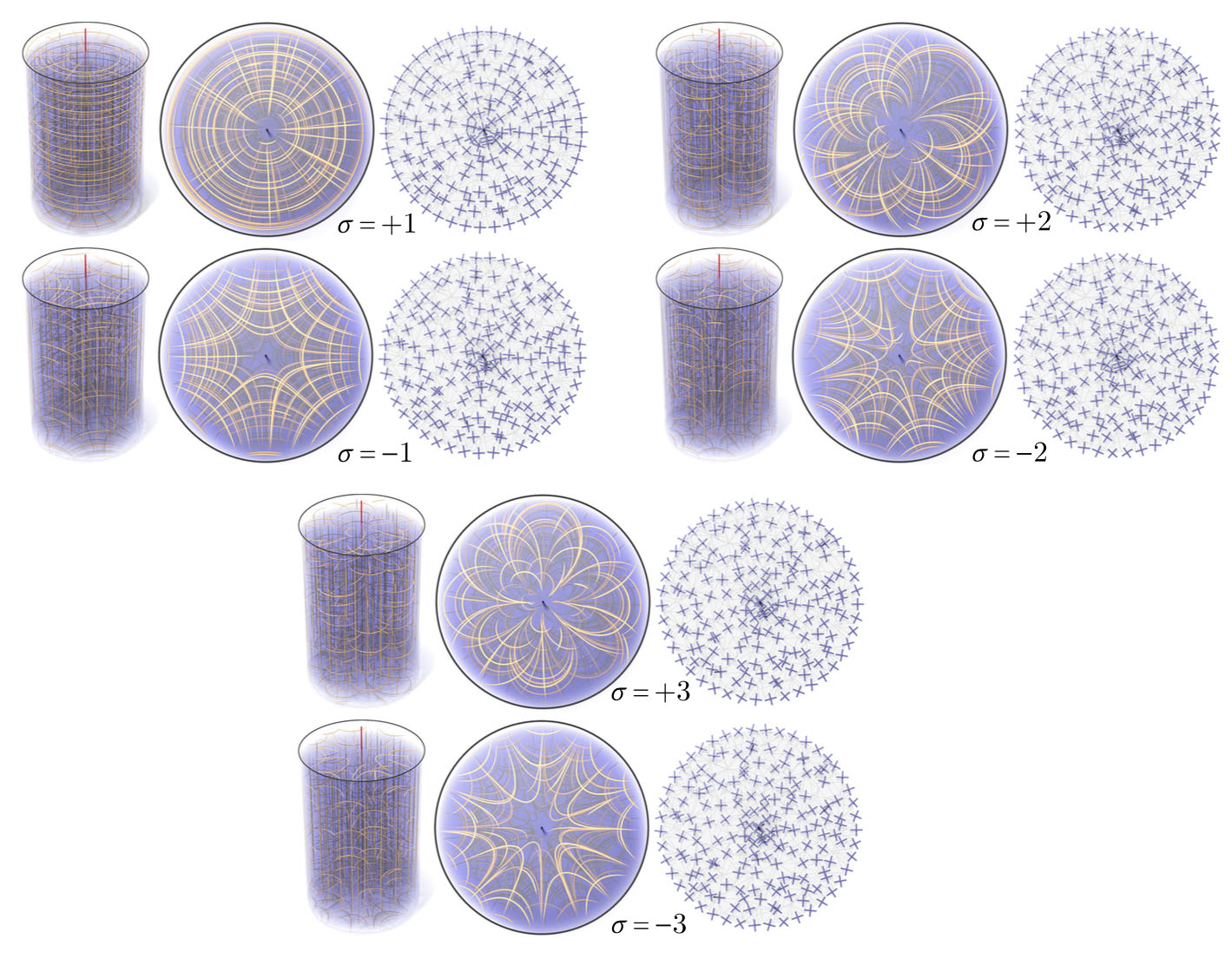
The index σ determines how many times the field winds around a singular curve. Since we directly encode the angular change along each edge, we can robustly handle large rotations even on very coarse meshes.
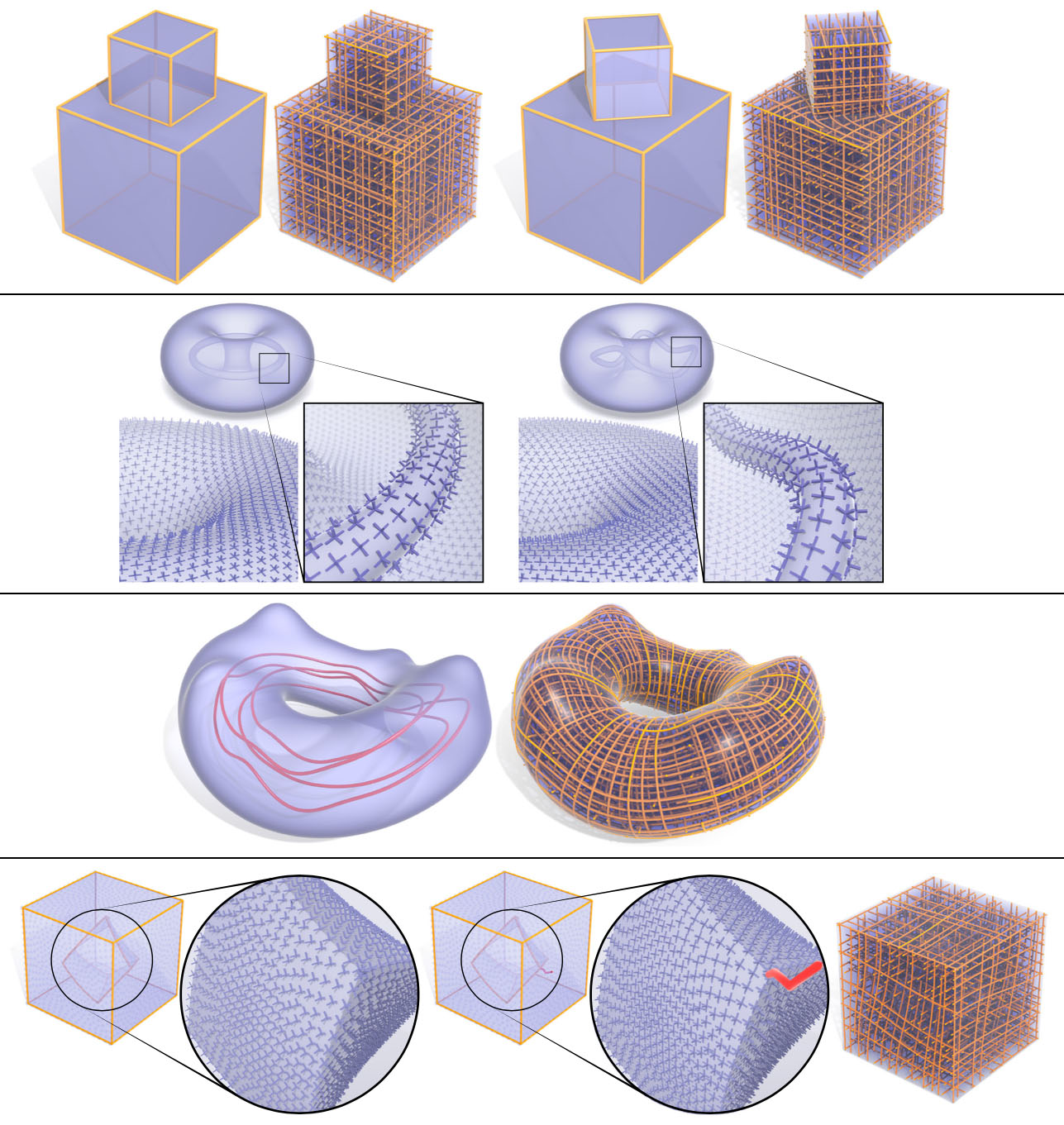
Even when the constraint set has disconnected components, integrability of ω is typically sufficient to ensure that the frame is correctly adapted to boundary normals and curve tangents—even in the absence of symmetry. Here we show a domain with disconnected feature curves (top), disconnected boundary components (middle top), and singular loops that make no contact with the boundary (middle bottom). A rare exception is shown in (bottom), where the cross field on two nested cubes can be globally represented by an ordinary rotation field; here we can simply connect components by a feature curve (in red) to ensure proper alignment.

We can allow the torsion of the frame along singular and feature curves to be free during optimization—and hence do not have to determine torsional periods a priori. Here for instance the frame automatically makes the correct number of twists as it travels around the red loop (from le to right: 0, 1, and 2), keeping it compatible with the boundary normals.
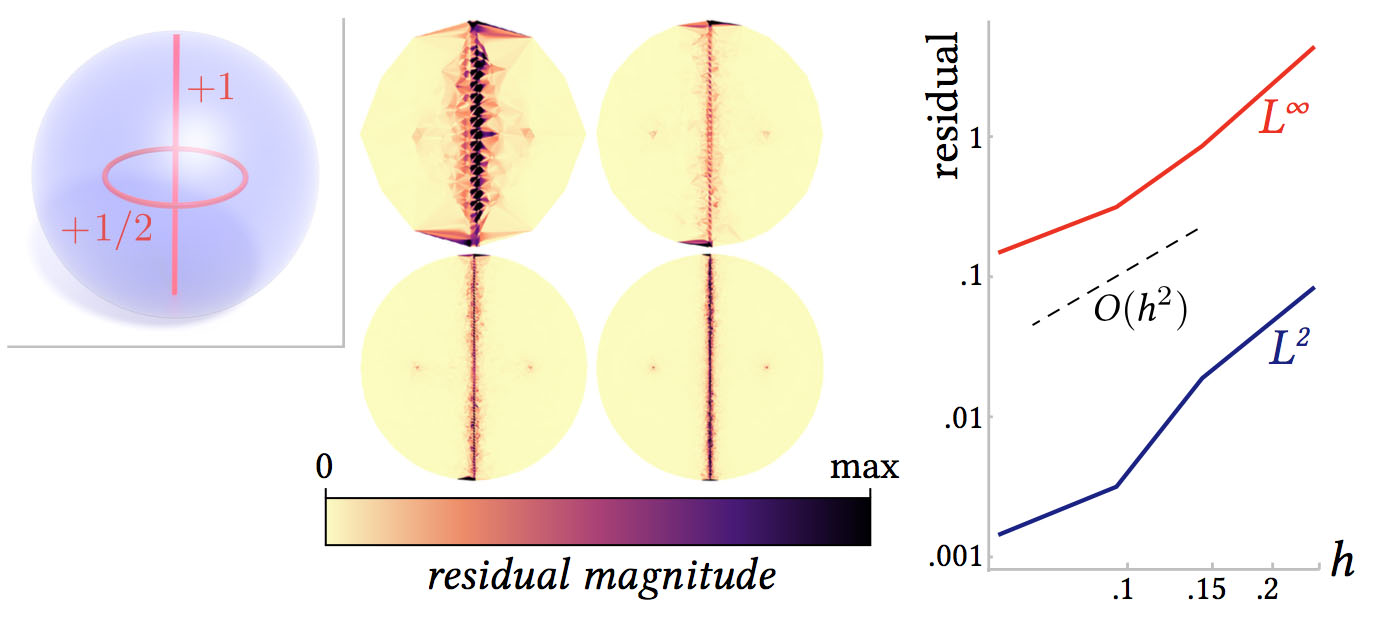
Our discretization of Cartan’s structure equation exhibits second order convergence with respect to mean edge length h, providing good numerical behavior even on coarse models.
