A Laplacian for Nonmanifold Triangle Meshes
Symposium on Geometry Processing 2020
Best Paper Award

We describe a discrete Laplacian suitable for any triangle mesh, including those that are nonmanifold or nonorientable (with or without boundary). Our Laplacian is a robust drop-in replacement for the usual cotan matrix, and is guaranteed to have nonnegative edge weights on both interior and boundary edges, even for extremely poor-quality meshes. The key idea is to build what we call a “tufted cover” over the input domain, which has nonmanifold vertices but manifold edges. Since all edges are manifold, we can flip to an intrinsic Delaunay triangulation; our Laplacian is then the cotan Laplacian of this new triangulation. This construction also provides a high-quality point cloud Laplacian, via a nonmanifold triangulation of the point set. We validate our Laplacian on a variety of challenging examples (including all models from Thingi10k), and a variety of standard tasks including geodesic distance computation, surface deformation, parameterization, and computing minimal surfaces.
Presentation
Nonmanifold Laplacians in Physical Simulation - In our paper, we neglected to reference papers from mesh-based physical simulation that build a discrete Laplace operator for simulation of, e.g., soap foams, which necessarily exhibit nonmanifold features. For instance: Da et al 2015, Ishida et al 2017, and Ishida et al 2020. The Laplacian used by these methods is equivalent to taking the sum of per-triangle cotan Laplacians, without performing any intrinsic edge flips. The key difference is that our Laplacian satisfies the intrinsic Delaunay property, and hence exhibits a discrete maximum principle as well as (empirically) better numerical robustness on low-quality meshes. Hence, our comparisons with the “(standard) cotan Laplacian” give a good idea of how our “tufted Laplacian” (which makes use of the intrinsic Delaunay triangulation) will generally behave compared to the Laplacian defined in these physics simulation papers.
nonmanifold-laplacian—C++ implementation; given any triangle mesh mesh, dumps a high-quality Laplacian to disk. Also includes an interactive visualization via Polyscope).
Thanks to Boris Springborn and Max Wardetzky for helpful discussions. This work was supported by NSF award 1943123, an NSF Graduate Fellowship, a Packard Fellowship, and gifts from Autodesk, Adobe, Activision Blizzard, Disney, and Facebook. Thanks to creators of meshes: Thingiverse user Ramenspork’s high school students and TurboSquid user Gatzegar.
@article{Sharp:2020:LNT,
author={Nicholas Sharp and Keenan Crane},
title={{A Laplacian for Nonmanifold Triangle Meshes}},
journal={Computer Graphics Forum (SGP)},
volume={39},
number={5},
year={2020}
}
Figures
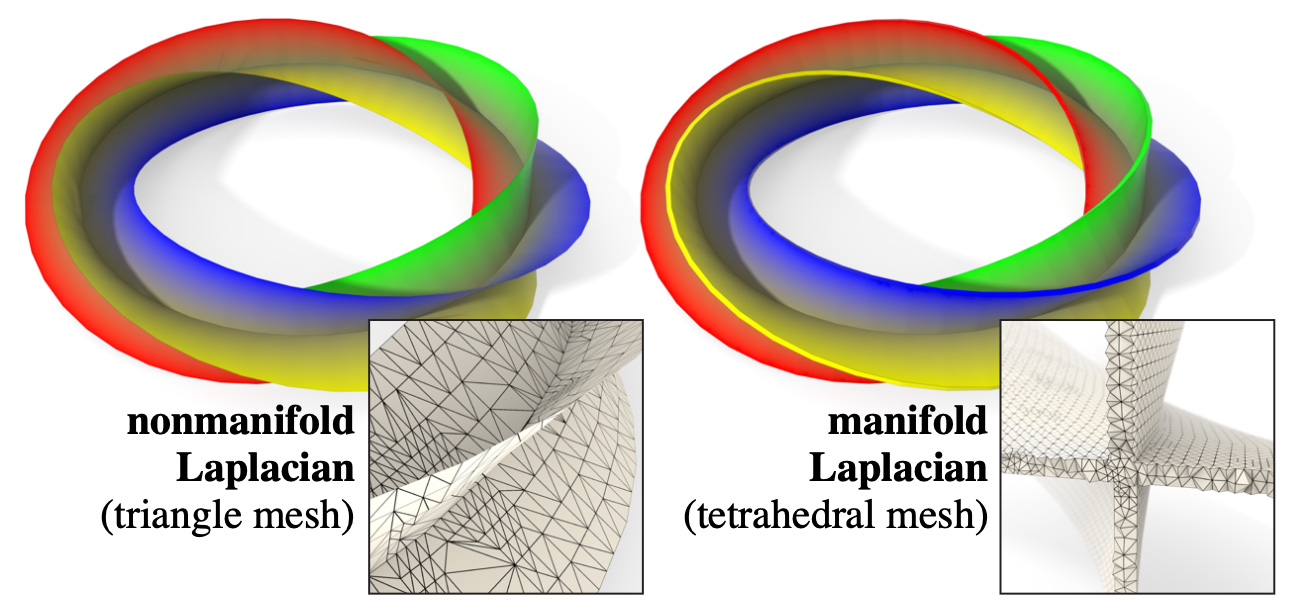
We define a Laplacian for nonmanifold triangle meshes, which generally behaves like the Laplacian on a slightly thickened domain. Here for instance we get a near-identical harmonic interpolation of boundary values using our Laplacian on a triangle mesh (left) or with the standard Laplacian on a tetrahedral mesh (right).

We also define a new point cloud Laplacian, which inherits the same basic properties of our mesh-based Laplacian—enabling many algorithms to be reliably implemented on point clouds. Here we plot the angular component θ of the logarithmic map, which provides a global surface parameterization around a given point.

Even for poor-quality nonmanifold meshes, we achieve the Delaunay criterion everywhere (thereby avoiding negative weights)—without inserting new vertices.
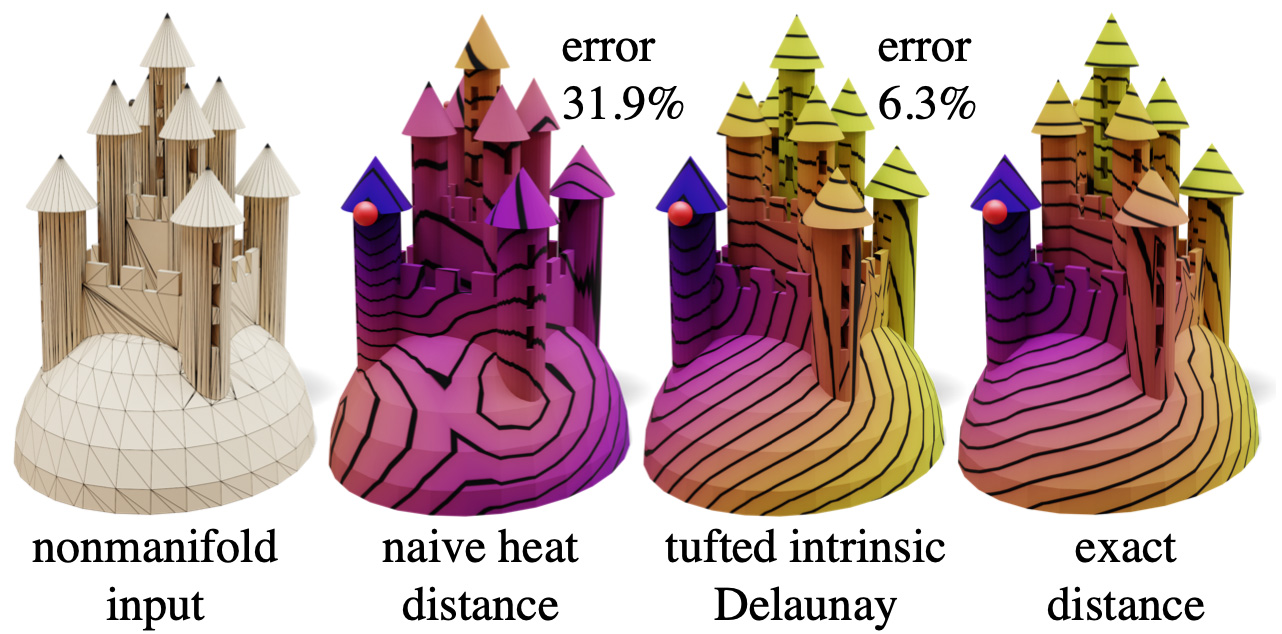
Our Laplacian greatly improves the accuracy of PDE-based algorithms on poorly tessellated nonmanifold meshes. Here, we compute geodesic distance via the heat method, which yields large error with the cotan Laplacian. Substituting our tufted Laplacian brings the result much closer to the exact solution.

A poor-quality nonmanifold mesh resulting from a boolean operation (bottom left) deformed in the spirit of Lipman et al [2004]. The standard cotan Laplacian yields nonsensical numerical output, whereas our Laplacian produces the expected deformation.

Left: Our Laplacian yields the correct geometry for nonmanifold minimal surfaces, even on near-degenerate meshes. Right: For a high-quality mesh, the ordinary cotan-Laplacian may still fail to exhibit the maximum principle, producing vertices that are not in the convex hull of their neighbors (as shown here), or flipped triangles whose normals differ from their neighbors by more than 90°.

Unlike previous discrete Laplacians, ours is guaranteed to have nonnegative edge weights even at the domain boundary. Here, harmonic interpolation of a set of pinned values stays inside the given range. In contrast, even the intrinsic Laplacian (as well as ordinary cotan-Laplace) yields values far outside this range.

Harmonic Green's function on a point cloud. Here, standard Gaussian weights à la Belkin et al. [2008] (left) can yield numerical underflow for time steps h that are small enough to resolve the solution. Using Delaunay triangulations to determine connectivity à la Clarenz et al. [2004] (center) is more stable, but can still yield erroneous negative values. Our tufted point cloud Laplacian (right) guarantees a discrete maximum principle, yielding an accurate result.
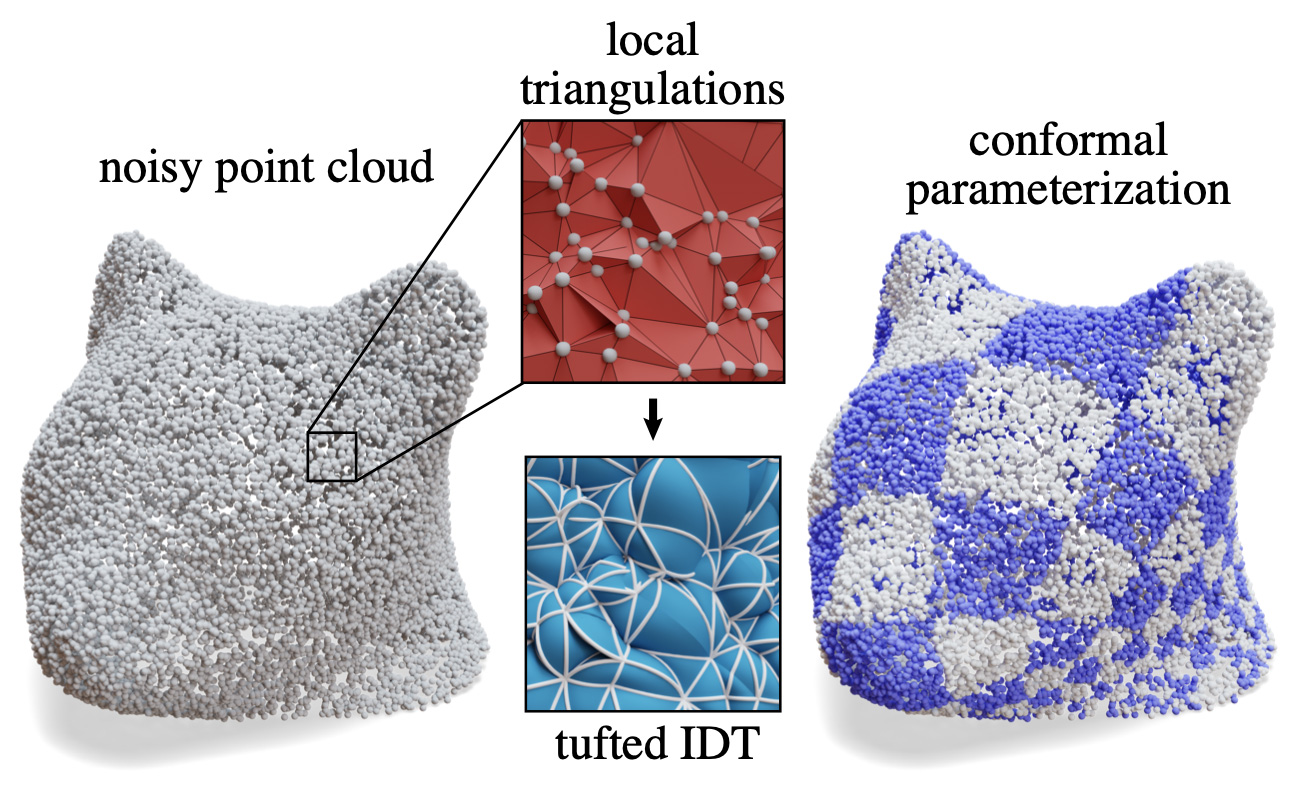
To construct a high-quality point cloud Laplacian, we take the union of local triangulations about each point, resulting in a nonmanifold mesh on which we construct our tufted Laplacian. Here, we use this Laplacian to compute the spectral conformal parameterization of a surface.
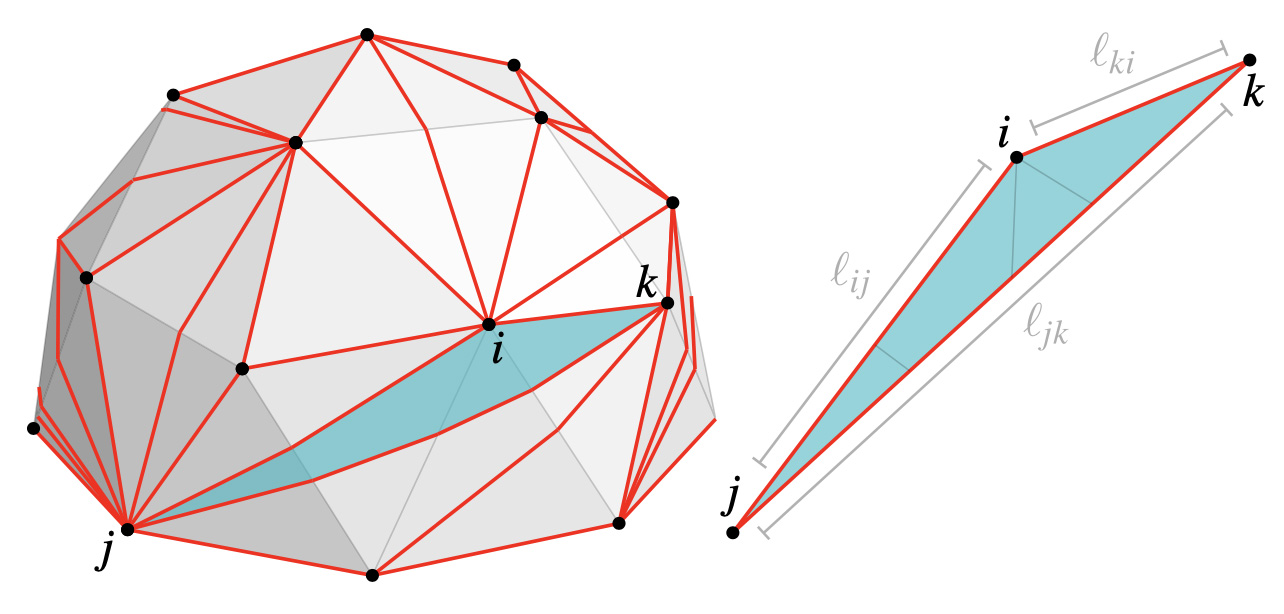
Left: Much as a planar point set can be triangulated in many different ways, an intrinsic triangulation allows the vertices of a polyhedron to be connected by many different straight (geodesic) edges along the surface. Right: Each intrinsic triangle can be flattened into the plane without distortion; its geometry (area, angles, etc.) is hence completely described by just three edge lengths.
