Developability of Triangle Meshes
SIGGRAPH 2018 / ACM Transactions on Graphics 2018

Developable surfaces are those that can be made by smoothly bending flat pieces without stretching or shearing. We introduce a definition of developability for triangle meshes which exactly captures two key properties of smooth developable surfaces, namely flattenability and presence of straight ruling lines. This definition provides a starting point for algorithms in developable surface modeling—we consider a variational approach that drives a given mesh toward developable pieces separated by regular seam curves. Computation amounts to gradient descent on an energy with support in the vertex star, without the need to explicitly cluster patches or identify seams. We briefly explore applications to developable design and manufacturing.
Video
Presentation
Thanks to Timothy Sun for preliminary discussion and investigation, and to Ryan Schmidt for performing the toolpath extraction and milling in Faucet. This work was sponsored in part by NSF Awards 1717320 1409286, 1717268, and 1319483, and gifts from Adobe, Autodesk Research, Pixar, and SideFX Software.
@article{Stein:2018:DSF,
author = {Oded Stein and Eitan Grinspun and Keenan Crane},
title = {Developable Surface Flow},
journal = {ACM Trans. Graph.},
volume = {37},
number = {4},
year = {2018},
publisher = {ACM},
address = {New York, NY, USA},
}
Figures

How should one approximate a perfect sphere by developable pieces? Due to symmetry, there is no canonical “best” answer. Instead, we guide the surface toward a desired design by choosing an initial tessellation (shown at top) that breaks this symmetry.

Flattenability alone is not enough to ensure that a surface is easy to fabricate. For instance, both the crumpled piece of paper (top left) and noisy triangle mesh (bottom left) can be exactly flattened into the plane, but would be difficult to actually assemble from stiff material. In contrast, the smooth piece of paper (top right) and triangle mesh (bottom right) are both exactly flattenable and have straight ruling lines passing through each point. We seek surfaces of the latter kind.

Denoising a developable sheet (left) by simply minimizing angle defect leads to a flattenable but noisy surface (center), whereas encouraging discrete developability yields a smoother ruled surface (right).

Here we approximate a given shape (leftmost in each image) with a surface that is developable away from seam curves. Unlike methods that partition the surface into individual pieces, seams can blend organically into the design. Left to right: a swingarm model produced via topological optimization (courtesy Autodesk); the handle of a drill; and a guitar body, which naturally yields features appearing in real guitar designs (bottom right).
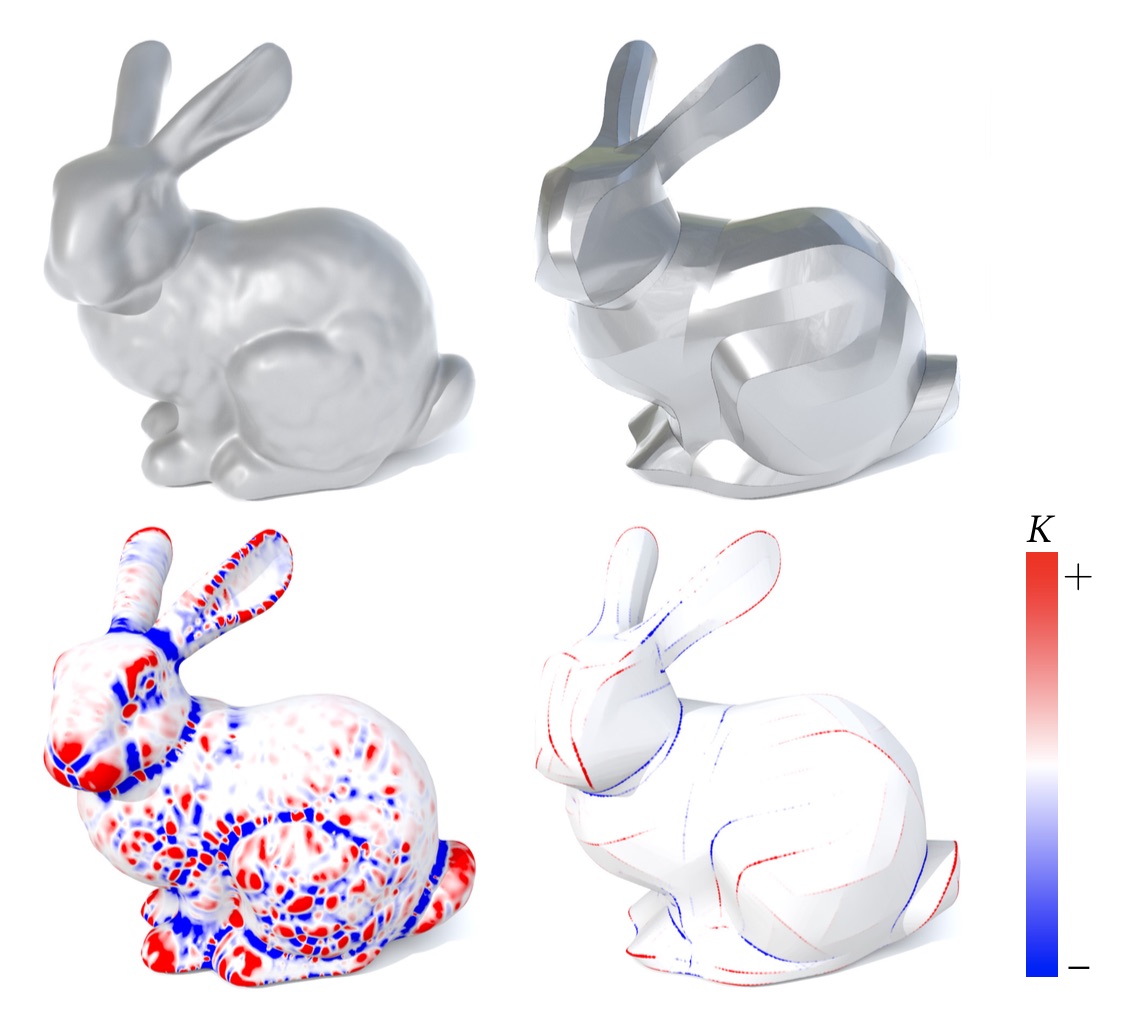
On the Stanford bunny (top row), Gaussian curvature K concentrates onto a sparse collection of curves (bottom row).

Beyond the traditional task of shape approximation, our method enables developable shape exploration by starting with a coarse mesh and optimizing/refining toward a piecewise developable surface with organic flowlines. (Input mesh in each figure is shown in wireframe.)

Simple test of physical feasibility: an initial mesh of a face (left) is optimized to obtain a piecewise developable approximation (center), which is then cut from paper, glued together, and spray painted to obtain a physical model (right).
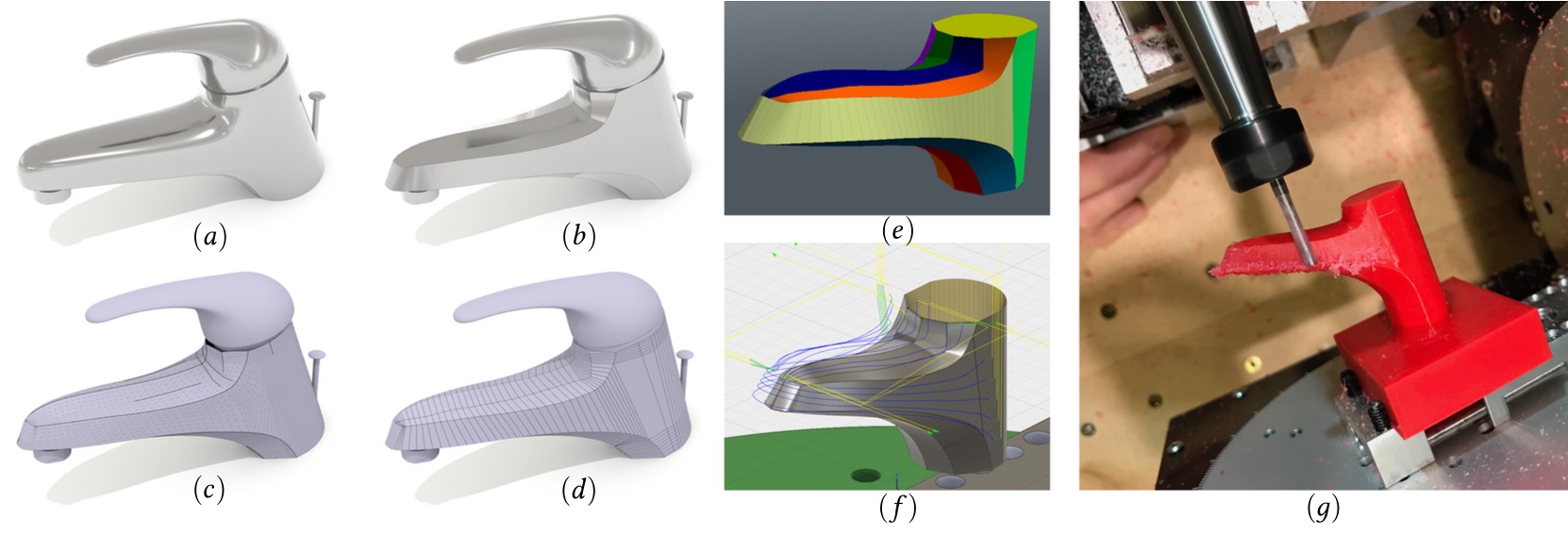
Prototype of fabrication via flank milling. An originally smooth faucet design (a) evolves into a piecewise developable surface (b) with fairly clear seam curves and ruling lines (c) which are extracted by hand (d) in a polygon mesh editor and partitioned into PQ strips (e). These strips are then semi-automatically converted into tool paths (f) via NURBS patches. A contour of the final piece is then flank milled using a hobbyist 5-axis CNC mill (g).
