Home
Research
* Principles
Motor Control
Robotics
Projects
Publications
Students
Teaching
 |
Principles of Legged Dynamic Systems |
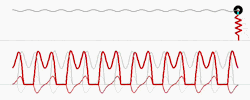
Although animals and humans represent very complex dynamic systems, they show strikingly uniform and simple dynamics at the level of the center of mass (COM) when they walk or run. The COM dynamics can be measured using ground reaction force plates that record the forces with which the legs push against the ground during stance in locomotion. The figure below shows these leg forces for walking (left) and running (right). In the vertical direction (Fy) they are characterized by an M-shape pattern for walking and a bell-shape pattern for running.
 |
Figure 1
A simple model that unites walking and running
We showed in a simulation study that these force patterns can be
explained with a simple, bipedal spring-mass model. This
model not only combines the COM dynamics observed in walking and
running in one mechanical system, but also demonstrates these
gaits to be just two out of many solutions to legged locomotion
offered by compliant leg behavior and accessed by energy or
speed. I am interested in hierarchical expansions of this
model building up a theory of legged dynamic systems.
 |
|
Figure 2
More details about this research can be found in
- H Geyer, A Seyfarth, R Blickhan. Compliant leg behaviour explains basic dynamics of walking and running. Proc R Soc B 273: 2861?2867, 2006. [PDF]
- H Geyer. Simple models of legged locomotion based on
compliant leg behavior. Ph.D. Thesis Ch 4: 49?68, 2005. [PDF]
Mathematical solutions to legged dynamics
The spring biped is perhaps the simplest model that describes walking and running dynamics. It has only three independent parameters and one can characterize and understand its behavior with brute force parameter searches (compare figure 2). However, similar searches yield less meaningful results when extending this model into more complex ones. Mathematical solutions to the model dynamics can provide a deeper understanding. And I am interested in obtaining such solutions.
This task is not trivial. The spring-mass model describes a piecewise holonomic, nonlinear dynamic system whose equations of motion cannot be solved in closed form. Assuming that gravity co-rotates with the leg axis in stance, we derived an approximate solution to the model dynamics in running that is comparably simple yet surprisingly accurate.

|
 |
Figure 3
The approximate solution can help to understand control strategies in running. For instance, we derived an explicit formula for how the leg parameters must be adjusted to use mechanical self-stability in legged systems. On the other hand, the solution provides a stepping stone toward a more general mathematical solution that includes running and walking.
More details about this research can be found in
- H Geyer, A Seyfarth, R Blickhan. Spring-mass running: simple approximate solution and application to gait stability. J Theor Biol 232: 315?328, 2005. [PDF]
- H Geyer. An approximate solution to human locomotion at the
level of the center of mass. In preparation. [Ask
me for details]
Mechanical selfstability
Because legged locomotion is a repetition of stance and swing phases, the behavior of the hybrid-dynamic spring-mass model can be investigated using Poincare map analysis. This analysis shows a remarkable result. Legged locomotion is mechanically selfstable.
Poincare map analysis is illustrated in figure 4 for
running. For each running step i, the model behavior is
uniquely characterized by the state variable `apex height'
(y_i). Mapping the change of this variable from one step (i)
to the next (i+1) identifies periodic solutions (y_i+1 = y_i =
y*). These solutions are stable if the slope of the map
stays within +/- 45 deg in the neighborhood of y*.

|
 |
Figure 4
We showed that for well-chosen model parameters (example: swing leg orientation alpha_0=67deg in figure 4), running is mechanically selfstable. Without any feedback about (small) ground disturbances, the model stabilizes into a steady state running gait. The same holds true for the bipedal spring-mass model and walking.
More details about this research can be found in
- H Geyer, A Seyfarth, R Blickhan. Natural dynamics of
spring-like running: emergence of self-stability. In 5th Int
Conf on Climbing and Walking Robots (CLAWAR), eds. P Bidaud and
FB Amar, Professional Engineering Publishing Ltd., London. pp.
87?91, 2002. [PDF]
- A Seyfarth, H Geyer, M Guenther, R Blickhan. A movement criterion for running. J Biomech 35: 649?655, 2002. [PDF]
- H Geyer, A Seyfarth, R Blickhan. Spring-mass running: simple approximate solution and application to gait stability. J Theor Biol 232: 315?328, 2005. [PDF]
- H Geyer. Simple models of legged locomotion based on compliant leg behavior. Ph.D. Thesis Ch 4: 49?68, 2005. [PDF]
Canonical expansion to selfstability control
The Poincare map analysis (figure 4) reveals a rather small tolerance of mechanical selfstability to ground disturbances and parameter adjustments. The required angular precision is about one degree. And the basin of attraction is narrow on the left side of the steady state solution y*, tolerating obstacle heights of a mere 5 percent of the leg length.
We showed that mechanical selfstability can be maximized in a canonical way. Maximum selfstability in running is equivalent to a deadbeat control that attracts any initial state y_i of the model into a desired state y_des within one step y_i+1=y_des=y*. In the language of Poincare maps this equals a horizontal map at the level y_des. Figure 5 illustrates that this imaginary return map can be realized if, for different initial apex heights y_i, different leg orientations alpha_0 in swing are selected.

|
 |
Figure 5
The relationship alpha_0(y_i) represents a control that molds the basin of attraction into a desired shape, in a canonical way. It suffers however from a serious flaw. Continuous feedback about the ground clearance of the foot point is required to adapt alpha_0 with respect to the corresponding apex height. This control neither is elegant nor does it use mechanical selfstability inherent to legged dynamics.
A unique transformation changes the situation. Since any
alpha_0 defines a landing height y_l = L_0 * sin(alpha_0), the
pair y_i and alpha_0(y_i) corresponds to a defined drop height
Dy(y_i) = y_i - y_l. And this drop height uniquely
transforms into a flight time Dt(y_i) after the apex event in
running. In reverse this means that, for every time Dt,
there is a leg orientation alpha_0(Dt) in swing, which guarantees
that if the model hits ground at that moment, it gets directed
into the desired state y_des.
 |

|
Figure 6
As a result the model rejects ground disturbances without sensing them, within one step. This result is illustrated in figure 6 in a simulation and with a spring-leg robot.
The approach generalizes to 3D locomotion. In 3D, the spring-mass model is characterized by the attack and splay angles of the leg prior to landing (alpha and beta in figure 7). Both angles can be used as control inputs to not only reject ground disturbances but also change the heading direction. As before, the resulting angle control laws can be transformed into time laws alpha(t) and beta(t) after the apex event. Without measuring ground level, the resulting control achieves defined turns in rough terrain running.
 |

|
Figure 7
More details about this research can be found in
- A Seyfarth, H Geyer. Natural control of spring-like running:
optimized self-stabilization. In 5th Int Conf on Climbing and
Walking Robots (CLAWAR), eds. P Bidaud and FB Amar, Professional
Engineering Publishing Ltd., London. pp. 81?85, 2002. [PDF]
- A Seyfarth, H Geyer, HM Herr. Swing-leg retraction: a simple
control model for stable running. J Exp Biol 205: 2547?2555,
2003. [PDF]
- HM Herr, A Seyfarth, H Geyer. Speed-adaptive control scheme for legged running robots. US Patent 7295892, 2003. [PDF]
- E Dittrich, H Geyer, A Karguth, A Seyfarth. Obstacle avoidance
in a simple hopping robot. In 9th Int Conf on Climbing and
Walking Robots (CLAWAR), Brussels, Belgium, 2006. [PDF]
- M Ernst, H Geyer, R Blickhan. Spring-legged locomotion on uneven ground: a control approach to keep the running speed constant. In 12th Int Conf on Climbing and Walking Robots (CLAWAR), eds O Tosun, HL Akin, MO Tokhi, GS Virk, ISBN 981-4291-26-9, 639?644, 2009. [PDF]
- M Ernst, H Geyer, R Blickhan. Extension and customization of self-stability control in compliant legged systems. Bioinspiration and Biomimetics, http://dx.doi.org/10.1088/1748-3182/7/4/046002, 2012. [PDF]
- A Wu, H Geyer. The 3-D spring-mass model reveals a time-based deadbeat control for highly robust running and steering in uncertain environments. IEEE Transactions on Robotics 29(5): 1114-1124, 2013. [PDF]
Application to humanoid robots
We are interested in transferring and verifying theoretical models of legged dynamics and control models on bipedal robot hardware. In particular, we own a copy of Oregon State's ATRIAS 2.1 biped robot (Figure 8). The biped has very lightweight legs, mimicking the mass distribution of the spring-mass model. It is a fully 3-D capable machine, although it is currently used on a boom.

|

|
Figure 8
To generate robot controllers, we investigate hierarchical expansions of the principled gait models to more detailed and complex representations of legged systems. In this area, we combine a refined understanding of legged system dynamics with control techniques such as quadratic regulation and virtual model control to identify controllers for legged robot platforms that inherit the robust locomotion performance of the underlying gait models. Figure 8a shows an example in which a dynamics model of the ATRIAS robot uses the selfstability control of the spring-mass model to run across rough terrain without sensing it. Figure 8b shows our current work on implementing the control on the robot.
More details about this research can be found in
- A Wu, H Geyer. Highly robust running of articulated bipeds in unobserved terrain. IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, pp. 2558 - 2565, 2014. [PDF]
- W Martin, A Wu, H Geyer. Robust Spring Mass Model Running for a Physical Bipedal Robot. IEEE International Conference on Robotics and Automation, Seattle, WA, 2015. [PDF]