
|
|
Image alignment in the presence of non-rigid distortions is a challenging task. Typically, this involves estimating the parameters of a dense deformation field that warps a distorted image back to its undistorted template. Generative approaches based on local parameter optimization can get trapped within local minima. Discriminative approaches like Nearest-Neighbor can obtain the global optimum yet with a large number of training samples that grows exponentially with the desired accuracy O((1/ε)d), the Nyquist limit to characterize an arbitrary function of dimension d. In this work, we develop Data-driven Descent (DDD) that breaks this sample limit in the case of image deformation. Specifically, it is guaranteed to converge to global optimum with significantly fewer number (O(Cdlog 1/&epsilon)) of training samples, establishing new Nyquist limit for image deformation. We analyze the behavior of our algorithm extensively using synthetic data and demonstrate successful results on experiments with complex deformations due to water and clothing.
|
Publications
"Globally Optimal Estimation of Nonrigid Image Distortion"
Yuandong Tian and Srinivasa G. Narasimhan,
International Journal of Computer Vision (IJCV).
July, 2012.
[PDF]
"A Globally Optimal Data-Driven Approach for Image Distortion
Estimation"
Yuandong Tian and Srinivasa G. Narasimhan,
Proc. of Computer Vision and Pattern Recognition (CVPR),
June, 2010.
[PDF]
"Theoretical Bounds in Distortion Estimation Algorithm."
Yuandong Tian and Srinivasa G. Narasimhan,
Technical Report CMU RI,
March, 2010.
[PDF]
|
Code and Data
Tiny fonts
Small fonts
Middle fonts
Code for the three datasets above.(Note: The code is used for local deformation only. Global deformation has to be eliminated (e.g. by tracking keypoints) before our approach can be applied.)
Densely Labeled Landmarks (first 30 frames in Middle fonts). (Video)
|
Oral Presentation and Poster
Oral Presentation [PDF, Online Video]
Poster [PDF]
|
Illustration
|
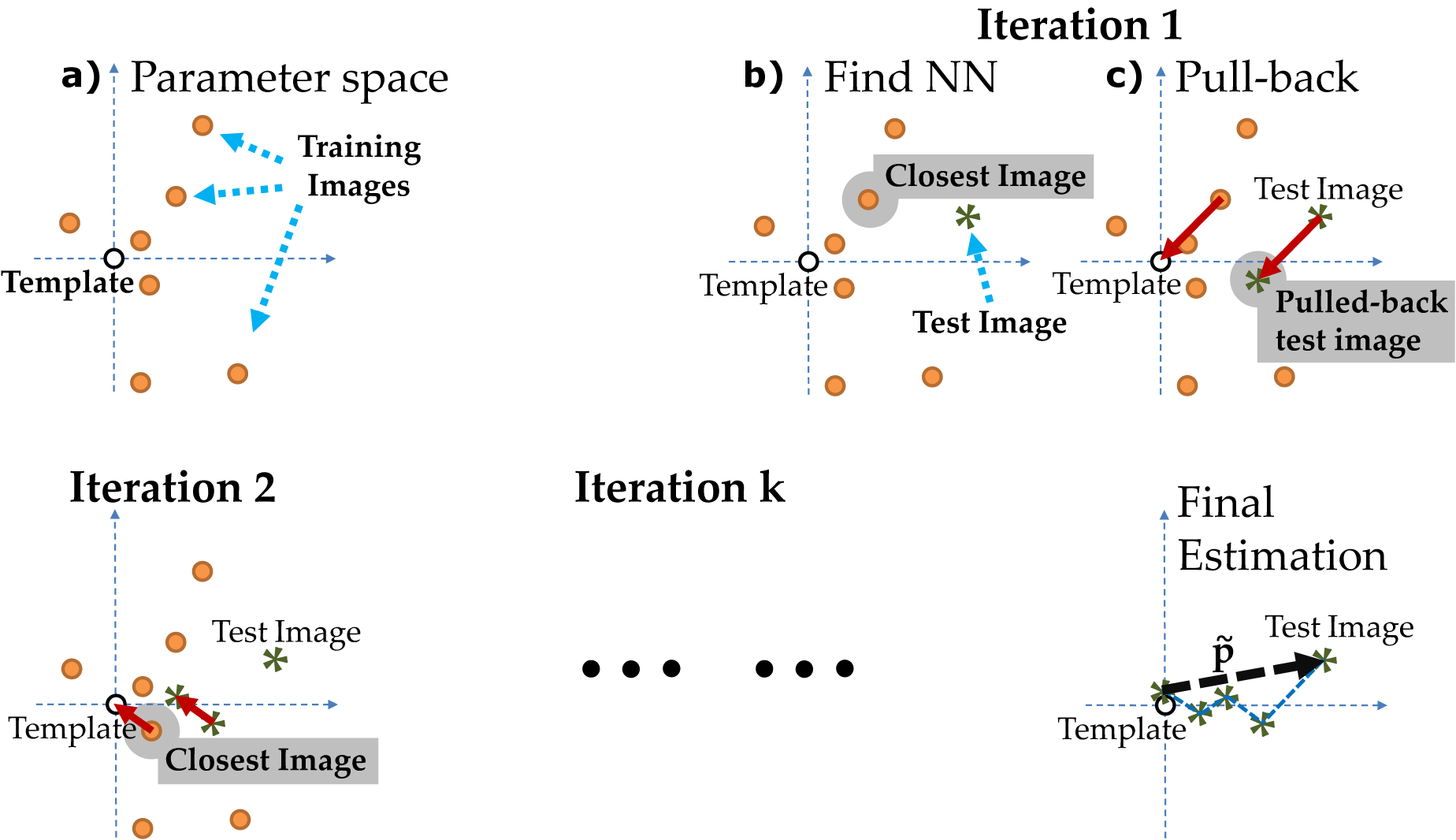
Algorithm for distortion estimation:
(a) The template (origin) T and distorted training images I with known parameters {Itr} with known parameters {ptr} are shown in the parameter space. (b) Given a distorted test image, its nearest training image (Itr, ptr) is found. (c) The test image is "pulled-back" using ptr to yield a new test image, which is closer to the template than the original one. (d) Step (b) and (c) are iterated, taking the test image closer and closer to the template. (e) The final estimate is the summation of estimations in each iteration.
|
|
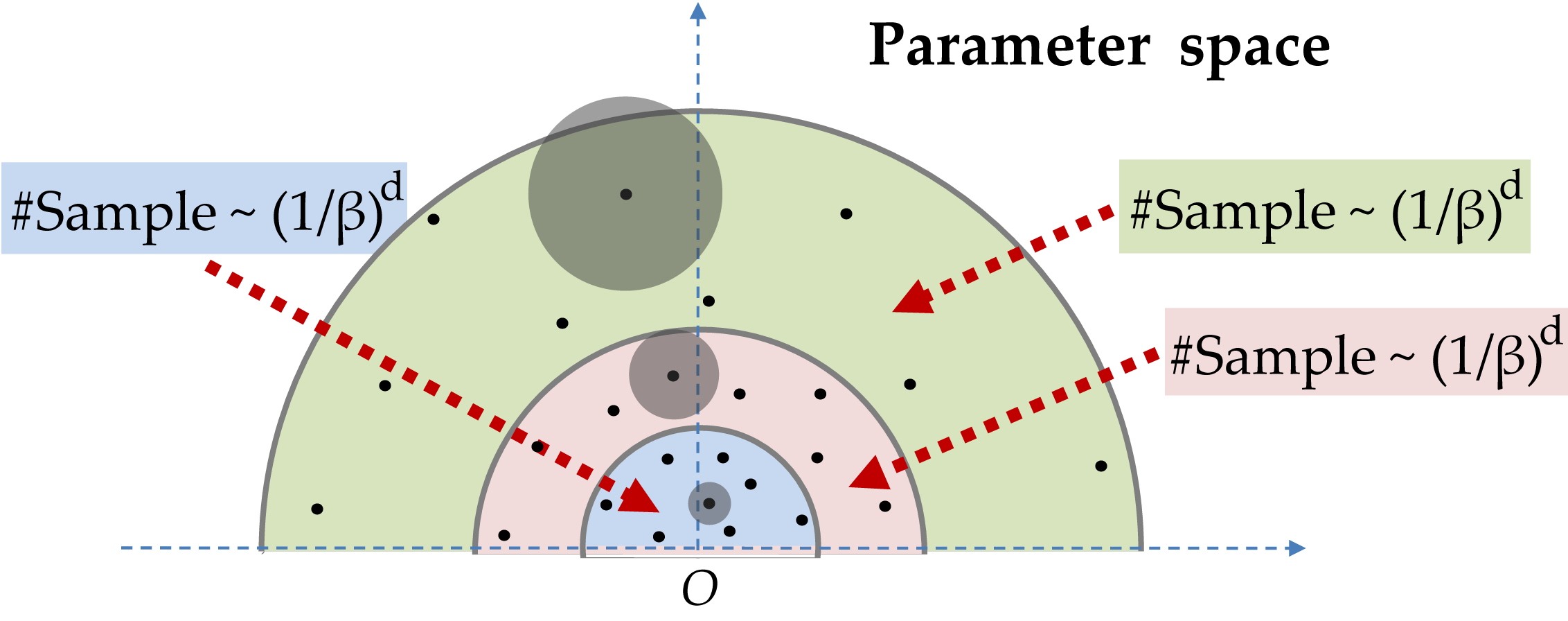
The sample distribution:
The number of samples needed to fill a give sphere ||p|| ≤ r is independent of r since the allowed prediction uncertainty (shown in gray solid circle) is proportional to r. As a result, only a small neighborhood of the origin requires dense sampling. This is the key to break the curse of dimensionality.
|
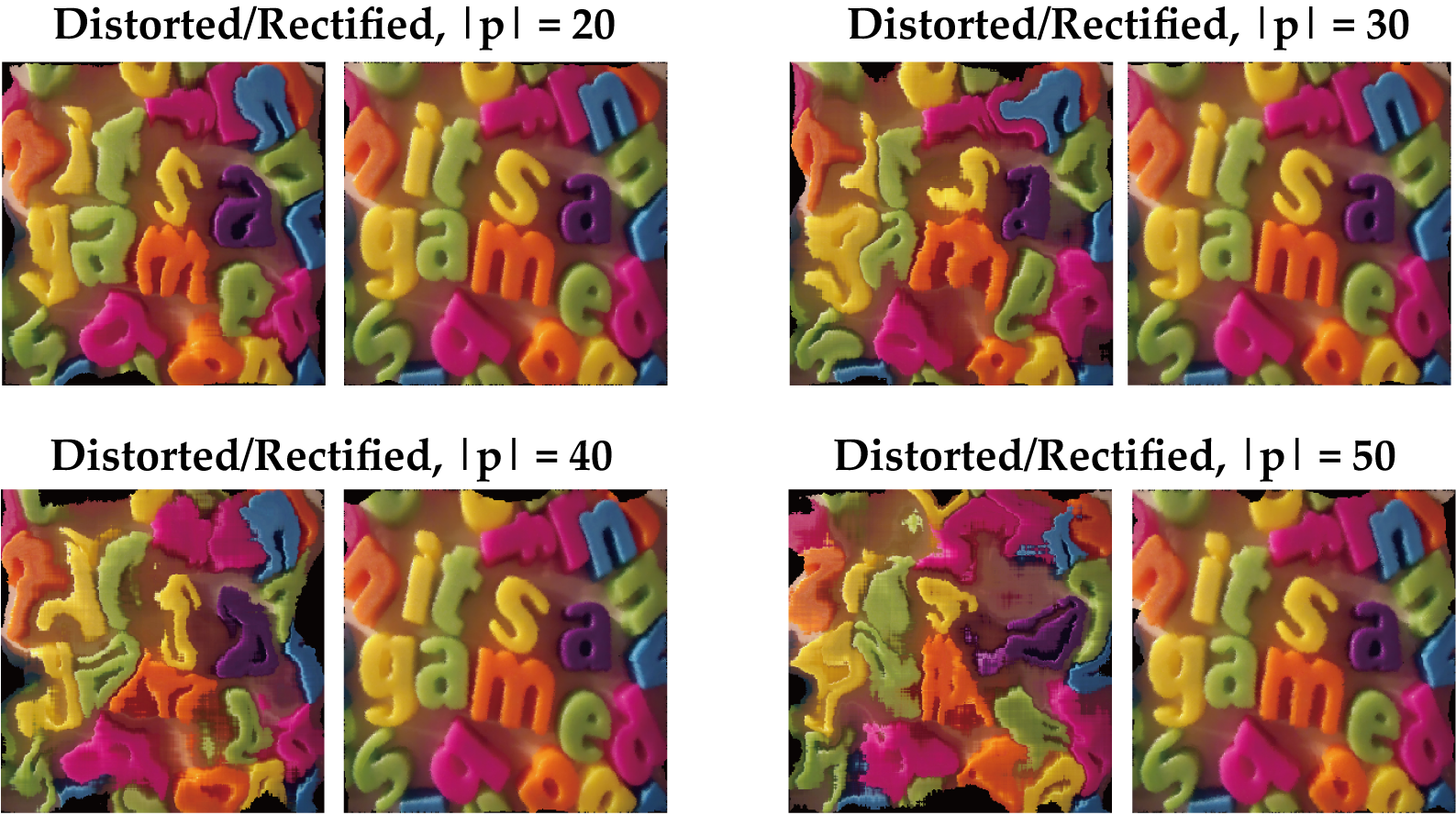
|
Sample images distorted to various degrees and the recovered rectified images:
We generated distorted images using 20 dimensional warping and rectify them using the algorithm. The algorithm did a excellent job under different degree of distortions. It rectifies the image almost perfectly.
|

|
The effects of different factors on the performance of the algorithm (synthetic data):
(a) Average convergence behavior computed over all test images. (b) The higher the number of training images, the better the performance. Note our performance is much better than nearest neighbor given the same number of samples. (c) Estimation is more accurate if the training samples are more concentrated near the origin (template). (d) Performance drops when the test image is significantly more distorted than all the training images (The black dotted line shows the average magnitude of distortions in the training images). (e) Using K-nearest neighbor with weighted voting lessens the training samples further.
|

|
Deal with local minima:
Successful convergence of our algorithm for affine transformed image, given there are at least one training sample reaching that area. In contrast, linear methods (like Lucas-Kanade) get stuck in local minima, as shown in the top-right corner.
|
|
Results

|
Text Rectification:
Rectification of water distortion on text images of different font sizes. Our approach outperforms HOG feature matching, b-spline nonrigid registration and yields slightly better results with water tracking. However, water tracking relies on the entire video frames, while our method only needs two images.
|

|
Texture Rectification:
Rectification of water distortion on 3 different colored texture images. Our method yields the best rectification.
Note the even rows show the details of the rectified images.
|
|
Videos
(Video Result Playlist)
| Original Video |
Rectified Video |
Deformation Field (dX & dY) |
Tracking |
Surface Reconstruction |
 |
 |

 |
 |
 |
 |
 |

 |
 |
 |
 |
 |

 |
 |
 |
 |
 |

 |
 |
 |
 |
 |

 |
 |
 |
 |

 |
 |
The global deformation was estimated separately using manually picked trackers. |
 |
 |

 |
 |
The global deformation was estimated separately using manually picked trackers. |
 |
 |

 |

| The global deformation was estimated separately using manually picked trackers. |
Note only the water deformations have surface reconstructions but not the cloth. For the case of cloth deformation (in particular, the last three rows), first KLT trackers are applied to obtain a rough estimation of the global deformation. Then good trackers are manually tracked to remove global deformation of the sequence. The proposed method is then applied to the rectified sequences that has no global deformation.
The second cloth (scarf) dataset comes from "Non-Rigid Structure from Locally-Rigid Motion", Jonathan Taylor, Allan D. Jepson and Kiriakos N. Kutulakos, CVPR 2010.
|
|