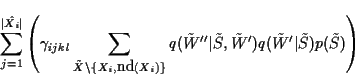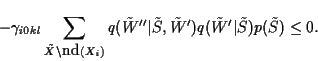

Next: Acknowledgements
Up: PROOFS
Previous: RELEVANT LEMMAS
THEOREM 2
First note that the linear fractional program in the statement of the theorem
is identical to the following program:
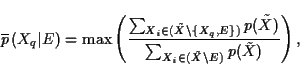 |
(7) |
subject to constraints
(5),
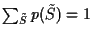 and
and
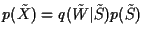 ,
where
,
where
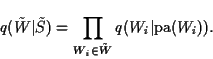 |
(8) |
Note that
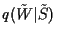 is the unique joint
distribution for
is the unique joint
distribution for 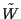 given
given 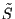 .
Uniqueness is guaranteed
by the fact that the variables in
.
Uniqueness is guaranteed
by the fact that the variables in 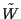 form a Bayesian network:
(1) irrelevance is equal to independence in standard Bayesian networks;
(2) Lemma 2
guarantees that all irrelevance conditions are valid when restricted to
the network of
form a Bayesian network:
(1) irrelevance is equal to independence in standard Bayesian networks;
(2) Lemma 2
guarantees that all irrelevance conditions are valid when restricted to
the network of 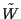 ;
(3) independence of a variable from its nondescendants given
its parents characterizes a unique Bayesian network [22].
;
(3) independence of a variable from its nondescendants given
its parents characterizes a unique Bayesian network [22].
The strategy of the proof is to demonstrate that the linear program
expressed by (7)
subject to constraints
(5),
(8) and
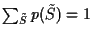 ,
is identical to program
(3) subject to
,
is identical to program
(3) subject to
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) and the unitary constraint.
and the unitary constraint.
Start from program (3).
Uniqueness of
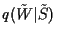 leads to constraints:
leads to constraints:
which are equivalent to the constraints summarized by
Expression (8).
Use this equality in Expressions
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) and the unitary constraint. Expression
and the unitary constraint. Expression
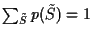 is
immediately obtained from the unitary constraint.
For constraints
is
immediately obtained from the unitary constraint.
For constraints
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) ,
divide
,
divide 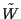 in two sets of variables;
in two sets of variables;
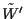 contains variables in
contains variables in 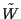 that are
nondescendants of Xi, and
that are
nondescendants of Xi, and
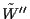 contains variables in
contains variables in 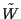 that are
descendants of Xi. Constraints
that are
descendants of Xi. Constraints
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) become:
become:
The summations involve all variables in 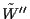 ,
so these
variables can be summed out.
Variables in
,
so these
variables can be summed out.
Variables in 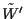 are fixed and make no reference to Xi or
any of its descendants, so they can be taken out of the summation
and cancelled. These operations reduce the inequality above to constraint
(5).
The only situation where this cancellation cannot occur is when a node
has no nondescendants; in this case, all other nodes are descendants
of the node and are summed out so the result holds.
This proves that program
(7)
subject to
(5),
(8), and
are fixed and make no reference to Xi or
any of its descendants, so they can be taken out of the summation
and cancelled. These operations reduce the inequality above to constraint
(5).
The only situation where this cancellation cannot occur is when a node
has no nondescendants; in this case, all other nodes are descendants
of the node and are summed out so the result holds.
This proves that program
(7)
subject to
(5),
(8), and
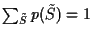 ,
is identical to program
(3) subject to
,
is identical to program
(3) subject to
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) and the unitary constraint.
and the unitary constraint.


Next: Acknowledgements
Up: PROOFS
Previous: RELEVANT LEMMAS
Fabio Gagliardi Cozman
1998-07-03
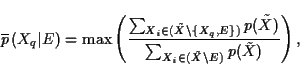
![]() is the unique joint
distribution for
is the unique joint
distribution for ![]() given
given ![]() .
Uniqueness is guaranteed
by the fact that the variables in
.
Uniqueness is guaranteed
by the fact that the variables in ![]() form a Bayesian network:
(1) irrelevance is equal to independence in standard Bayesian networks;
(2) Lemma 2
guarantees that all irrelevance conditions are valid when restricted to
the network of
form a Bayesian network:
(1) irrelevance is equal to independence in standard Bayesian networks;
(2) Lemma 2
guarantees that all irrelevance conditions are valid when restricted to
the network of ![]() ;
(3) independence of a variable from its nondescendants given
its parents characterizes a unique Bayesian network [22].
;
(3) independence of a variable from its nondescendants given
its parents characterizes a unique Bayesian network [22].
![]() ,
is identical to program
(3) subject to
,
is identical to program
(3) subject to
![]() and the unitary constraint.
and the unitary constraint.
![]() leads to constraints:
leads to constraints: