

Next: THEOREM 2
Up: PROOFS
Previous: THEOREM 1
RELEVANT LEMMAS
The following result is used in
Section 5.4:
Lemma 1
If a joint distribution satisfies constraints
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif)
,
then it satisfies
constraints
![$C_l[p(X_i\vert\mbox{pa}(X_i))]$](img63.gif)
.
To prove this result, take
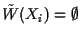 in the following lemma.
in the following lemma.
Lemma 2
Consider a joint distribution that satisfies constraints
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif)
,
and for every node
Xi,
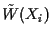
is a subset
of
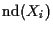
that does not overlap
with the parents of
Xi. Then the following constraints are
also satisfied:
![\begin{displaymath}
\sum_{j=1}^{\vert\hat{X_i}\vert}
\gamma_{ijkl} p(X_i = X_{ij}\vert[\mbox{pa}(X_i)]_k, \tilde{W}(X_i)) \leq
\gamma_{i0kl}.
\end{displaymath}](img66.gif) |
(6) |
Sketch of proof.
Consider an arbitrary joint distribution satisfying constraints
![$C_l[p(X_i\vert\mbox{nd}(X_i))]$](img36.gif) .
Denote the set
.
Denote the set
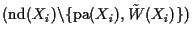 by
by
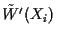 .
Obtain by marginalization the distribution of
.
Obtain by marginalization the distribution of
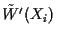 ,
,
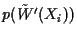 .
.
Select all constraints that are repetitions of a single original
constraint for fixed
![$[\mbox{pa}(X_i)]_k$](img70.gif) .
These constraints are all
identical, except that values of
.
These constraints are all
identical, except that values of
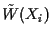 and
and
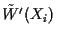 vary across constraints. Multiply every one of these constraints
by the appropriate value of
vary across constraints. Multiply every one of these constraints
by the appropriate value of
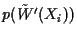 ,
and
add all constraints that refer to a particular value of
,
and
add all constraints that refer to a particular value of
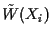 ;
constraints (6) are
then obtained after algebraic manipulations.
;
constraints (6) are
then obtained after algebraic manipulations.
Fabio Gagliardi Cozman
1998-07-03
![]() in the following lemma.
in the following lemma.
![]() .
These constraints are all
identical, except that values of
.
These constraints are all
identical, except that values of
![]() and
and
![]() vary across constraints. Multiply every one of these constraints
by the appropriate value of
vary across constraints. Multiply every one of these constraints
by the appropriate value of
![]() ,
and
add all constraints that refer to a particular value of
,
and
add all constraints that refer to a particular value of
![]() ;
constraints (6) are
then obtained after algebraic manipulations.
;
constraints (6) are
then obtained after algebraic manipulations.