IRRELEVANCE CONSTRAINTS FOR NONDESCENDANTS

Consider the constraint that, for every variable X_i, nondescendants of X_i are irrelevant to X_i given the parents of X_i. For a variable X_i, denote the nondescendants of X_i by $\mbox{nd}(X_i)$. Irrelevance constraints are satisfied by replicating the constraints $C_l[p(X_i\vert[\mbox{pa}(X_i))]_k]$ for all the values of nondescendants $\mbox{nd}(X_i)$ such that $\mbox{pa}(X_i) = [\mbox{pa}(X_i)]_k$. Denote the set of constraints obtained in this manner by $C_l[p(X_i\vert\mbox{nd}(X_i))]$. By construction, if a joint distribution satisfies constraints $C_l[p(X_i\vert\mbox{nd}(X_i))]$, then it satisfies constraints $C_l[p(X_i\vert[\mbox{pa}(X_i)]_k)]$ (Appendix A.2).

Lower bounds are calculated by forming a linear fractional program with Expression (3) subject to linear constraints $C_l[p(X_i\vert\mbox{nd}(X_i))]$ and the unitary constraint. Even though irrelevance relations introduce a large number of constraints into this program, they also introduce simplifications into the problem, as demonstrated in the remainder of this section.

Consider a Quasi-Bayesian network where a group of variables $\tilde{Z}$ is associated with credal sets. Construct the set $\tilde{S}$ containing all variables in $\tilde{Z}$ and all variables that are predecessors of variables in $\tilde{Z}$. Call $\tilde{W}$ the set of all variables that are not in $\tilde{S}$.

Theorem 2   Expression (3) can be calculated through the program:

$$\overline{p}\left( X_q\vert E \right) = \max \left( \frac{ ... ...e{S} \backslash E)} q'(\tilde{S}) p(\tilde{S}) } \right),$$ (4)

subject to $\sum_{\tilde{S}} p(\tilde{S}) = 1$ and

$$\sum_{j=1}^{\vert\hat{Z_i}\vert} \left( \gamma_{ijkl} \sum_{Z_m \in (\{\tilde{S} \} \backslash \{ Z_i,\mbox{nd}(Z_i) \})} p(\tilde{S}) \right) -$$ (5)

$$\gamma_{i0kl} \sum_{Z_m \in ( \tilde{S} \backslash \mbox{nd}(Z_i))} p(\tilde{S}) \leq$$ 0,

where the function q' is:

$$q'(\tilde{S}) = \sum_{W_i \in (\tilde{W} \backslash \{ X_q... ... \prod_{W_i \in \tilde{W}} q(W_i\vert\mbox{pa}(W_i)) \right).$$

(Proof in Appendix A.3.)

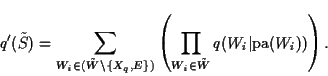
The linear fractional program in this theorem is not a problem on variables $\tilde{X}$, but a reduced maximization problem where only the values for $p(\tilde{S})$ are free to vary. A standard Bayesian network algorithm generates q' by essentially eliminating all variables in $\tilde{W}$.

The consequence of the theorem is that networks where most local credal sets are on the ``top'' of the graph can profit from irrelevance constraints. This is particularly promising in practical applications, because in general the most imprecise distributions are the priors, which are associated with nodes without parents.