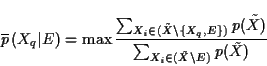LINEAR FRACTIONAL PROGRAMMING IN NATURAL EXTENSIONS

The objective here is to calculate posterior upper bounds (lower bounds are obtained by minimization):

$$\overline{p}\left( X_q\vert E \right) = \max \frac{\sum_{X_... ...{X})} {\sum_{X_i \in (\tilde{X} \backslash E)} p(\tilde{X})}$$ (3)

To guarantee that all credal sets contain valid distributions, the following unitary constraint must be added: $\sum_{\tilde{X}} p(\tilde{X}) = 1$.

The simplest natural extension is produced when no irrelevance relations are associated to a Quasi-Bayesian network [9]. In this case, the maximization in Expression (3), subject to linear constraints in Expressions (2) and the unitary constraint, is a linear fractional program. To guarantee that this linear fractional program has a solution, it is necessary to check that $\underline{p}\left( E \right)$ is non-zero; if $\underline{p}\left( E \right) = 0$, then the posterior lower envelope $\underline{p}\left( X_q\vert E \right)$ is also zero [28]. Linear fractional programs can be reduced to linear programs by a variety of methods [17,23]; consequently, Quasi-Bayesian inferences (without irrelevance relations) can be solved by linear programming techniques.