Rectification and 3D Reconstruction of Curved Document Images

Distortions in images of documents, such as the pages of books, adversely affect the performance of optical character recognition (OCR) systems. Removing such distortions requires the 3D deformation of the document that is often measured using special and precisely calibrated hardware (stereo, laser range scanning or structured light). In this paper, we introduce a new approach that automatically reconstructs the 3D shape and rectifies a deformed text document from a single image. We first estimate the 2D distortion grid in an image by exploiting the line structure and stroke statistics in text documents. This approach does not rely on more noise-sensitive operations such as image binarization and character segmentation. The regularity in the text pattern is used to constrain the 2D distortion grid to be a perspective projection of a 3D parallelogram mesh. Based on this constraint, we present a new shape-from-texture method that computes the 3D deformation up to a scale factor using SVD. Unlike previous work, this formulation imposes no restrictions on the shape (e.g., a developable surface). The estimated shape is then used to remove both geometric distortions and photometric (shading) effects in the image. We demonstrate our techniques on documents containing a variety of languages, fonts and sizes.

Publications

"Rectification and 3D Reconstruction of Curved Document Images"
Yuandong Tian and Srinivasa G. Narasimhan,
Proc. of Computer Vision and Pattern Recognition (CVPR),
June, 2011.
[PDF]

Code and Data

Download here.

Oral Presentation

Oral Presentation [PDF, Online Video]

Illustration

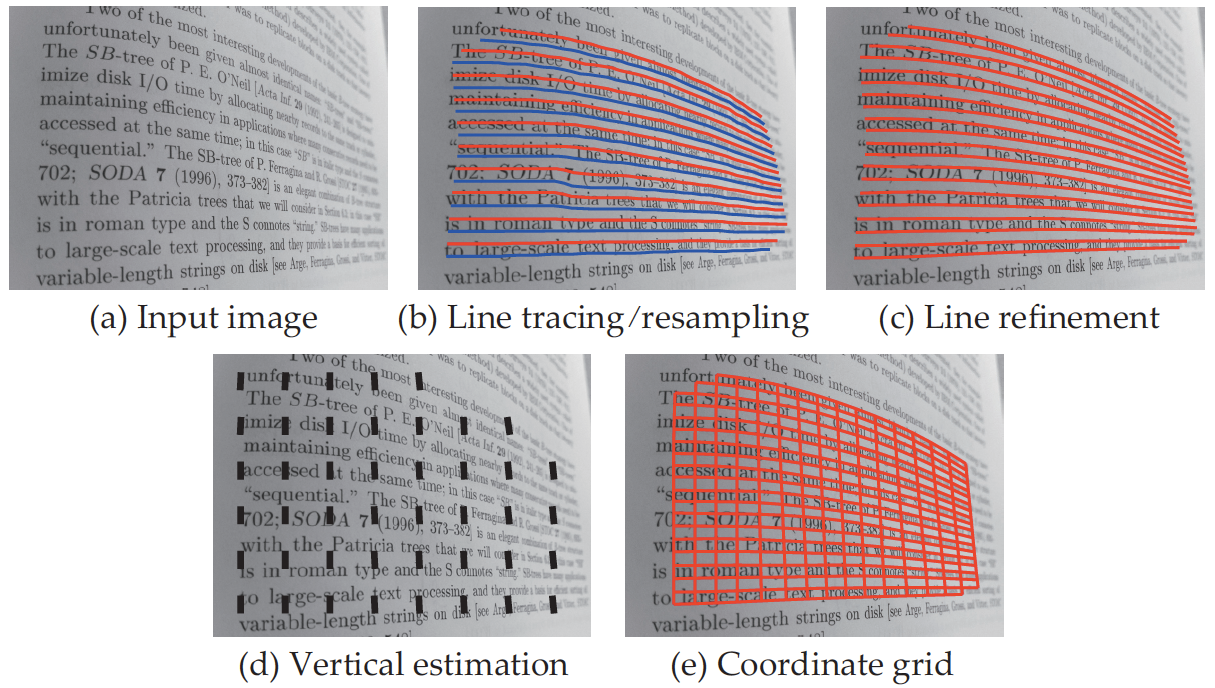
	Estimation of document image warping. (a) The original curved document image; (b) Horizontal text line tracing and resampling; (c) Text line refinement; (d) Estimation of vertical text orientation using local stroke statistics; (e) The 2D coordinate grid of the image warp obtained using horizontal tracings and text orientation. See papers for the detailed information.

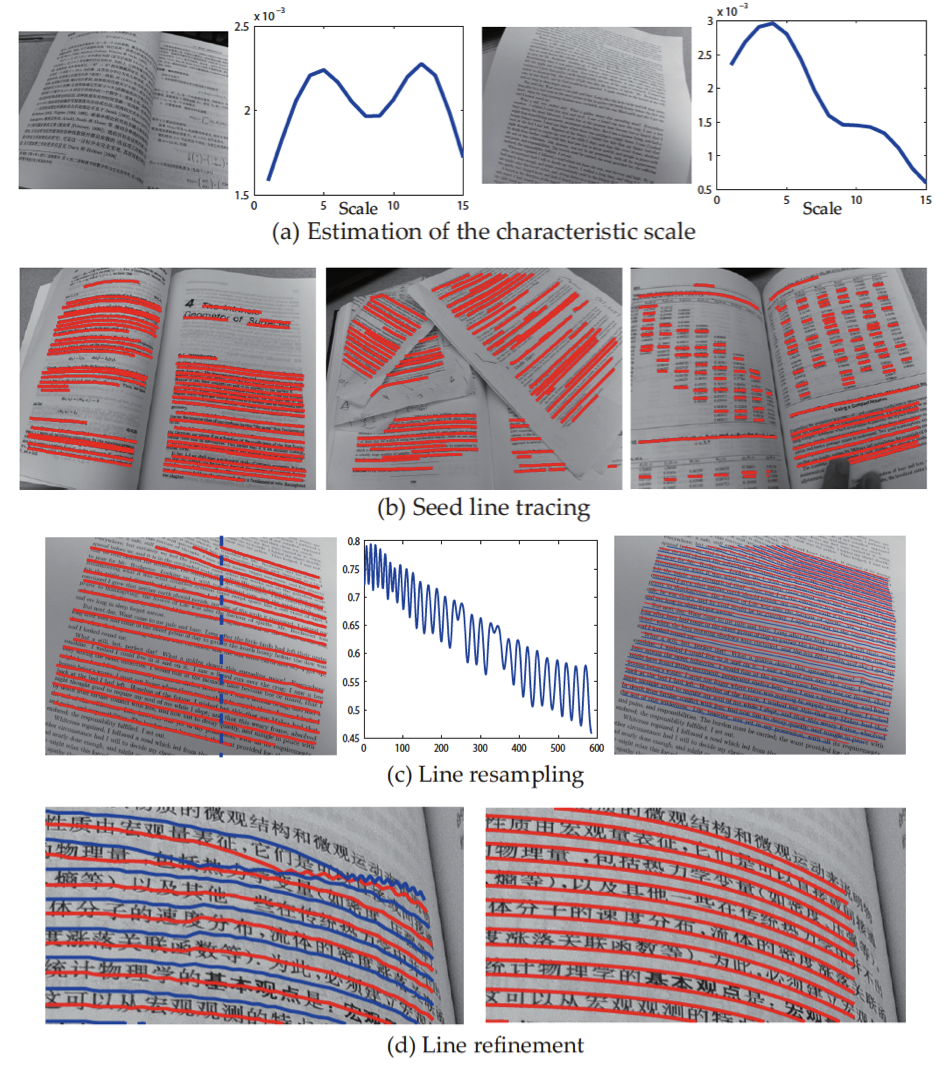
	Workflow of horizontal text line tracing. (a) The mean gradient magnitude (MGM) on each level of the image pyramid, computed by successively downsampling the document image. The first peak of MGM can be used as a characteristic scale of the text. (b) Line tracings from random starting points on document images. The tracing performs well in both text regions and white spaces. (c) Left: A set of tracings are chosen, called ``seed lines''; Middle: Mean pixel intensities computed along densely interpolated seed lines. The centers of text lines and white spaces correspond to the local extremes of the mean pixel intensities; Right: Then the top and bottom of the text lines (blue and red) are estimated, (d) and are refined by a further optimization.

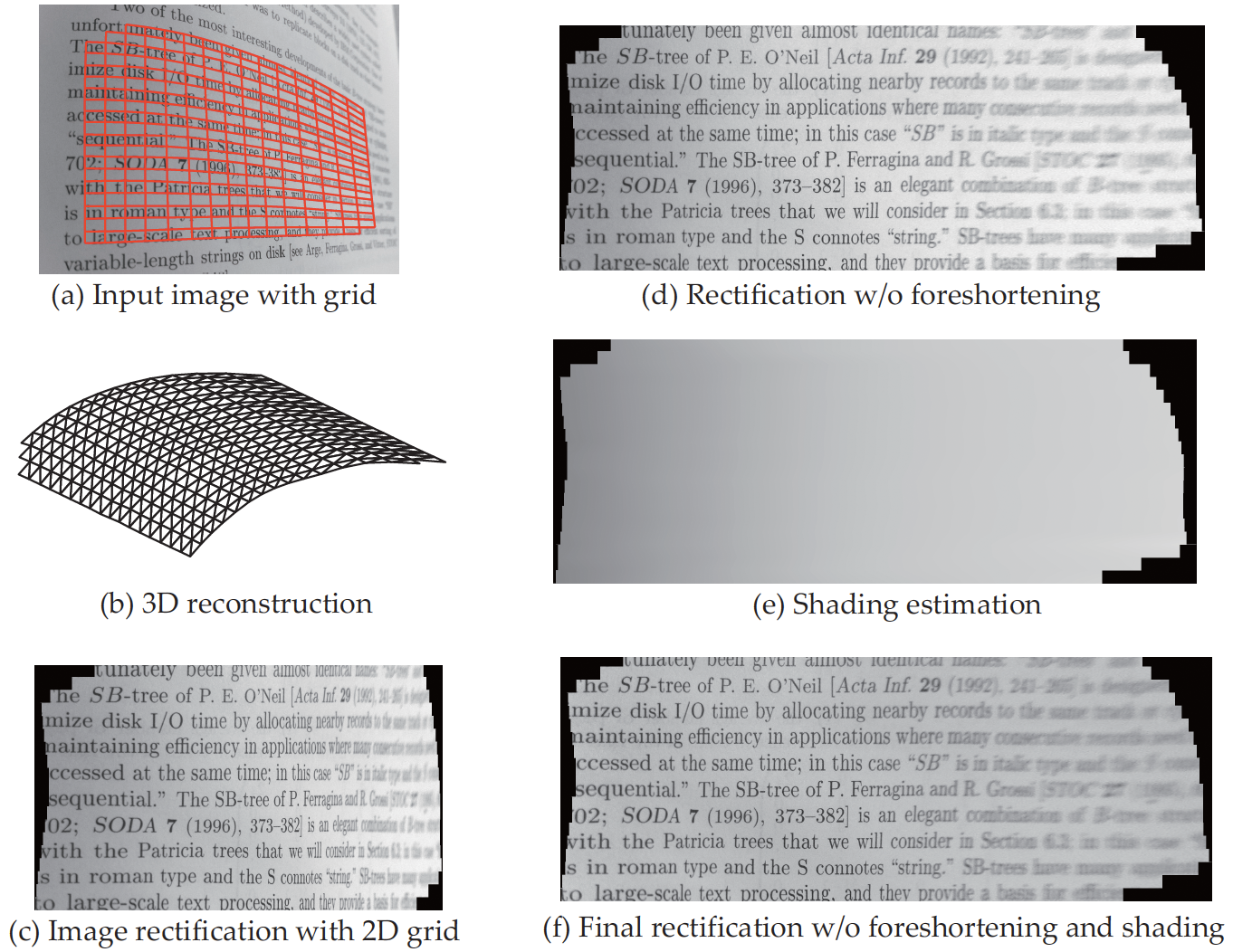
	3D reconstruction and image rectification. (a) Original image with the 2D coordinate grid; (b) 3D reconstruction from a single image; (c) Image rectification using the 2D coordinate grid. Notice the foreshortening and shading effects. Using 3D information, (d) foreshortening can be rectified. By exploiting a reflectance model (e.g. Lambertian), (e-f) shading can be estimated and normalized to yield an albedo image. See the paper for detailed information.

	3D Reconstruction from a single image (a)The basic Assumption: 4 vertices on a grid cell are situated on a parallelgram; (b)The deviation from a perfect parallelgram, measured from the 4 vertices; (c)The parametric form of each vertex, assuming perspective transform. Note Z are the depths of each vertex. (d)The objective function used to estimate the depth. It can be solved exactly using Singular Value Decomposition(SVD). See paper for more details.

Results

Rectification and 3D reconstruction from a single curved document image.

First column: Estimated 2D coordinate grid; Second column: 3D reconstruction. Third column: Rectified images. Fourth column: The insets show comparisons between rectified images (orange rectangles) and original distorted images (blue rectangles). The geometric deformations, text foreshortening and shading effects are all removed by our system. See the paper for the details.