

|
|
Conventional low frame rate cameras result in blur and/or
aliasing in images while capturing fast dynamic events. Multiple low
speed cameras have been used previously with staggered sampling to
increase the temporal resolution. However, previous approaches are
inefficient: they either use small integration time for each camera
which does not provide light benefit, or use large integration time in
a way that requires solving a big ill-posed linear system. We propose
coded sampling that address these issues: using N cameras it allows N
times temporal super-resolution while allowing N/2 times more light
compared to an equivalent high speed camera. In addition, it results in
a well-posed linear system which can be solved independently for each
frame, avoiding reconstruction artifacts and significantly reducing the
computational time and memory. Our proposed sampling uses optimal
multiplexing code considering additive Gaussian noise to achieve the
maximum possible SNR in the recovered video. We show how to implement
coded sampling on off-the-shelf machine vision cameras. We also propose
a new class of invertible codes that allow continuous blur in captured
frames, leading to an easier hardware implementation. Joint work with Amit
Agrawal, Mohit Gupta, Ashok Veeraraghavan and Srinivasa Narasimhan
|
Publication
"Optimal Coded Sampling for Temporal Super-Resolution"
Amit Agrawal, Mohit Gupta, Ashok Veeraraghavan and Srinivasa G. Narasimhan
IEEE Conference on Computer Vision and Pattern Recognition (CVPR),
June 2010.
[PDF]
|
Sampling Strategy
Suppose we have N cameras each running at frame rate f. How can we use
them to get a video with frame rate N*f? There are several sampling
schemes possible.

|
Point Sampling: Reduce the exposure time of each camera to 1/Nf
and stagger the start of integration.
Pros:
- The interleaved video automatically gives a higher frame rate
video. Blur is avoided becasue each camera captures a sharp image. N
cameras give a frame rate increase of N. No post-processing required.
Cons:
- No light benefit compared to an equivalent high speed camera
running at frame rate Nf
|
|
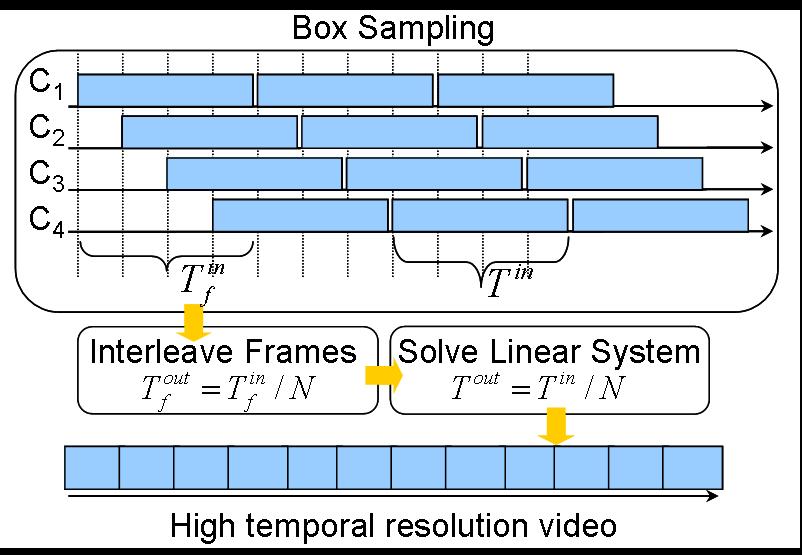
Box Sampling: Use larger exposure time for each camera (1/f) and
stagger the start of integration. The interleaved video removes
aliasing. But every frame has motion blur.
Pros:
- More light (N times) compared to an equivalent high speed camera
running at frame rate Nf
Cons:
- Box blur supppress high frequency content leading to ill-posed
system. Noise is increased in reconstruction. Requires solving a big
linear system. Dififcult to get N times increase in frame rate with N
cameras.
|

|
Coded Sampling (Ours): Use larger exposure time for each camera
(1/f), but temporally modulate every frame. Each camera has a different
code, but the code is same for all frames of a given camera.
Pros:
- Mre light (N/2 times) compared to an equivalent high speed camera
running at frame rate Nf.
- Easy to get N times increase in frame rate with N cameras.
- Codes can be chosen to get the maximum possible SNR in reconstruction.
- Coded blur leads to well-posed system which can be solved independently
for each set of N output frames. This allows streaming reconstruction
with low computational complexity (solving only a N by N linear system).
Cons:
- N/2 times more light instead of N times more light in each camera compared
to box sampling
|
|
Results

|
Figure 1: Comparison of box sampling with coded
sampling. Four captured frames (one from each camera) are shown, both
for box sampling and coded sampling. Notice the coded blur in frames
corresponding to coded blur. The box sampling can be thought of having
a code of all ones. For coded sampling, using 4 input frames, we can
get 4 output frames by solving a 4 by 4 linear system for each pixel.
This is because coded sampling is frame independent.
Note that
reconstrcuted frames are sharp with low noise. Thus, coded sampling
allows streaming output with low computation. On the other hand, for
box sampling, one needs to solve a much bigger linear system (of
several frames). Since box sampling is ill-posed it leads to increased
noise. By using regularization, noise can be reduced, but blur is
increased in the output.
|
|
|