Concave bowl on a marble slab.
There are inter-reflections inside the concave bowl and sub-surface
scattering on the translucent marble slab.
|
Image captured with a low-frequency
projected pattern. Due to inter-reflections, scene points
that are not directly lit have a large radiance. This results
in structured light decoding errors.
|
Image captured with a high-frequency
projected pattern.
Due to sub-surface scattering on the marble slab, the high frequency
pattern is blurred. Consequently, this image are not decoded accurately.
|
|
3D Reconstruction Comparison
 |
 |
 |
|
Using conventional Gray codes results in errors due to inter-reflections.
Modulated phase shifting relies on explicitly separating the direct and the
global illumination components. Hence, it suffers from low signal to noise
ratio due to low direct component on the marble slab. Our result using an
ensemble of codes has significantly fewer errors.
|
|
Designing patterns for preventing errors due to interreflections
|
Interreflections result in errors for structured light patterns
with low spatial frequencies (see paper for details). To prevent
errors due to interreflections, structured light patterns with only
high spatial frequencies must be used. Existing patterns (phase
shifting, conventional Gray codes) have patterns with a range of
spatial frequencies. We show that by using simple logical operations,
codes with only high spatial frequencies can be constructed. Below
we show an example with a V-groove scene (see paper for details).
|
|
|
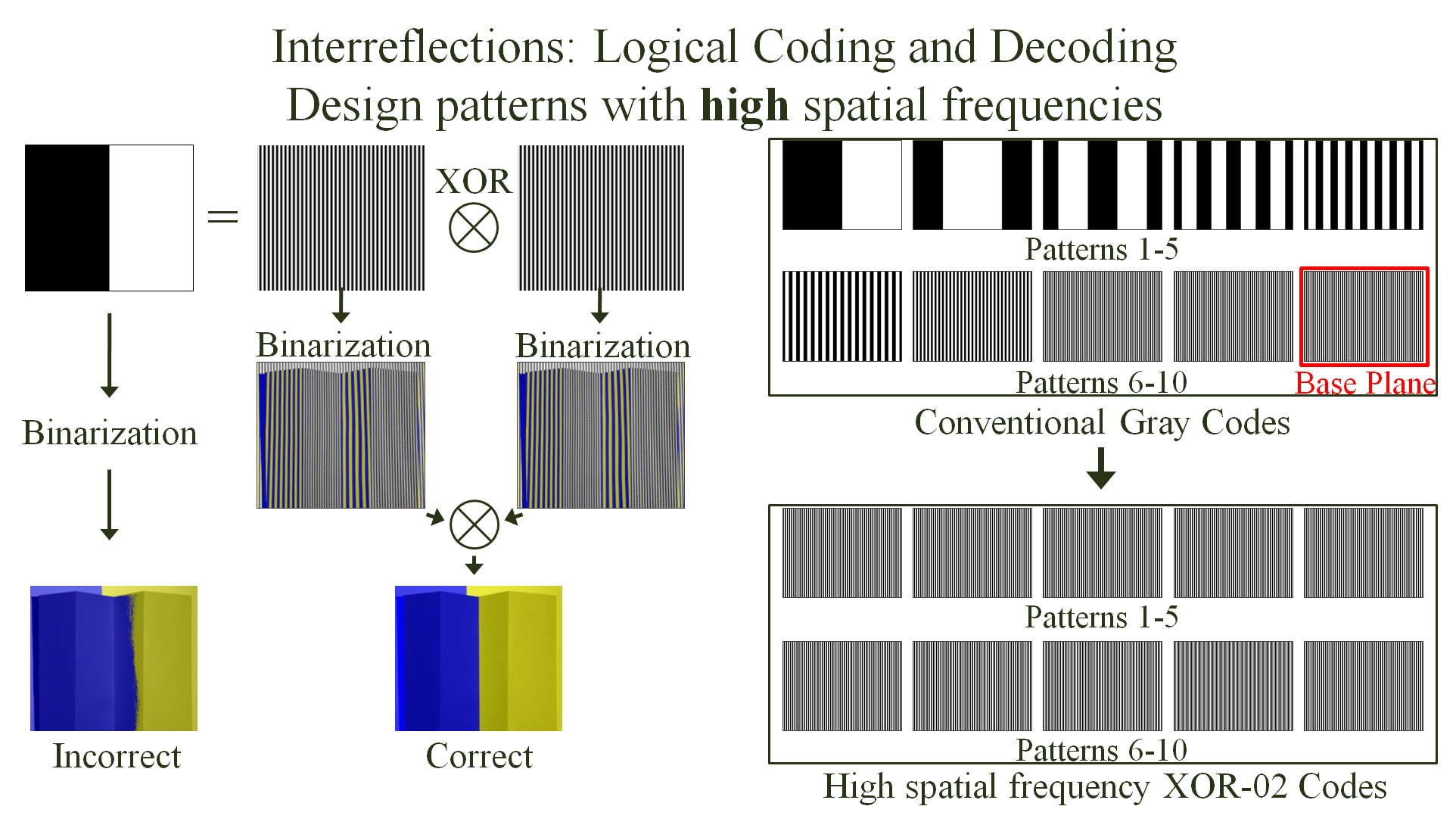
Designing patterns for sub-surface scattering and defocus
|
Local effects such as sub-surface scattering and defocus result
in blurring of incident illumination. For such effects, patterns
with low spatial frequencies must be used. We used tools from
combinatorial mathematics literature to design binary patterns
with high minimum stripe width (low spatial frequencies) as shown
below. Note the distribution of stripe widths for different codes.
|
|
|
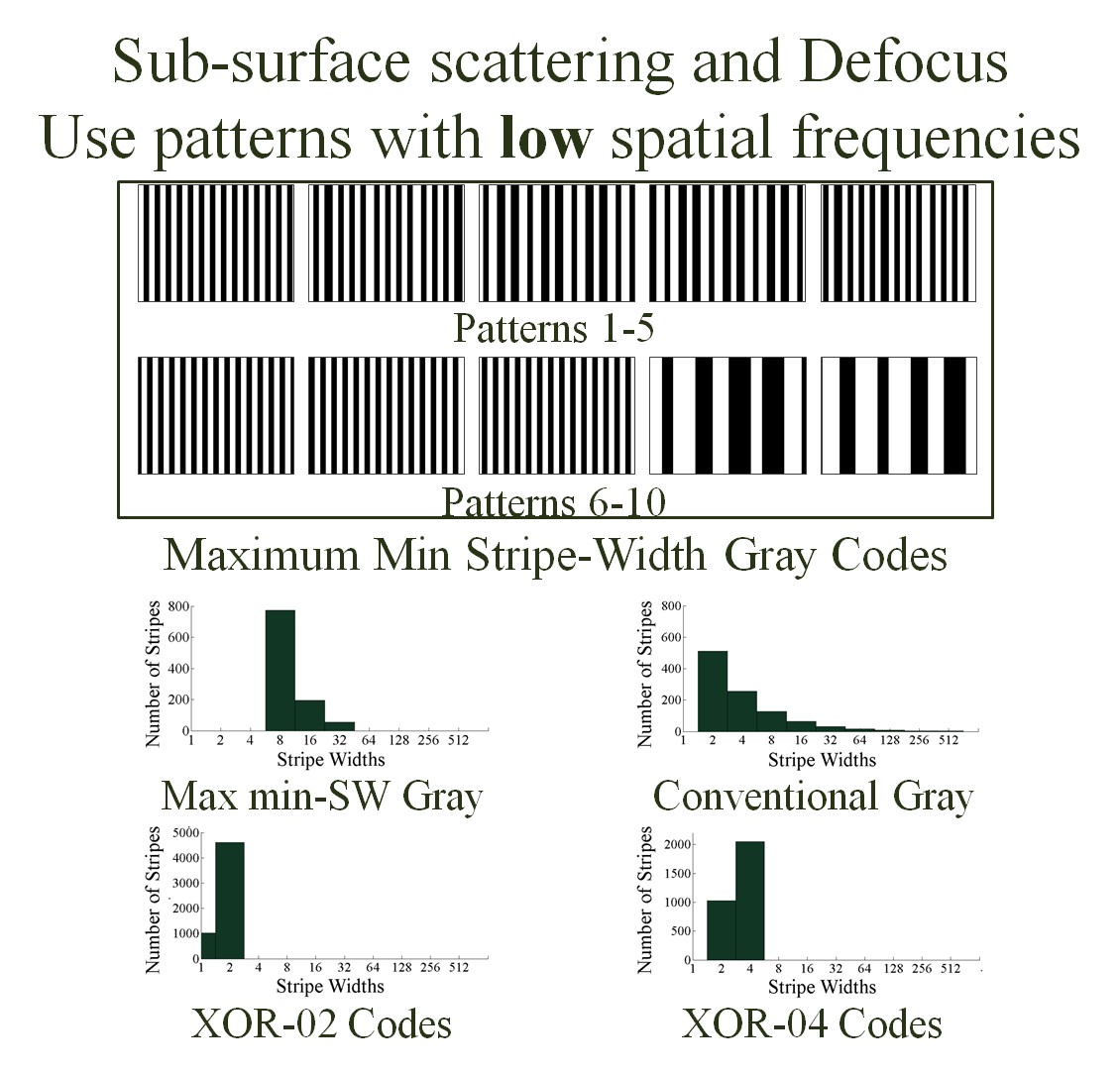
Handling scenes with multiple global illumination effects
For most scenes, we do not have a priori knowledge of the form of
global illumination effects. Moreover, many scenes can have both
interreflections (long-range) and local effects. For such scenes,
we project an ensemble of codes and perform a simple consistency check.
For example, we project four codes - two sets of logical codes
(optimized for interreflections) and two sets optimized for local effects.
For each scene point, we get four different depth values (as shown below).
The key idea is that if the codes make errors, they are random errors.
However, if any two agree, with high probability they will agree on the correct value.
|
|
|
|