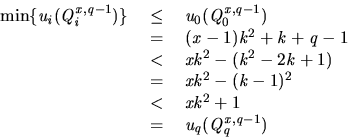Our main result on ![]() -contract paths is the following development of Theorem 3.
-contract paths is the following development of Theorem 3.
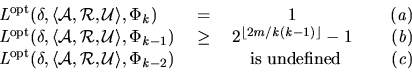
We first note that the lower bounds
(where defined) have been phrased in terms of the function ![]() as opposed to
as opposed to ![]() used in the various results on
used in the various results on ![]() -contract paths in Section 2.2. It is, of course,
the case that the bound claimed for
-contract paths in Section 2.2. It is, of course,
the case that the bound claimed for
![]() will also be a lower
bound on
will also be a lower
bound on
![]() when
when ![]() and
and ![]() holds whenever the deal
holds whenever the deal
![]() is IR. The statement of Theorem 6, however, claims rather
more than this, namely that a specific resource allocation setting
is IR. The statement of Theorem 6, however, claims rather
more than this, namely that a specific resource allocation setting
![]() can be defined for each
can be defined for each ![]() and each
and each ![]() , together
with an IR deal
, together
with an IR deal
![]() in such a way that:
in such a way that:
![]() can be achieved by a single
can be achieved by a single
![]() -contract and cannot be realised by an IR
-contract and cannot be realised by an IR ![]() -contract path. Recalling that
-contract path. Recalling that
![]() is a partial function, the latter property is equivalent to the
claim made in part (c) for the
deal
is a partial function, the latter property is equivalent to the
claim made in part (c) for the
deal
![]() of the theorem statement.
Furthermore, this same deal although achievable by an IR
of the theorem statement.
Furthermore, this same deal although achievable by an IR
![]() -contract path can be so realised
only by one whose length is as given in part (b) of the theorem statement.
-contract path can be so realised
only by one whose length is as given in part (b) of the theorem statement.
Regarding the proof itself, there are a number of notational complexities which we have
attempted to ameliorate by making some simplifying assumptions concerning the
relationship between ![]() - the size of the resource set
- the size of the resource set ![]() - and
- and ![]() - the number of agents
which are needed to realise
- the number of agents
which are needed to realise
![]() in a single IR deal. In particular, we shall
assume that
in a single IR deal. In particular, we shall
assume that ![]() is an exact multiple of
is an exact multiple of
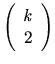 .
We observe that by employing a similar device
to that used in the proof of Theorem 4 we can
deal with cases for which
.
We observe that by employing a similar device
to that used in the proof of Theorem 4 we can
deal with cases for which ![]() does not have this property: if
does not have this property: if
![]() for integer values
for integer values ![]() and
and
![]() ,
we simply employ exactly the
same construction using
,
we simply employ exactly the
same construction using ![]() resources with the ``missing''
resources with the ``missing'' ![]() resources from
resources from
![]() being
allocated to
being
allocated to ![]() and never being reallocated within the
and never being reallocated within the ![]() -contract path. This approach accounts
for the rounding operation (
-contract path. This approach accounts
for the rounding operation (
![]() ) in the exponent term of the lower bound.
We shall also assume that the number of agents in
) in the exponent term of the lower bound.
We shall also assume that the number of agents in ![]() is exactly
is exactly ![]() .
Within the proof we use a running example for which
.
Within the proof we use a running example for which ![]() and
and ![]() to illustrate specific features.
to illustrate specific features.
We first give an outline of its structure.
Given
![]() a resource allocation setting
involving
a resource allocation setting
involving ![]() agents and
agents and ![]() resources, our aim is to define an IR
resources, our aim is to define an IR ![]() -contract path
-contract path
In order to simplify the presentation we employ a setting in
which the ![]() agents are
agents are
![]() .
Recalling that
.
Recalling that
![]() , the resource
set
, the resource
set
![]() is formed by the union of
is formed by the union of
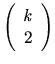 pairwise disjoint sets of size
pairwise disjoint sets of size ![]() . Given distinct
values
. Given distinct
values ![]() and
and ![]() with
with
![]() , we use
, we use
![]() to denote one of these
subsets with
to denote one of these
subsets with
![]() the
the ![]() resources
that form
resources
that form
![]() .
.
There are two main ideas underpinning the structure of each ![]() -contract in
-contract in ![]() .
.
Firstly, in the initial and subsequent allocations, the resource set
![]() is partitioned between
is partitioned between ![]() and
and ![]() and any reallocation of resources between
and any reallocation of resources between ![]() and
and ![]() that takes place within the deal
that takes place within the deal
![]() will involve only
resources in this set. Thus, for every allocation
will involve only
resources in this set. Thus, for every allocation ![]() and each pair
and each pair ![]() ,
if
,
if
![]() then
then
![]() . Furthermore,
for
. Furthermore,
for
![]() should both
should both ![]() and
and ![]() be involved, i.e.
be involved, i.e.
![]() , then this reallocation of
, then this reallocation of
![]() between
between
![]() and
and ![]() will be an
will be an ![]() -contract. That is, either exactly one element of
-contract. That is, either exactly one element of
![]() will
be moved from
will
be moved from ![]() to become a member of the allocation
to become a member of the allocation ![]() or
exactly one element of
or
exactly one element of
![]() will be moved from
will be moved from ![]() to become a member of the allocation
to become a member of the allocation ![]() .
In total, every
.
In total, every ![]() -contract
-contract ![]() in
in ![]() consists of
a simultaneous implementation of
consists of
a simultaneous implementation of
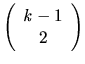
![]() -contracts: a single
-contracts: a single ![]() -contract for each of the
distinct pairs
-contract for each of the
distinct pairs ![]() of agents from the
of agents from the ![]() agents in
agents in
![]() .
.
The second key idea is to exploit one well-known property
of the ![]() -dimensional hypercube network:
for every
-dimensional hypercube network:
for every ![]() ,
,
![]() contains a
Hamiltonian cycle, i.e. a simple directed cycle formed using only the edges
of
contains a
Hamiltonian cycle, i.e. a simple directed cycle formed using only the edges
of
![]() and containing all
and containing all ![]() vertices.7
Now, suppose
vertices.7
Now, suppose
We have noted that each ![]() -contract,
-contract,
![]() that occurs in this path
that occurs in this path ![]() can be interpreted
as a set of
can be interpreted
as a set of
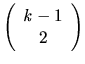 distinct
distinct ![]() -contracts. An important property
of the utility functions employed is that unless
-contracts. An important property
of the utility functions employed is that unless ![]() there will be no individually rational
there will be no individually rational
![]() -contract path that realises the deal
-contract path that realises the deal
![]() , i.e. the
, i.e. the
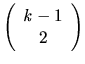
![]() -contract deals must occur simultaneously in order for the progression
from
-contract deals must occur simultaneously in order for the progression
from ![]() to
to ![]() to be IR.
Although the required deal could
be realised by a sequence of
to be IR.
Although the required deal could
be realised by a sequence of ![]() -contracts (or, more generally, any suitable
-contracts (or, more generally, any suitable ![]() -contract path),
such realisations will not describe an IR contract path.
The construction of
utility functions to guarantee such behaviour provides the principal component in showing that
the IR deal
-contract path),
such realisations will not describe an IR contract path.
The construction of
utility functions to guarantee such behaviour provides the principal component in showing that
the IR deal
![]() cannot be realised with an IR
cannot be realised with an IR ![]() -contract path: if
-contract path: if ![]() is
any allocation for which
is
any allocation for which
![]() is an
is an ![]() -contract then
-contract then
![]() is not IR.
is not IR.
We now proceed with the proof of Theorem 6.
Proof. (of Theorem 6)
Fix
![]() .
. ![]() consists of
consists of
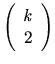 pairwise disjoint sets of
pairwise disjoint sets of ![]() resources
resources
For ![]() and
and ![]() these yield
these yield
![]() and
and


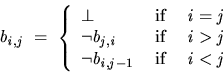

![\begin{displaymath}
B =\
\left[
{
\begin{array}{cccc}
\bot&\top&\bot&\top\\
\...
...top&\bot&\bot&\top\\
\bot&\top&\bot&\bot
\end{array}}
\right]
\end{displaymath}](img523.png)

The sequence of allocations in ![]() is built as follows.
Since
is built as follows.
Since ![]() is the immediate successor of the initial allocation
is the immediate successor of the initial allocation
![]() , it suffices to describe how
, it suffices to describe how ![]() is formed from
is formed from ![]() (when
(when ![]() ) and
) and ![]() from
from ![]() .
Let
.
Let ![]() be the allocation to be formed from
be the allocation to be formed from ![]() . The deal
. The deal
![]() will be an
will be an ![]() contract in which
contract in which
![]() . For each pair
. For each pair
![]() we have
we have
![]() in the allocation
in the allocation ![]() . In moving to
. In moving to ![]() exactly one element of
exactly one element of
![]() is reallocated between
is reallocated between
![]() and
and ![]() in such a way that in
in such a way that in ![]() ,
,
![]() , since
, since ![]() and
and ![]() are tracing complementary Hamiltonian cycles with respect to
are tracing complementary Hamiltonian cycles with respect to
![]() this ensures that
this ensures that
![]() , thereby maintaining the invariant property.
, thereby maintaining the invariant property.
Noting that for each distinct pair
![]() , we either have
, we either have
![]() allocated to
allocated to ![]() in
in ![]() or
or
![]() allocated to
allocated to ![]() in
in ![]() ,
the description just outlined indicates that the allocation
,
the description just outlined indicates that the allocation
![]() is completely specified
as follows.
is completely specified
as follows.
The cube position,, satisfies,

For each, the subset of
that is held by
in the allocation
is,

(where we recall thatThe tables below illustrates this process for our example.-bit labels in the hypercube
are identified with subsets of
.)


Now if ![]() and
and ![]() are distinct allocations generated by the process above then the
deal
are distinct allocations generated by the process above then the
deal
![]() is an
is an ![]() -contract if and only if for some
-contract if and only if for some
![]() ,
,
![]() . It follows that if
. It follows that if
![]() is an
is an ![]() -contract
for some
-contract
for some ![]() , then for some
, then for some ![]() and all
and all ![]() ,
,
![]() .
.
To determine the minimum value of ![]() with which
with which
![]() , we observe that
without loss of generality we need consider only the case
, we observe that
without loss of generality we need consider only the case ![]() , i.e. we determine the minimum number
of deals before
, i.e. we determine the minimum number
of deals before ![]() reappears. First note that in each round,
reappears. First note that in each round, ![]() , if
, if
![]() then
then
![]() , i.e. each round advances the cube position
, i.e. each round advances the cube position
![]() places:
places:
![]() and
and
![]() .
We can also observe that
.
We can also observe that
![]() for any
for any ![]() with
with ![]() , since
, since

Recalling that ![]() is the index of the
is the index of the ![]() -bit label
-bit label ![]() corresponding
to
corresponding
to
![]() in the relevant Hamiltonian cycle - i.e.
in the relevant Hamiltonian cycle - i.e.
![]() if
if
![]() ,
,
![]() if
if
![]() - we note the following properties of
the sequence of allocations defined by
- we note the following properties of
the sequence of allocations defined by ![]() that hold for each distinct
that hold for each distinct ![]() and
and ![]() .
.
The utility function ![]() is now given, for
is now given, for
![]() , by
, by

We now show that ![]() is the unique IR
is the unique IR ![]() -contract path continuation of
-contract path continuation of ![]() Suppose
Suppose
![]() is a deal that deviates from the contract
path
is a deal that deviates from the contract
path ![]() (having followed it through to the allocation
(having followed it through to the allocation ![]() ). Certainly both of the following
must hold of
). Certainly both of the following
must hold of ![]() : for each
: for each ![]() ,
,
![]() ; and there
is a
; and there
is a ![]() -tuple of pairs
-tuple of pairs
![]() with which
with which
![]() , for if either fail to be the case for some
, for if either fail to be the case for some ![]() , then
, then
![]() with the consequent effect that
with the consequent effect that ![]() and thence not IR. Now, if
and thence not IR. Now, if
![]() is the allocation that would succeed
is the allocation that would succeed ![]() in
in ![]() then
then ![]() , and
thus for at least one agent,
, and
thus for at least one agent,
![]() . It cannot be the
case that
. It cannot be the
case that
![]() corresponds to an allocation occurring strictly later
than
corresponds to an allocation occurring strictly later
than ![]() in
in ![]() since such allocations could not be realised by an
since such allocations could not be realised by an ![]() -contract.
In addition, since
-contract.
In addition, since
![]() it must be the case that
it must be the case that
![]() since exactly
since exactly ![]() cube positions in the holding of
cube positions in the holding of ![]() must change. It follows that there
are only two possibilities for
must change. It follows that there
are only two possibilities for ![]() :
: ![]() reverts to the allocation immediately
preceding
reverts to the allocation immediately
preceding ![]() or advances to the holding
or advances to the holding ![]() . It now suffices to observe
that a deal in which some agents satisfy the first of these while the remainder proceed in
accordance with the second either does not give rise to a valid allocation or cannot be realised
by an
. It now suffices to observe
that a deal in which some agents satisfy the first of these while the remainder proceed in
accordance with the second either does not give rise to a valid allocation or cannot be realised
by an ![]() -contract. On the other hand if
-contract. On the other hand if ![]() corresponds to the allocation
preceding
corresponds to the allocation
preceding ![]() then
then ![]() is not IR. We deduce, therefore, that the only IR
is not IR. We deduce, therefore, that the only IR ![]() deal
that is consistent with
deal
that is consistent with ![]() is that prescribed by
is that prescribed by ![]() .
.
This completes the analysis needed for the proof of part (b) of the theorem. It is clear that since the system
contains only ![]() agents, any deal
agents, any deal
![]() can be effected with a single
can be effected with a single ![]() -contract, thereby
establishing part (a). For part (c) - that the IR deal
-contract, thereby
establishing part (a). For part (c) - that the IR deal
![]() cannot be
realised using an individually rational
cannot be
realised using an individually rational ![]() -contract path, it suffices to observe that
since the class of IR
-contract path, it suffices to observe that
since the class of IR ![]() -contracts are a subset of the class of IR
-contracts are a subset of the class of IR ![]() -contracts, were it the
case that an IR
-contracts, were it the
case that an IR ![]() -contract path existed to implement
-contract path existed to implement
![]() , this would
imply that
, this would
imply that ![]() was not the unique IR
was not the unique IR ![]() -contract path. We have, however, proved that
-contract path. We have, however, proved that
![]() is unique, and part (c) of the theorem follows.
is unique, and part (c) of the theorem follows.![]()
We obtain a similar development of Corollary 1 in
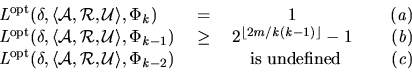
Proof. As with the proof of Corollary 1 in relation to
Theorem 3, in each case we employ the
contract path from the proof of Theorem 6, varying the definition
of
![]() in order to establish each result.
Thus let
in order to establish each result.
Thus let


In the remaining case,
![]() and
and