In principle one could attempt to construct appropriate monotone utility functions that would have the desired properties with respect to the path used in Theorem 3. It is, however, far from clear whether such a construction is possible. We do not attempt to resolve this question here. Whether an exact translation could be accomplished is, ultimately, a question of purely combinatorial interest: since our aim is to demonstrate that exponential length contract paths are needed with monotone utility functions we are not, primarily, concerned with obtaining an optimal bound.
Proof. We describe the details only for the case of ![]() being even: the result when
being even: the result when ![]() is odd is obtained
by a simple modification which we shall merely provide in outline.
is odd is obtained
by a simple modification which we shall merely provide in outline.
Let ![]() with
with ![]() . For any path
. For any path

Of course,
![]() does not describe an
does not describe an ![]() -contract path6: it is, however, not difficult to interpolate appropriate allocations,
-contract path6: it is, however, not difficult to interpolate appropriate allocations, ![]() , in
order to convert it to such a path. Consider the subsets
, in
order to convert it to such a path. Consider the subsets ![]() (with
(with ![]() ) defined
as follows:
) defined
as follows:
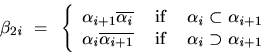
The choice for ![]() is relatively simple. Given
is relatively simple. Given
![]() ,
,

The construction for ![]() is rather more complicated. Its main idea is to make use of the fact
that the size of each set
is rather more complicated. Its main idea is to make use of the fact
that the size of each set ![]() occurring in
occurring in ![]() is very tightly
constrained:
is very tightly
constrained: ![]() is either
is either ![]() or
or ![]() according to whether
according to whether ![]() is odd or even.
We first demonstrate that
each set of size
is odd or even.
We first demonstrate that
each set of size ![]() can have at most two strict subsets (of size
can have at most two strict subsets (of size ![]() ) occurring within
) occurring within ![]() :
thus, every
:
thus, every ![]() of size
of size ![]() has exactly
has exactly ![]() or
or ![]() or
or ![]() subsets of size
subsets of size ![]() on
on ![]() .
To see this suppose the contrary.
Let
.
To see this suppose the contrary.
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() be such that
be such that ![]() with
with
We now define ![]() as
as

To show that
![]() is IR we need to demonstrate
is IR we need to demonstrate

To see that this path is the unique IR ![]() -contract path implementing
-contract path implementing
![]() ,
consider any position
,
consider any position
![]() and allocation
and allocation ![]() other than
other than
![]() or
or ![]() . It may be assumed that the deal
. It may be assumed that the deal
![]() is an
is an ![]() -contract.
If
-contract.
If ![]() then
then
![]() and
and ![]() . Hence
. Hence
![]() . In the former
case,
. In the former
case, ![]() and
and ![]() from which
from which
![]() and thus
and thus
![]() is
not IR. In the latter case
is
not IR. In the latter case ![]() since
since ![]() is a
is a ![]() from
from ![]() and
and ![]() giving
giving
![]() . Again
. Again
![]() fails to be IR since
fails to be IR since
![]() fails to give any increase in the value of
fails to give any increase in the value of ![]() . We are left with the case
. We are left with the case
![]() so that
so that
![]() and
and ![]() . Since
. Since
![]() is
assumed to be an
is
assumed to be an ![]() -contract this gives
-contract this gives
![]() . For the first possibility
. For the first possibility
![]() could not be a set on
could not be a set on ![]() :
: ![]() and
and ![]() are both subsets
of
are both subsets
of ![]() and there can be at most two such subsets occurring on
and there can be at most two such subsets occurring on ![]() . It follows,
therefore, that
. It follows,
therefore, that ![]() giving
giving
![]() so that
so that
![]() is not IR.
In the second possibility,
is not IR.
In the second possibility, ![]() but
but ![]() as
as ![]() so
the deal would result in an overall loss.
We deduce that for each
so
the deal would result in an overall loss.
We deduce that for each ![]() the only IR
the only IR ![]() -contract consistent with it is the
deal
-contract consistent with it is the
deal
![]() .
.
The final stage is to prove that the utility function ![]() is indeed a monotone
function. Suppose
is indeed a monotone
function. Suppose ![]() and
and ![]() are subsets of
are subsets of
![]() with
with ![]() . We need to show
that
. We need to show
that
![]() . We may assume that
. We may assume that ![]() , that
, that ![]() occurs as some
set within
occurs as some
set within ![]() , and that
, and that ![]() . If
. If ![]() or
or ![]() but does not occur on
but does not occur on ![]() we
have
we
have ![]() and the required inequality holds; if
and the required inequality holds; if ![]() then in order for
then in order for
![]() to be possible we would need
to be possible we would need ![]() , which would give
, which would give
![]() and this is the maximum value that any subset is assigned by
and this is the maximum value that any subset is assigned by ![]() . We are left with
only
. We are left with
only ![]() ,
, ![]() and
and ![]() on
on ![]() to consider.
It has already been shown that there are at most two subsets of
to consider.
It has already been shown that there are at most two subsets of ![]() that can occur on
that can occur on ![]() .
Consider the different possibilities:
.
Consider the different possibilities:
We conclude by observing that a similar construction can be used if ![]() is odd: use the path
is odd: use the path
![]() described above but modifying it so that one resource (
described above but modifying it so that one resource (![]() ) is always
held by
) is always
held by ![]() . Only minor modifications to the utility function definitions are needed.
. Only minor modifications to the utility function definitions are needed.![]()


Following the construction presented in Theorem 4, gives the following
utility function definitions with
![]() .
.



Proof. We again illustrate the constructions only for the case of ![]() being even, noting the
modification to deal with odd values of
being even, noting the
modification to deal with odd values of ![]() outlined at the end of the proof of Theorem 4.
The path
outlined at the end of the proof of Theorem 4.
The path ![]() is used for both cases.
is used for both cases.
For (a), we require
![]() to be defined as monotone functions with which
to be defined as monotone functions with which
![]() will be the unique cooperatively rational
will be the unique cooperatively rational ![]() -contract path to realise the cooperatively rational deal
-contract path to realise the cooperatively rational deal
![]() where
where
![]() . In this
case we set
. In this
case we set
![]() to be,
to be,
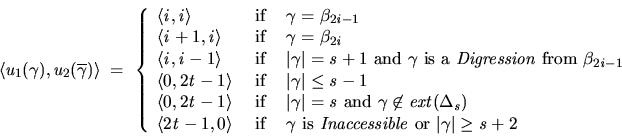
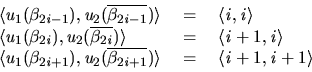
It remains only to show that these choices for
![]() define monotone utility functions.
define monotone utility functions.
Consider ![]() and
suppose
and
suppose ![]() and
and ![]() are subsets of
are subsets of
![]() with
with ![]() . If
. If ![]() , or
, or ![]() does not occur on
does not occur on ![]() then
then ![]() . If
. If ![]() or is
or is ![]() then
then ![]() which is the maximum value attainable by
which is the maximum value attainable by ![]() .
So we may assume that
.
So we may assume that ![]() , occurs on
, occurs on ![]() , i.e.
, i.e.
![]() for some
for some ![]() , and that
, and that ![]() and is either a
and is either a ![]() set or a
set or a ![]() .
From the definition of
.
From the definition of ![]() ,
, ![]() : if
: if
![]() then
then
![]() ;
if
;
if ![]() is a
is a ![]() from
from ![]() then
then
![]() .
We deduce that if
.
We deduce that if ![]() then
then
![]() , i.e.
the utility function is monotone.
, i.e.
the utility function is monotone.
Now consider ![]() with
with ![]() and
and ![]() subsets of
subsets of
![]() having
having ![]() . If
. If ![]() or
or
![]() does not occur in
does not occur in ![]() then
then ![]() its maximal value.
If
its maximal value.
If ![]() or
or
![]() is
is ![]() then
then ![]() . Thus we may
assume that
. Thus we may
assume that
![]() giving
giving ![]() and
and ![]() ,
so that
,
so that
![]() is either a
is either a
![]() or one of the
or one of the ![]() sets
sets
![]() . If
. If
![]() is
a
is
a ![]() then
then ![]() ; if it is the
; if it is the ![]() set
set ![]() then
then
![]() ; if it
is the
; if it
is the ![]() set
set ![]() then
then
![]() . It follows that
. It follows that ![]() is monotone completing
the proof of part (a).
is monotone completing
the proof of part (a).
For (b) we use,


That the choices for
![]() describe monotone utility
functions can be shown by a similar argument to that of part (a).
describe monotone utility
functions can be shown by a similar argument to that of part (a).![]()



That we can demonstrate similar extremal behaviours for contract path length with rationality
constraints in both money-based (individual rationality) and money-free (cooperative rationality,
equitable) settings irrespective of whether monotonicity properties are assumed, has some interesting
parallels with other contexts in which monotonicity is relevant. In particular we can
observe that in common with the complexity results already noted from
dunne:2003 - deciding if an allocation is Pareto optimal, if an allocation maximises ![]() ,
or if an IR
,
or if an IR ![]() -contract path exists - requiring utility functions to be monotone does not result
in a setting which is computationally more tractable.
-contract path exists - requiring utility functions to be monotone does not result
in a setting which is computationally more tractable.