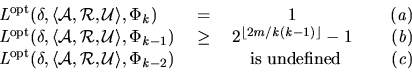Next: Related Work
Up: M(k)-contract paths
Previous: M(k)-contract paths
The device used to develop Theorem 3 to obtain the path
of Theorem 4 can be
applied to the rather more intricate construction of Theorem 6, thereby
allowing exponential lower bounds on
 to be derived.
We will merely outline the approach rather than present a detailed technical exposition.
We recall that it became relatively straightforward to define suitable monotone utility functions
once it was ensured that the subset sizes of interest - i.e. those for allocations
arising in the
to be derived.
We will merely outline the approach rather than present a detailed technical exposition.
We recall that it became relatively straightforward to define suitable monotone utility functions
once it was ensured that the subset sizes of interest - i.e. those for allocations
arising in the 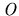 -contract path - were forced to fall into a quite restricted range. The main
difficulty that arises in applying similar methods to the path
-contract path - were forced to fall into a quite restricted range. The main
difficulty that arises in applying similar methods to the path  of Theorem 6
is the following: in the proof of Theorem 4 we consider two agents
so that converting
of Theorem 6
is the following: in the proof of Theorem 4 we consider two agents
so that converting 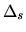 from a setting with
from a setting with  resources
in Theorem 3 to
resources
in Theorem 3 to 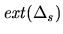 with
with  resources in Theorem 4
is achieved by combining ``complementary'' allocations, i.e.
resources in Theorem 4
is achieved by combining ``complementary'' allocations, i.e.
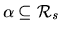 with
with
 . We can exploit
two facts, however, to develop a path
. We can exploit
two facts, however, to develop a path 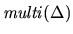 for which monotone
utility functions could be defined: the resource set
for which monotone
utility functions could be defined: the resource set
 in Theorem 6 consists of
in Theorem 6 consists of
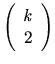 disjoint sets of size
disjoint sets of size  ; and any deal
; and any deal 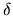 on the path
on the path  involves a reallocation
of
involves a reallocation
of
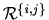 between
between  and
and 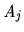 when
when
 .
Thus letting
.
Thus letting
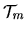 be formed by
be formed by
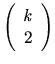 disjoint sets,
disjoint sets,
 each of size
each of size  , suppose that
, suppose that  is described
by
is described
by
with
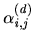 the
the  -bit label corresponding to the subset of
-bit label corresponding to the subset of 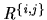 that is
held by
that is
held by  in
in 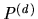 . Consider the sequence of allocations,
. Consider the sequence of allocations,
in a resource allocation setting have 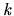 agents and
agents and  resources -
resources -
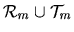 for which
for which  is characterised by
is characterised by
In this,
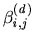 , indicates the subset of
, indicates the subset of
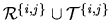 described by the
described by the  -bit label,
-bit label,
i.e.
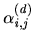 selects a subset of
selects a subset of
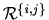 while
while
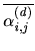 a subset of
a subset of
 .
.
It is immediate from this construction that for each allocation 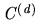 in
in 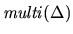 and
each
and
each  , it is always the case that
, it is always the case that
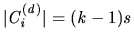 . It follows, therefore, that the
only subsets that are relevant to the definition of monotone utility functions with which
an analogous result to Theorem 6 for the path
. It follows, therefore, that the
only subsets that are relevant to the definition of monotone utility functions with which
an analogous result to Theorem 6 for the path 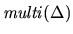 could
be derived, are those of
size
could
be derived, are those of
size  : if
: if
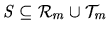 has
has 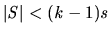 , we can fix
, we can fix
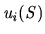 as a small enough negative value; similarly if
as a small enough negative value; similarly if 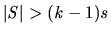 then
then 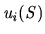 can be set to
a large enough positive
value.9
can be set to
a large enough positive
value.9
Our description in the preceding paragraphs, can be summarised in the following
result, whose proof is omitted: extending
the outline given above to a formal lower bound proof, is largely a technical exercise employing much
of the analysis already introduced, and since nothing signifcantly new is required for such
an analysis we shall not give a detailed presentation of it.
Theorem 7
Let
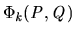
be the predicate which holds whenever

is an IR

-contract.
For all
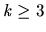
,

and
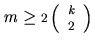
,
there is
a resource allocation setting
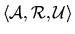
in which every

is
monotone, and an
IR deal
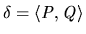
for which,



Next: Related Work
Up: M(k)-contract paths
Previous: M(k)-contract paths
Paul Dunne
2004-11-26
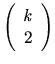 disjoint sets of size
disjoint sets of size 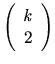 disjoint sets,
disjoint sets,
![]() in
in ![]() and
each
and
each ![]() , it is always the case that
, it is always the case that
![]() . It follows, therefore, that the
only subsets that are relevant to the definition of monotone utility functions with which
an analogous result to Theorem 6 for the path
. It follows, therefore, that the
only subsets that are relevant to the definition of monotone utility functions with which
an analogous result to Theorem 6 for the path ![]() could
be derived, are those of
size
could
be derived, are those of
size ![]() : if
: if
![]() has
has ![]() , we can fix
, we can fix
![]() as a small enough negative value; similarly if
as a small enough negative value; similarly if ![]() then
then ![]() can be set to
a large enough positive
value.9
can be set to
a large enough positive
value.9