


Next: O-contract Paths - Unrestricted
Up: Lower Bounds on Path Length
Previous: Lower Bounds on Path Length
Overview
The strategy employed in proving our results involves two parts: for a given
class of restricted contract paths we proceed as follows in obtaining
lower bounds on
 .
.
- a.
- For the contract-net graph partitioning
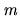 resources among
resources among 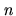 agents, construct a path,
agents, construct a path,
 realising a deal
realising a deal
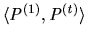 . For the
structural constraint,
. For the
structural constraint,  influencing
influencing  it is then proved that:
it is then proved that:
- a1.
- The contract path
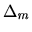 is a
is a  -path, i.e. for each
-path, i.e. for each  , the deal
, the deal
 satisfies the structural constraint
satisfies the structural constraint  .
.
- a2.
- For any pair of allocations
 and
and  occurring in
occurring in 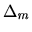 , if
, if  then the
deal
then the
deal
 is not a
is not a  -deal.
-deal.
Thus (a1) ensures that 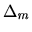 is a suitable contract path, while (a2) will guarantee that there
is exactly one allocation,
is a suitable contract path, while (a2) will guarantee that there
is exactly one allocation, 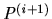 , that can be reached within
, that can be reached within 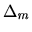 from any given
allocation
from any given
allocation  in
in 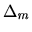 by means of a
by means of a  -deal.
-deal.
- b.
- Define utility functions
 with the following properties
with the following properties
- b1.
- The deal
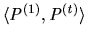 is a
is a 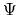 -deal.
-deal.
- b2.
- For the rationality constraint,
 influencing
influencing  , every deal
, every deal
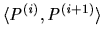 is a
is a  -deal.
-deal.
- b3.
- For every allocation
 in the contract path
in the contract path  and every allocation
and every allocation 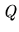 other than
other than
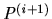 the deal
the deal
 is not a
is not a  -deal, i.e. it violates either
the stuctural constraint
-deal, i.e. it violates either
the stuctural constraint  or the rationality constraint
or the rationality constraint  .
.
Thus, (a1) and (b2) ensure that
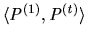 has a defined value with respect to
the function
has a defined value with respect to
the function  for the
for the 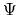 -deal
-deal
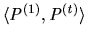 ,
i.e. a
,
i.e. a  -path realising the deal is possible. The properties
given by (a2) and (b3) indicate that (within the constructed resource allocation setting) the path
-path realising the deal is possible. The properties
given by (a2) and (b3) indicate that (within the constructed resource allocation setting) the path
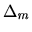 is the unique
is the unique  -path realising
-path realising
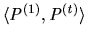 . It follows that
. It follows that
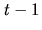 , the length of this path, gives a lower bound on the value of
, the length of this path, gives a lower bound on the value of  and hence a
lower bound on
and hence a
lower bound on
 .
.
Before continuing it will be useful to fix some notational details.
We use
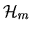 to denote the
to denote the 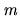 -dimensional hypercube.
Interpreted as a directed
graph,
-dimensional hypercube.
Interpreted as a directed
graph,
 has
has  vertices each of which is identified with a distinct
vertices each of which is identified with a distinct  -bit
label. Using
-bit
label. Using
 to denote an arbitrary such label,
the edges of
to denote an arbitrary such label,
the edges of
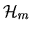 are formed by
are formed by
We identify 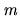 -bit labels
-bit labels
 with subsets
with subsets  of
of
 , via
, via
 if and only if
if and only if  .
Similarly, any subset
.
Similarly, any subset 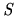 of
of  can be described by a binary word,
can be described by a binary word,  , of length
, of length 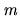 ,
i.e.
,
i.e.
 with
with  if and only if
if and only if
 . For a label
. For a label  we use
we use  to denote the number of bits with
value
to denote the number of bits with
value  , so that
, so that  is the size of the subset
is the size of the subset  . If
. If
 and
and  are
are 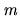 -bit labels, then
-bit labels, then  is a
is a  -bit
label, so that if
-bit
label, so that if
 and
and
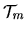 are disjoint sets, then
are disjoint sets, then  describes the union of the subset
describes the union of the subset  of
of
 with the subset
with the subset
 of
of
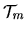 . Finally if
. Finally if
 is an
is an 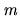 -bit
label then
-bit
label then
 denotes the label formed by changing all
denotes the label formed by changing all  values in
values in  to
to  and vice versa. In this way, if
and vice versa. In this way, if  is the subset of
is the subset of
 described
by
described
by  then
then
 describes the set
describes the set
 .
To avoid an excess of superscripts we will, where no ambiguity arises, use
.
To avoid an excess of superscripts we will, where no ambiguity arises, use  both to denote
the
both to denote
the 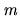 -bit label and the subset of
-bit label and the subset of
 described by it, e.g. we write
described by it, e.g. we write
 rather than
rather than
 .
.
For 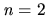 the contract-net graph induced by
the contract-net graph induced by 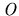 -contracts can be viewed as the
-contracts can be viewed as the 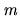 -dimensional
hypercube
-dimensional
hypercube
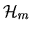 : the
: the 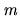 -bit label,
-bit label,  associated with a vertex of
associated with a vertex of
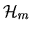 describing the allocation
describing the allocation
 to
to
 . In this way the set of IR
. In this way the set of IR
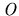 -contracts define a subgraph,
-contracts define a subgraph,
 of
of
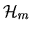 with any directed path from
with any directed path from  to
to  in
in
 corresponding to a possible IR
corresponding to a possible IR 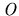 -contract path from the allocation
-contract path from the allocation
 to the allocation
to the allocation
 .
.



Next: O-contract Paths - Unrestricted
Up: Lower Bounds on Path Length
Previous: Lower Bounds on Path Length
Paul Dunne
2004-11-26
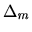 is a
is a  -path, i.e. for each
-path, i.e. for each  , the deal
, the deal
 satisfies the structural constraint
satisfies the structural constraint  .
.
 and
and  occurring in
occurring in 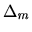 , if
, if  then the
deal
then the
deal
 is not a
is not a  -deal.
-deal.
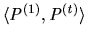 is a
is a 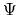 -deal.
-deal.
 influencing
influencing  , every deal
, every deal
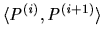 is a
is a  -deal.
-deal.
 in the contract path
in the contract path  and every allocation
and every allocation 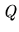 other than
other than
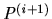 the deal
the deal
 is not a
is not a  -deal, i.e. it violates either
the stuctural constraint
-deal, i.e. it violates either
the stuctural constraint  or the rationality constraint
or the rationality constraint  .
.