Interactive theorem provers have been successfully used to formally verify safety-
critical software. However, doing so requires a significant level of resources and
expertise. A promising approach to scaling-up theorem proving and formal verification
is to augment tactic-based interactive theorem provers with machine- learning for
automation. The dominant approach in this area is to train a neural network to imitate
human experts. However, this approach is limited by the acute scarcity of
representative proofs.
An alternative approach inspired by the success of AlphaZero is to use reinforce- ment
learning instead and train an agent to interact with a theorem prover via trial and
error. Unfortunately, existing tactic-based interfaces offer unbounded action spaces
that are hardly amenable to random exploration. Such interfaces are optimized for
formalizing human insights in a concise way but often fail to define a tractable
search space for deriving those insights in the first place. Moreover, although
reinforcement learning alleviates the need for human proofs, the problem remains of
providing theorem proving tasks of suitable relevance, diversity and difficulty for
the learner.
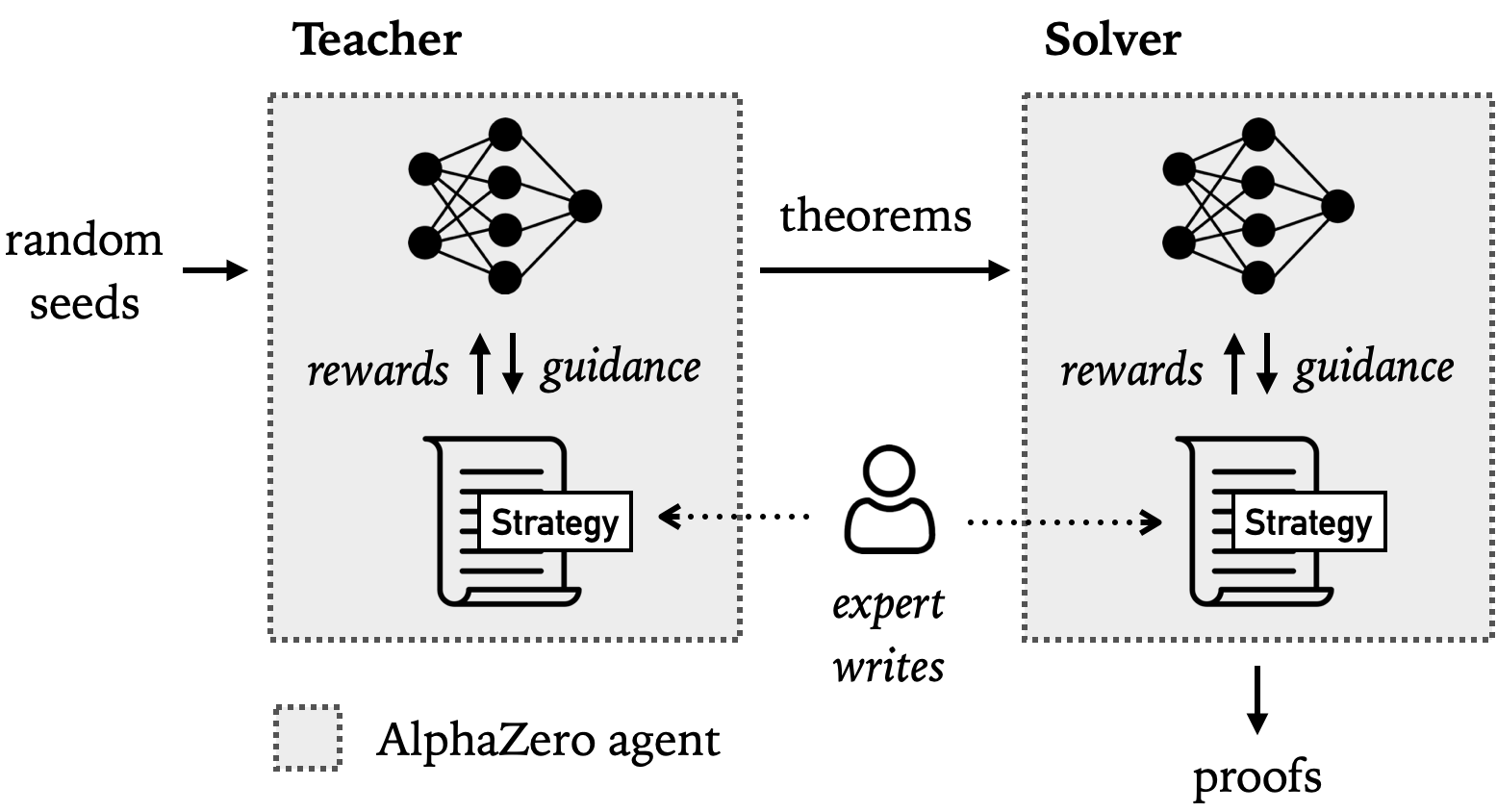
In this thesis, we propose a novel framework for theorem proving where a teacher agent
is trained to generate interesting and relevant tasks while a solver agent is co-
trained to solve them. Both agents can leverage domain-specific expert strategies in
the form of nondeterministic programs. Choice points in those programs are resolved by
neural network oracles that are trained via reinforcement learning in a
self-supervised fashion. This allows leveraging minimal amounts of domain knowledge to
tackle problems for which training data is entirely unavailable and hard to
synthesize.
This work aims to establish conceptual and engineering foundations for such a
framework. We introduce novel curriculum learning algorithms and build a new theorem
prover based on neural-guided nondeterministic programming. We introduce standard
abstractions and design principles for writing teacher and solver strategies. Finally,
we plan to evaluate our theorem prover on a collection of tasks such as loop invariant
synthesis, deductive program synthesis, arithmetic inequality proving and safe robot
planning.