Many hard control problems for real-world applications are subject to complex dynamics that are either unknown or hard to specify exactly. In addition, it is often hard for the human designer to specify what cost function should be minimized to obtain the desired behavior. For instance, think about trying to make an autonomous vehicule drive properly from a point A to a point B in a populated urban environment given input camera images. While the cost function and dynamics are hard to specify, any human driver can demonstrate the desired behavior. In these settings, it is impossible to apply traditional control/planning methods to obtain a good controller. Imitation Learning address this problem by allowing to learn a controller from demonstrations of the task by a human or expert. In this case, the objective is to obtain a controller which achieves performance as close as possible to the expert.

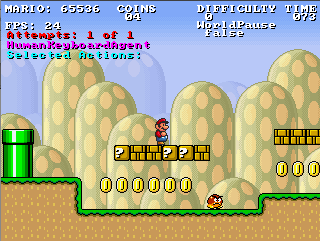
One key challenge of imitation learning is that, contrary to standard supervised learning problems, the actions outputed by the learner influences the situations it will be tested on in the future. Because of this, standard supervised learning methods can be shown to have poor performance guarantees in this setting. Hence, my research has focused on developing several new training methods that guarantees better performance on large classes of imitation learning problems that are often encountered in practice, and that are no worse than the supervised learning guarantees in the worst cases. These methods are also very efficient and can be applied on problems of similar complexity that any supervised learning method can address. So far, we have demonstrated the efficacy of these methods on two video game problems, making the computer learn how to play a 3D racing game and Mario Bros from input images and corresponding actions taken by an expert. See [AISTATS'10] and [AISTATS'11] for more details.

Many real-world applications are described by complex dynamics that are often hard to specify exactly. In such problems, autonomous controllers must trade-off between exploration, i.e. actions that allows to learn more about the sytem and improve performance in the future, and exploitation, i.e. actions that exploit current knowledge to achieve the task most efficiently.

Model-based Bayesian Reinforcement Learning provide an optimal solution to this problem given a prior specification of the initial uncertainty in the dynamics. This approach transforms the learning problem into a planning problem where the goal is to maximize expected long-term rewards under the current model uncertainty and how this uncertainty evolves in the future.

My research in this area focused on developing several extensions of Model-based Bayesian Reinforcement Learning to more complex problems, such as problems involving partial observability of the state (POMDP), continuous states, actions and observations problems (Continuous POMDP) and structured domains with several state variables (Factored MDP). For each of these extensions, I have developed efficient planning and belief monitoring algorithms which allowed to solve more complex problems than was possible with previous bayesian reinforcement learning methods. See [NIPS'07], [ICRA'08], [UAI'08] and my M.Sc. thesis for more details.

Many problems in the real-world involve the careful planning of a sequence of actions to perform in order to achieve a long-term goal or maximize some measure of performance. In many situations, uncertainty arises from various sources and must be taken into account in order to achieve the task most efficiently. For instance, the sensors and actuators of a robot are often noisy and imperfect, which yields uncertainties on the robot's current and future positions; these uncertainties must be taken into account when the robot seeks to reach a particular goal location.

The POMDP (Partially Observable Markov Decision Processes) framework allows to model such uncertainties; however, POMDPs are very difficult to solve due to their high complexity. Because most problem of interest and real world systems are modeled by huge POMDPs, it motivates the need of efficient approximate algorithms that can find near optimal solutions in a reasonable amount of time.

My research in this area focused on developing new online algorithms that can solve POMDPs efficiently during the execution of the system. Online algorithms focus on finding localy good solutions for the current situation at each decision point. This reduces greatly the set of future situations that must be considered. The particular method we developed focus computations on future events that can most improve the current solution; such as to find a solution as close as possible to the optimal as quickly as possible. See [IJCAI'07], [NIPS'07] and [JAIR'08] for more details.

Many decision problems involve several entities cooperating or competing to achieve their goal. In such problems, each entity must consider how the others will behave in order to achieve their goal most efficiently.

Under the assumption that each entity will behave such as to optimize its own payoff, game theory provide several equilibrium solutions to such problem, when every entity knows everything about the other entities. However in many situations the preferences of the other entities may be unknown and it may not be possible to observe the action and payoff of the other entities after each interaction. In such situation, the only feedback received by each entity is its own payoff, which prevents inference about the other entities payoff and behavior. In such situations, developing new learning algorithms and/or decision mecanisms that guarantee robust control in the general cases and that can achieve pareto-efficient equilibrium solutions with cooperative entities is critical.

My research in this area focused on developing a new learning algorithm that leads to pareto-efficient equilibirum when every entity behaves according to this algorithm. Other unpublished experiments have also showed that our algorithm is robust in that it tends to learn a Nash equilibrium when facing other entities that behave differently. See [CanAI'06] for more details.