



Next: Preliminaries
Up: Dimensionality reduction of Markov
Previous: Computational complexity of DR,
Contents
Moments of inter-level passage times in QBD processes
Neuts' algorithm [134,137] is an efficient algorithm that
calculates the moments of various types of passage times in very
general processes, i.e. M/G/1 type semi-Markov processes. Because of
its generality, however, the description of the algorithm in
[134,137] is sophisticated. The purpose of this section
is to make Neuts' algorithm more accessible to general readers by
re-describing his algorithm restricted to the first three
moments of inter-level passage times in QBD processes. We omit
all proofs, which are provided in detail in [134], and we
instead focus on intuition and interpretation. We include everything
needed to apply Neuts' algorithm within our solution framework, so
that general readers can apply our methodology.
Specifically, we consider a QBD process on the state space
 , which has generator matrix
, which has generator matrix 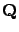 :
:
as defined in Section 3.2.
We assume that the QBD process repeats after level 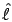 ; i.e.
; i.e.
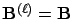 ,
,
 ,
and
,
and
 for all
for all
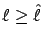 .
.
Our goal can be roughly stated as deriving the passage time required
to get from state 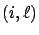 to level
to level 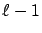 conditioned on the
particular state first reached in level
conditioned on the
particular state first reached in level 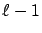 . To state our goal
more precisely, let
. To state our goal
more precisely, let
 be the event that state
be the event that state 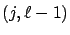 is the first state reached in level
is the first state reached in level 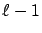 when
starting in
when
starting in 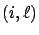 , and let
, and let
 be the time to go
from state
be the time to go
from state 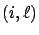 to state
to state 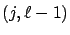 . Then, our goal is to
derive the
. Then, our goal is to
derive the
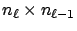 matrix,
matrix,
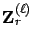 , where
, where
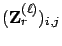 is
the
is
the  -th moment of
-th moment of
 given event
given event
 ,
for each
,
for each 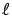 and
and 
Observe that
Hence, it suffices to derive two quantities:
The rest of this section is organized as follows. In
Section 3.7.1, we introduce some notations that we
will need along the way.
In Section 3.7.2, we derive
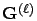 and
and
 for each
for each 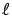 and
and 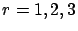 .
(Matrix
.
(Matrix
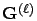 can also be obtained by the algorithm in Figure 3.12.)
In Section 3.7.3, we mention
some generalizations that Neuts' algorithm allows.
In particular, we show an extension to the passage time from level
can also be obtained by the algorithm in Figure 3.12.)
In Section 3.7.3, we mention
some generalizations that Neuts' algorithm allows.
In particular, we show an extension to the passage time from level 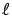 to level
to level  for
for
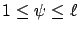 ,
which we will need in Section 3.8.
,
which we will need in Section 3.8.
Subsections




Next: Preliminaries
Up: Dimensionality reduction of Markov
Previous: Computational complexity of DR,
Contents
Takayuki Osogami
2005-07-19
![]() , which has generator matrix
, which has generator matrix ![]() :
:
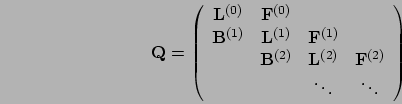
![]() to level
to level ![]() conditioned on the
particular state first reached in level
conditioned on the
particular state first reached in level ![]() . To state our goal
more precisely, let
. To state our goal
more precisely, let
![]() be the event that state
be the event that state ![]() is the first state reached in level
is the first state reached in level ![]() when
starting in
when
starting in ![]() , and let
, and let
![]() be the time to go
from state
be the time to go
from state ![]() to state
to state ![]() . Then, our goal is to
derive the
. Then, our goal is to
derive the
![]() matrix,
matrix,
![]() , where
, where
![]() is
the
is
the ![]() -th moment of
-th moment of
![]() given event
given event
![]() ,
for each
,
for each ![]() and
and ![]()
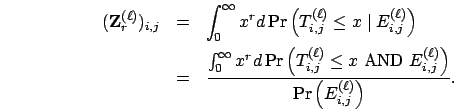
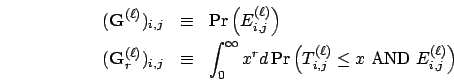
![]() and
and
![]() for each
for each ![]() and
and ![]() .
(Matrix
.
(Matrix
![]() can also be obtained by the algorithm in Figure 3.12.)
In Section 3.7.3, we mention
some generalizations that Neuts' algorithm allows.
In particular, we show an extension to the passage time from level
can also be obtained by the algorithm in Figure 3.12.)
In Section 3.7.3, we mention
some generalizations that Neuts' algorithm allows.
In particular, we show an extension to the passage time from level ![]() to level
to level ![]() for
for
![]() ,
which we will need in Section 3.8.
,
which we will need in Section 3.8.