



Next: Example
Up: Moments of inter-level passage
Previous: Moments of inter-level passage
Contents
Preliminaries
We first define the transition probability matrix,  ,
such that its
,
such that its  element,
element,
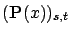 , represents the
probability that (i) the sojourn time at state
, represents the
probability that (i) the sojourn time at state 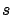 is
is  AND
(ii) the first transition out of state
AND
(ii) the first transition out of state 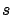 is to state
is to state  .
(Note that state
.
(Note that state 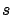 denotes a state (
denotes a state ( ), where
), where
 .
State
.
State  is defined analogously.)
By the following Lemma, which follows from the memoryless property
of the exponential distribution,
is defined analogously.)
By the following Lemma, which follows from the memoryless property
of the exponential distribution,
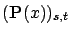 is also the product of the
probabilities of events (i) and (ii).
is also the product of the
probabilities of events (i) and (ii).
Lemma 7
Let  and
and  be independent exponential random variables.
Let
be independent exponential random variables.
Let
 . Then
. Then
Matrix  has the same structural shape as
has the same structural shape as  , although its
entries are different, and thus it can be represented in terms
of submatrices, analogous to those in
, although its
entries are different, and thus it can be represented in terms
of submatrices, analogous to those in  , indicating backward transitions,
local transitions, and forward
transitions, as follows:
, indicating backward transitions,
local transitions, and forward
transitions, as follows:
Specifically,
the  element of
element of
 is the probability that the sojourn time in state
is the probability that the sojourn time in state 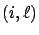 is
is  AND the first transition out of state
AND the first transition out of state 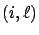 is to state
is to state 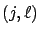 .
Likewise,
the
.
Likewise,
the  element of
element of
 (respectively,
(respectively,
 )
is the probability that the sojourn time in state
)
is the probability that the sojourn time in state 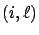 is
is  AND the first transition out of state
AND the first transition out of state 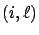 is to state
is to state  (respectively, to state
(respectively, to state 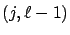 ).
).
Next, we define the  -th moment of submatrices,
-th moment of submatrices,
 ,
,
 ,
,
 , as follows:
, as follows:
for 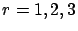 , and
, and 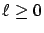 , where an integral of a matrix
, where an integral of a matrix 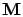 is a
matrix of the integrals of the elements in
is a
matrix of the integrals of the elements in 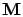 .
For the repeating part, we define
.
For the repeating part, we define
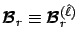 ,
,
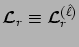 , and
, and
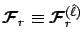 ,
omitting the superscript.
,
omitting the superscript.
We now define the limits as
 of
of
 ,
,
 , and
, and
 as follows:
as follows:
for 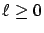 .
For the repeating part, we define
.
For the repeating part, we define
 ,
,
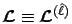 , and
, and
 ,
omitting the superscript.
,
omitting the superscript.
Subsections




Next: Example
Up: Moments of inter-level passage
Previous: Moments of inter-level passage
Contents
Takayuki Osogami
2005-07-19
![]() ,
such that its
,
such that its ![]() element,
element,
![]() , represents the
probability that (i) the sojourn time at state
, represents the
probability that (i) the sojourn time at state ![]() is
is ![]() AND
(ii) the first transition out of state
AND
(ii) the first transition out of state ![]() is to state
is to state ![]() .
(Note that state
.
(Note that state ![]() denotes a state (
denotes a state (![]() ), where
), where
![]() .
State
.
State ![]() is defined analogously.)
By the following Lemma, which follows from the memoryless property
of the exponential distribution,
is defined analogously.)
By the following Lemma, which follows from the memoryless property
of the exponential distribution,
![]() is also the product of the
probabilities of events (i) and (ii).
is also the product of the
probabilities of events (i) and (ii).

![]() -th moment of submatrices,
-th moment of submatrices,
![]() ,
,
![]() ,
,
![]() , as follows:
, as follows:
![]() of
of
![]() ,
,
![]() , and
, and
![]() as follows:
as follows: