

Next: Modifying the Sampling Distribution
Up: AIS-BN: Adaptive Importance Sampling
Previous: AIS-BN: Adaptive Importance Sampling
Basic Algorithm -- AIS-BN
Compared with importance sampling used in normal
finite-dimensional integrals, importance sampling used in Bayesian
networks has several significant advantages. First, the network
joint probability distribution
Pr( ) is decomposable
and can be factored into component parts. Second, the network has
a clear structure, which represents many conditional independence
relationships. These properties are very helpful in estimating the
optimal importance function.
) is decomposable
and can be factored into component parts. Second, the network has
a clear structure, which represents many conditional independence
relationships. These properties are very helpful in estimating the
optimal importance function.
The basic AIS-BN algorithm is presented in Figure 2.
The main differences between the AIS-BN algorithm and the basic
importance sampling algorithm in Figure 1 is that we
introduce a monotonically increasing weight function wk and two
effective heuristic initialization methods in Step 2. We also
introduce a special learning component in Step 7 to let the
updating process run more smoothly, avoiding oscillation of the
parameters. The score processing in Step 10 is
wiScore =
wk
.
Note that in this respect the algorithm in Figure 1
becomes a special case of AIS-BN when wk = 1. The reason why we
use wk is that we want to give different weights to the
sampling results obtained at different stages of the algorithm. As
each stage updates the importance function, they will all have
different distance from the optimal importance function. We
recommend that
wk 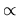 1/
1/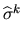 , where
, where
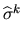 is the standard deviation estimated in
stage k using Equation 3.1 In
order to keep wk monotonically increasing, if wk is smaller
than wk - 1, we adjust its value to wk - 1. This weighting
scheme may introduce bias into the final result. Since the initial
importance sampling functions are often inefficient and introduce
big variance into the results, we also recommend that wk = 0 in
the first few stages of the algorithm. We have designed this
weighting scheme to reflect the fact that in practice estimates
with very small estimated variance are usually good estimates.
is the standard deviation estimated in
stage k using Equation 3.1 In
order to keep wk monotonically increasing, if wk is smaller
than wk - 1, we adjust its value to wk - 1. This weighting
scheme may introduce bias into the final result. Since the initial
importance sampling functions are often inefficient and introduce
big variance into the results, we also recommend that wk = 0 in
the first few stages of the algorithm. We have designed this
weighting scheme to reflect the fact that in practice estimates
with very small estimated variance are usually good estimates.


Next: Modifying the Sampling Distribution
Up: AIS-BN: Adaptive Importance Sampling
Previous: AIS-BN: Adaptive Importance Sampling
Jian Cheng
2000-10-01
![]() ) is decomposable
and can be factored into component parts. Second, the network has
a clear structure, which represents many conditional independence
relationships. These properties are very helpful in estimating the
optimal importance function.
) is decomposable
and can be factored into component parts. Second, the network has
a clear structure, which represents many conditional independence
relationships. These properties are very helpful in estimating the
optimal importance function.
 .
.