

Next: A Generic Importance Sampling
Up: Importance Sampling Algorithms for
Previous: Importance Sampling Algorithms for
Mathematical Foundations
Let
g( ) be a function of m variables
) be a function of m variables
 = (X1,..., Xm) over a domain
= (X1,..., Xm) over a domain

 Rm, such that
computing
g(
Rm, such that
computing
g( ) for any
) for any  is feasible. Consider the
problem of approximate computation of the integral
is feasible. Consider the
problem of approximate computation of the integral
Importance sampling approaches this problem by writing the
integral (1) as
where
f ( ), often referred to as the importance
function, is a probability density function over
), often referred to as the importance
function, is a probability density function over  .
f (
.
f ( ) can be used in importance sampling if there exists an
algorithm for generating samples from
f (
) can be used in importance sampling if there exists an
algorithm for generating samples from
f ( ) and if the
importance function is zero only when the original function is
zero, i.e.,
g(
) and if the
importance function is zero only when the original function is
zero, i.e.,
g( )
)
 0
0  f (
f ( )
)  0.
0.
After we have independently sampled n points 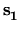 ,
, 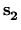 , ...,
, ..., 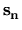 ,
,
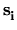
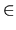
 , according to the
probability density function
f (
, according to the
probability density function
f ( ), we can estimate the
integral I by
), we can estimate the
integral I by
and estimate the variance of  by
It is straightforward to show that this estimator has the
following properties:
by
It is straightforward to show that this estimator has the
following properties:
-
E(
 ) = I
) = I
-
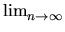
 = I
= I
-
 . (
. ( - I)
- I)  Normal(0,
Normal(0,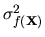 ), where
), where
-
E
 (
( )
) =
= 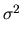 (
( ) =
) = 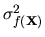 /n
/n
The variance of  is proportional to
is proportional to
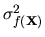 and inversely proportional to the number of samples. To
minimize the variance of
and inversely proportional to the number of samples. To
minimize the variance of  , we can either increase the
number of samples or try to decrease
, we can either increase the
number of samples or try to decrease
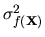 . With
respect to the latter, Rubinstein [1981] reports the
following useful theorem and corollary.
. With
respect to the latter, Rubinstein [1981] reports the
following useful theorem and corollary.
Theorem 1
The minimum of
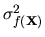
is equal to
and occurs when

is distributed according to the
following probability density function
f (
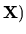
=
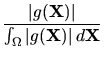
.
Corollary 1
If
g(
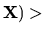
0, then the optimal probability density function
is
f (
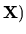
=

and
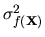
= 0.
Although in practice sampling from precisely
f ( ) = g(
) = g( )/I will occur rarely, we expect that functions that are close
enough to it can still reduce the variance effectively. Usually,
the closer the shape of the function
f (
)/I will occur rarely, we expect that functions that are close
enough to it can still reduce the variance effectively. Usually,
the closer the shape of the function
f ( ) is to the shape
of the function
g(
) is to the shape
of the function
g( ), the smaller is
), the smaller is
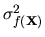 . In high-dimensional integrals, selection of the
importance function,
f (
. In high-dimensional integrals, selection of the
importance function,
f ( ), is far more critical than
increasing the number of samples, since the former can
dramatically affect
), is far more critical than
increasing the number of samples, since the former can
dramatically affect
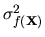 . It seems prudent to
put more energy in choosing an importance function whose shape is
as close as possible to that of
g(
. It seems prudent to
put more energy in choosing an importance function whose shape is
as close as possible to that of
g( ) than to apply the
brute force method of increasing the number of samples.
) than to apply the
brute force method of increasing the number of samples.
It is worth noting here that if
f ( ) is uniform,
importance sampling becomes a general Monte Carlo sampling.
Another noteworthy property of importance sampling that can be
derived from Equation 4 is that we should avoid
f (
) is uniform,
importance sampling becomes a general Monte Carlo sampling.
Another noteworthy property of importance sampling that can be
derived from Equation 4 is that we should avoid
f ( )
) 
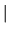 g(
g( ) - I . f (
) - I . f ( )
)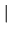 in any
part of the domain of sampling, even if
f (
in any
part of the domain of sampling, even if
f ( ) matches well
g(
) matches well
g( )/I in important regions. If
f (
)/I in important regions. If
f ( )
) 
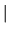 g(
g( ) - I . f (
) - I . f ( )
)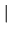 , the variance can become very
large or even infinite. We can avoid this by adjusting
f (
, the variance can become very
large or even infinite. We can avoid this by adjusting
f ( ) to be larger in unimportant regions of the domain of
) to be larger in unimportant regions of the domain of  .
.
While in this section we discussed importance sampling for
continuous variables, the results stated are valid for discrete
variables as well, in which case integration should be substituted
by summation.


Next: A Generic Importance Sampling
Up: Importance Sampling Algorithms for
Previous: Importance Sampling Algorithms for
Jian Cheng
2000-10-01
![]() ) be a function of m variables
) be a function of m variables
![]() = (X1,..., Xm) over a domain
= (X1,..., Xm) over a domain
![]()
![]() Rm, such that
computing
g(
Rm, such that
computing
g(![]() ) for any
) for any ![]() is feasible. Consider the
problem of approximate computation of the integral
is feasible. Consider the
problem of approximate computation of the integral
![]() ,
, ![]() , ...,
, ..., ![]() ,
,
![]()
![]()
![]() , according to the
probability density function
f (
, according to the
probability density function
f (![]() ), we can estimate the
integral I by
), we can estimate the
integral I by
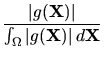 .
.
![]() ) is uniform,
importance sampling becomes a general Monte Carlo sampling.
Another noteworthy property of importance sampling that can be
derived from Equation 4 is that we should avoid
f (
) is uniform,
importance sampling becomes a general Monte Carlo sampling.
Another noteworthy property of importance sampling that can be
derived from Equation 4 is that we should avoid
f (![]() )
) ![]()
![]() g(
g(![]() ) - I . f (
) - I . f (![]() )
)![]() in any
part of the domain of sampling, even if
f (
in any
part of the domain of sampling, even if
f (![]() ) matches well
g(
) matches well
g(![]() )/I in important regions. If
f (
)/I in important regions. If
f (![]() )
) ![]()
![]() g(
g(![]() ) - I . f (
) - I . f (![]() )
)![]() , the variance can become very
large or even infinite. We can avoid this by adjusting
f (
, the variance can become very
large or even infinite. We can avoid this by adjusting
f (![]() ) to be larger in unimportant regions of the domain of
) to be larger in unimportant regions of the domain of ![]() .
.